Problemas de Dinámica del Punto (GITI)
Secciones
3.1. Cálculo de energías potenciales
Para las siguientes fuerzas, consideradas en una dimensión
- Peso: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle F = -mg}
- Elástica: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle F = -k(x-l_0)}
- Gravitatoria: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle F = -GMm/x^2}
- Determine la energía potencial de la que deriva cada una.
- Trace las curvas de potencial para las tres fuerzas.
- Considere el caso de una partícula sometida simultáneamente a una fuerza elástica y al peso, ¿cuál es la energía potencial como función de la posición? ¿Qué forma tiene su curva de potencial? ¿Qué movimiento describe una partícula sometida a estas dos fuerzas a la vez?
- Para el caso de la fuerza gravitatoria, calcule la velocidad de escape, definida como aquella que partiendo de la superficie de un planeta, permite llegar al infinito con velocidad nula.
3.2. Partícula sometida a fuerza dependiente de una coordenada (Ex.Ene/11)
Una partícula material de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} parte del origen de coordenadas con velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0=v_0\vec{\jmath}} , encontrándose sometida en todo momento a la fuerza dependiente de la posición
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}} la posición instantánea de la partícula, y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} dos constantes positivas conocidas.
- Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, .
- Demuestre que
- es una integral primera del movimiento de la partícula y calcule su valor en todo instante. ¿Qué significado físico tiene esta cantidad?
3.3. Tensión de un péndulo
Empleando el teorema de conservación de la energía mecánica, determine la velocidad con la que un péndulo simple de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} y longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle l_0} pasa por su punto más bajo, como función del ángulo máximo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta_0} con el que se separa de la vertical.
Determine la tensión de la cuerda en el punto más bajo y en el punto de máxima separación de la vertical.
3.4. Partícula en el interior de un aro
Se tiene un aro circular de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:
- Una anilla ensartada en el aro
- Una bolita que desliza por el interior del aro, sin estar unida a él.
Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
3.5. Partícula en el interior de un tubo
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano horizontal OXY girando con velocidad angular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \omega} constante alrededor del eje OZ, de forma que la posición de la partícula puede escribirse como
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho = \rho(t)\,} , función que hay que determinar, define la posición de la partícula a lo largo del tubo.
- Halle la ecuación diferencial que debe satisfacer Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho(t)\,} sabiendo que el tubo no puede ejercer fuerza en la dirección longitudinal (no hay rozamiento).
- Compruebe que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho(t) =A\mathrm{e}^{\omega t}\,} es una solución de dicha ecuación diferencial.
- Para esta solución particular
- Calcule la fuerza ejercida por el tubo en cada instante.
- Halle la potencia desarrollada por el tubo sobre la partícula.
- Calcule el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho = b\,} a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho = 2b\,} .
- Evalúe el incremento de energía cinética de la partícula en el mismo intervalo y compruebe que se verifica el teorema de la energía cinética.
3.6. Oscilador armónico en el plano
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} se encuentra sujeta a un resorte de constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula, el cual ejerce una fuerza
La posición inicial de la masa y su velocidad inicial son:
- Exprese el momento cinético de la partícula respecto al origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} y la energía mecánica de la partícula en función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z} y sus derivadas temporales, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{x}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{y}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{z}} .
- Demuestre que las dos magnitudes anteriores son integrales primeras y evalúelas en función de las condiciones iniciales.
- Demuestre que el movimiento de esta partícula se restringe al plano OXY y que su velocidad areolar respecto al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} es constante.
3.7. Integrales primeras en un helicoidal uniforme (Ex.Ene/12)
Una partícula P, de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , se mueve con respecto a un triedro cartesiano OXYZ siguiendo la ecuación horaria:
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b\,} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Omega\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_o\,} constantes conocidas.
- Determine las componentes intrínsecas de la aceleración de la partícula y el radio de curvatura de su trayectoria.
- Calcule la energía cinética de la partícula y la fuerza que causa el movimiento. Exprese y verifique matemáticamente la cualidad geométrica de la fuerza (condición de ortogonalidad) que guarda relación directa con el hecho de que la energía cinética sea integral primera.
- Determine el momento cinético de la partícula respecto al origen de coordenadas. ¿Se conserva constante en el tiempo alguna de las componentes cartesianas de dicho momento cinético? En caso afirmativo, explique por qué ocurre esto verificando matemáticamente que se cumple la condición necesaria establecida en el correspondiente teorema de conservación.
3.8. Movimiento bajo fuerza central en polares
Sea una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} cuyo movimiento en el plano OXY se describe mediante coordenadas polares.
- Deduzca la expresión de su velocidad areolar respecto al origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} , y compruebe que la misma es constante en el tiempo si el movimiento transcurre bajo la acción de una fuerza central en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} .
- Sabiendo que la partícula recorre la espiral Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho=\rho_{0}e^{\theta}\,} sometida a una fuerza central en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} y con condiciones iniciales Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(0)=0\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(0)=\omega_0} , determine las ecuaciones horarias Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho = \rho(t)\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta = \theta(t)\,} .
3.9. Sonda espacial
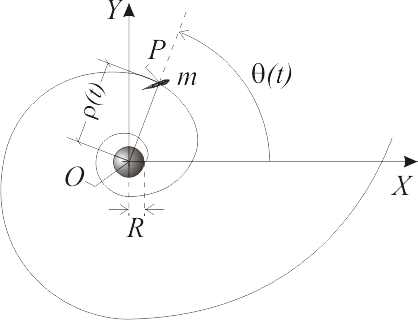
Una sonda espacial, considerada como un punto material Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , se mueve en el plano OXY (descrito mediante las coordenadas polares Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} de la figura) cuyo origen Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} coincide con el centro de un planeta de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} . Éste ejerce sobre la sonda una fuerza de atracción gravitatoria conservativa, cuya energía potencial asociada viene dada por la expresión:
Mediante la acción de sus motores, la sonda es puesta en órbita desde la superficie del planeta siguiendo la espiral logarítmica de ecuaciones horarias:
Despreciando las posibles fuerzas de fricción sobre la sonda, así como las pérdidas de masa asociadas al gasto de combustible, se pide:
- Deducir razonadamente si el movimiento de la sonda es o no es un movimiento central con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} .
- Comprobar que la energía cinética de la sonda responde a la expresión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K=C\rho^2\,} , determinando el valor de la constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C\,} en función de las constantes conocidas del problema.
- Aplicando el teorema de la energía mecánica, determinar el trabajo (no conservativo) realizado por los motores sobre la sonda durante el intervalo de tiempo que tarda ésta en duplicar su distancia inicial al centro del planeta.
3.10. Energía potencial lineal a tramos (Ex.Dic/11)
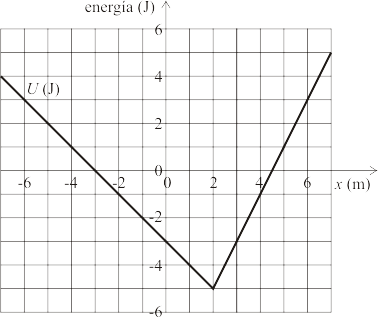
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m=1\,\mathrm{kg}} se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. En el instante inicial se encuentra en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=4\,\mathrm{m}} moviéndose en el sentido positivo del eje OX con celeridad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=2\,\mathrm{m/s}} .
- Halle la energía mecánica de la partícula.
- Se detiene en algún punto, ¿en cuál? Una vez que retorna, ¿dónde se vuelve a detener?
- Halle la fuerza sobre la partícula, así como su aceleración, en los dos puntos de retorno.
- ¿Qué tipo de movimiento describe la partícula entre cada punto de retorno y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=2\,\mathrm{m}} ?
- Suponga que la masa se ve sometida adicionalmente a una fuerza de rozamiento que la va frenando hasta detenerla por completo. ¿Dónde se detiene finalmente? ¿Cuánta energía mecánica se ha disipado desde el instante inicial hasta el instante en que la partícula se detiene definitivamente?
3.11. Partícula sujeta de dos hilos
Una masa m = 10 kg cuelga inicialmente de un hilo de 50 cm de longitud sujeto del techo a una distancia de 80 cm de la pared más cercana. Para evitar que el primer hilo se rompa, se afianza la masa sujetándola con un hilo adicional de 50 cm atado horizontalmente a la pared. Determine la tensión de cada hilo. ¿Ha aumentado o disminuido la tensión del hilo original?
3.12. Equilibrio de partícula en hélice
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada sin rozamiento en la hélice de ecuaciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = A\,\mathrm{cos}(\theta),} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y = A\,\mathrm{sen}(\theta),} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z = b\,\theta/(2\pi)} .
- Determine la posición de equilibrio de la partícula sobre la hélice.
- Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio.
- Determine la energía potencial como función del parámetro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} y discuta la estabilidad de la posición de equilibrio.
3.13. Partícula motorizada en aro (Ex.Ene/13)
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , está ensartada sin rozamiento en un aro fijo de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} , el cual se halla situado en el plano horizontal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} y tiene su centro en el origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} . Un motor ejerce una fuerza tangencial sobre la partícula, y como resultado ésta se mueve en sentido antihorario con una velocidad angular (escalar) que es función de la posición:
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K\,} es una constante positiva conocida, y el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} (definido en la figura) es el parámetro utilizado para describir la posición de la partícula sobre el aro.
- Determine la aceleración angular en función de la posición. ¿Qué tipo de movimiento circular realiza la partícula?
- Halle las componentes intrínsecas de la aceleración lineal en función de la posición.
- Calcule el trabajo que realiza el motor sobre la partícula al moverse ésta desde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=0\,} hasta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=(\pi/2)\,\mathrm{rad}\,} .
- Determine la fuerza de reacción vincular ejercida por el aro sobre la partícula para la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=(\pi/4)\,\mathrm{rad}\,} .
No Boletín - Cuatro bolitas ensartadas en un alambre liso (Ex.Ene/12)
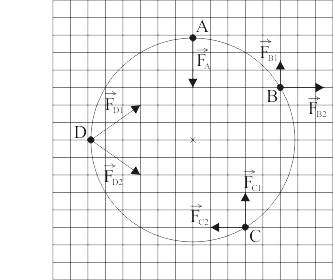
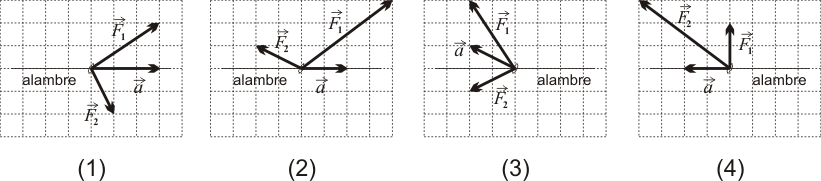
Las cuatro bolitas de la figura (A, B, C y D) se hallan ensartadas en un alambre liso con forma de circunferencia, pudiendo deslizar sin rozamiento a lo largo del mismo. Se han dibujado a escala todas las fuerzas activas soportadas por A, B, C y D para las posiciones dadas. Por el contrario, no se muestran en el gráfico las fuerzas de reacción vincular.
¿Qué bolitas se encuentran en una posición de equilibrio?
No Boletín - Cuestión sobre curva de potencial (Ex.Ene/12)
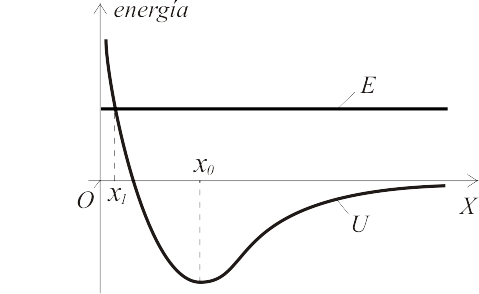
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} se mueve en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} bajo la acción de una fuerza conservativa cuya curva de energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U\,} es la representada (convergencia asintótica al nivel cero para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x\rightarrow\infty\,} ). La energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} de la partícula, también mostrada en la gráfica, es la recta horizontal que corta a la curva de energía potencial en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_1\,} . Sabemos que en cierto instante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=t_0\,} la partícula se encuentra en el punto de coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_0\,} , el cual corresponde a un mínimo de energía potencial.
¿Qué sabemos con certeza sobre el movimiento que realizará dicha partícula para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t>t_0\,} ? (NOTA: hay que elegir sólo una de las cuatro siguientes afirmaciones).
(a) Su celeridad para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\rightarrow\infty\,} será Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v=\sqrt{2E/m}\,.}
(b) Oscilará indefinidamente en torno a la posición de equilibrio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_0\,.}
(c) Permanecerá indefinidamente en la posición de equilibrio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_0\,.}
(d) Alcanzará la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_1\,} e invertirá el sentido de movimiento.
No Boletín - Cuestión sobre curva de potencial II (Ex.Ene/13)
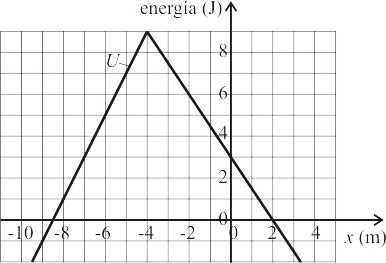
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1\,\mathrm{kg}\,} se mueve a lo largo del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} bajo la acción de una fuerza conservativa cuya energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U\,} es la representada en la gráfica. Sabemos que en el instante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=t_0\,} la partícula se halla en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_0=-8\,\mathrm{m}\,} y tiene una celeridad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0 = 2\,\mathrm{m/s}\,} en el sentido positivo del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} .
¿Cuál de las siguientes afirmaciones sobre el movimiento de la partícula para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t>t_0\,} es falsa? (NOTA: sólo una de las cuatro afirmaciones es falsa).
(a) Alcanzará un equilibrio inestable en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x= -4\,\mathrm{m}\,}
(b) Nunca pasará por la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = 1\,\mathrm{m}\,}
(c) En algún momento entrará en la región Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x<-8\,\mathrm{m}\,}
(d) Estará en reposo instantáneo en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = -7\,\mathrm{m}\,}
No Boletín - Cuestión sobre curva de potencial III (Ex.Ene/13)
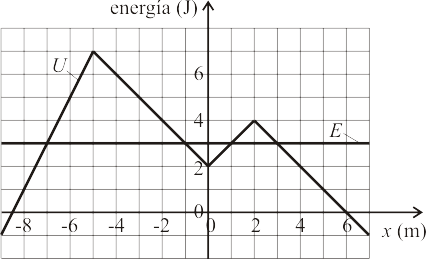
Una partícula material se mueve en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} bajo la acción de una fuerza conservativa cuya energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U\,} depende de la posición del modo que se indica en la gráfica. La energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} de la partícula vale Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3\,\mathrm{J}\,} .
Aun desconociendo su posición inicial, se puede asegurar con certeza que esta partícula en su movimiento ...
(a) ... pasa por tres posiciones de equilibrio.
(b) ... es imposible que alcance la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = -4\,\mbox{m}\,} .
(c) ... alcanza un único punto de retorno.
(d) ... oscila entre las posiciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = -1\,\mathrm{m}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = 1\,\mathrm{m}\,} .
Nota: Sólo es correcta una de las cuatro opciones.
No Boletín - Cuestión sobre curva de potencial IV (Ex.Jun/13)
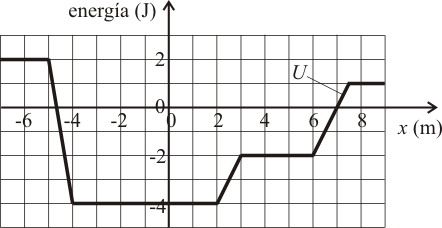
Una partícula de masa 1 kg se mueve sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} sometida exclusivamente a una fuerza conservativa cuya energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U\,} depende de la posición del modo que se indica en la gráfica. Se sabe que en el instante inicial la partícula tiene una celeridad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0= 2\,\mathrm{m/s}\,} y se halla en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_0 = 3\,\mathrm{m}\,} . ¿Cuánto vale la energía mecánica de la partícula? ¿Y la celeridad de la partícula en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x = -2\,\mathrm{m}\,} ?
No Boletín - Cuestión sobre curva de potencial V (Ex.Sep/14)

Una partícula se halla en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} sometida a la acción de una fuerza conservativa. La función energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U(x)\,} y el nivel de energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} de la partícula son los representados en la gráfica adjunta. ¿En qué posiciones está la partícula en reposo permanente?
No Boletín - Cuestión sobre curva de potencial VI (Ex.Ene/16)
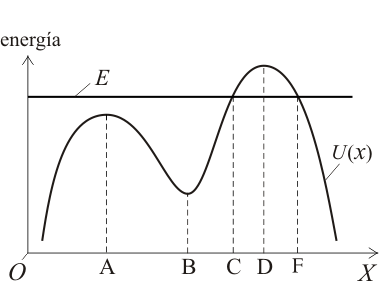
Una partícula material se mueve en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OX\,} bajo la única acción de una fuerza conservativa. En la gráfica adjunta se representan la energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} y la energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U(x)\,} de la partícula para cierta región de interés.
Aun desconociendo su posición inicial, se puede asegurar con certeza que esta partícula ...
(1) ... tiene accesibles tres posiciones de equilibrio (A, B y D).
(2) ... es imposible que alcance ninguna posición a la derecha de C.
(3) ... estará en reposo instantáneo si alcanza la posición F.
(4) ... estará en equilibrio si alcanza la posición C.
Nota: Sólo es correcta una de las cuatro opciones.
No Boletín - Cuestión sobre curva de potencial VII (Ex.Ene/20)
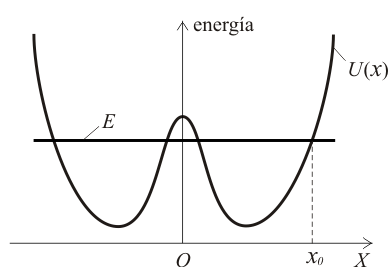
Una partícula se mueve en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OX\,} bajo la acción de una fuerza conservativa. La función energía potencial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U(x)\,} y el nivel de energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} de la partícula son los representados en la gráfica adjunta. La partícula se halla inicialmente en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,x=x_0\,} (ver gráfica), que corresponde a uno de los puntos de corte de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U(x)\,} .
¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento?
No Boletín - Cuestión sobre integral primera (Ex.Ene/13)
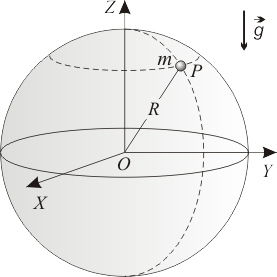
En el sistema de referencia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXYZ\,} de la figura, la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} se mueve bajo la acción de su propio peso y vinculada sin rozamiento a una superficie esférica fija de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} y centro en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} (la ecuación de ligadura es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x^{2}+y^{2}+z^{2}=R^{2}\,} ).
¿Cuál de las siguientes magnitudes físicas de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} se conserva necesariamente constante durante el movimiento? (NOTA: sólo una de las cuatro opciones es correcta).
(a) La componente-Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z\,} de su momento cinético respecto al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,}
(b) Su cantidad de movimiento
(c) Su energía cinética
(d) Su momento cinético respecto al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,}
No Boletín - Cuestión sobre integral primera II (Ex.Ene/15)
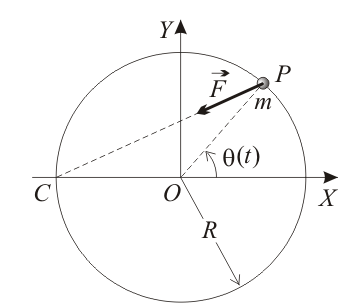
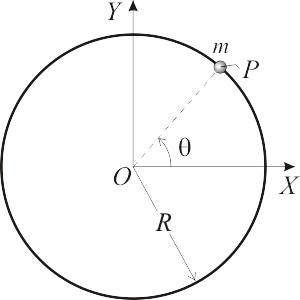
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} se mueve en el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} . Su trayectoria es la circunferencia de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} y centro en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O(0,0)\,} . La partícula soporta una única fuerza Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}\,} , cuya recta de acción pasa permanentemente por el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C(-R,0)\,} . Como parámetro descriptivo del movimiento, se utiliza el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(t)\,} de la figura, que satisface las condiciones iniciales Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(0)=0\,\,\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\,\dot{\theta}(0)=\Omega\,} .
- Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}\,}
es la velocidad instantánea de la partícula, ¿cuál de las siguientes magnitudes es una integral primera del movimiento de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,\,}
? (NOTA: sólo lo es una de las cuatro).
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{(a)}\,\,\,\, m\,\vec{v}\cdot\vec{v}/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(b)}\,\,\,\, \overrightarrow{OP}\times m\vec{v}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(c)}\,\,\,\, \overrightarrow{CP}\times m\vec{v}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(d)}\,\,\,\, m\vec{v}} - A partir de la integral primera del apartado anterior, deduzca la relación existente entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} durante el movimiento.
No Boletín - Cuestión sobre reacción vincular de alambre rectilíneo liso (Ex.Ene/15)
Una anilla, de dimensiones despreciables (considérese puntual) y de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2\,\,\mathrm{kg}\,} , desliza sin rozamiento a lo largo de un alambre rectilíneo en el que se halla ensartada. En cierto instante, se ha representado gráficamente la posición de la anilla, así como su aceleración (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{a}\,\,} ) y todas las fuerzas activas que soporta (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_1\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_2\,} ). Sin embargo, se ha dejado sin representar la fuerza de reacción vincular (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}\,} ) que ejerce el alambre liso sobre la anilla. La cuadrícula de los diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial.
¿Cuál de los siguientes diagramas es el correcto?
No Boletín - Cuestión sobre reacción vincular de aro liso (Ex.Feb/14)
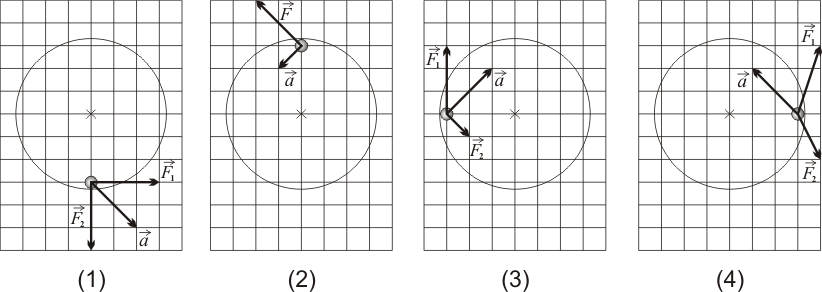
Una partícula material, de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1\,\,\mathrm{kg}\,} , desliza sin rozamiento por el interior de un aro circular. En cierto instante, se ha representado gráficamente la posición de la partícula, así como su aceleración y todas las fuerzas activas que soporta. Sin embargo, se ha dejado sin representar la fuerza de reacción vincular que ejerce el aro liso sobre la partícula. La cuadrícula de los diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial.
¿Cuál de los siguientes diagramas es el correcto?
No Boletín - Ecuaciones horarias en coordenadas polares (Ex.Feb/14)
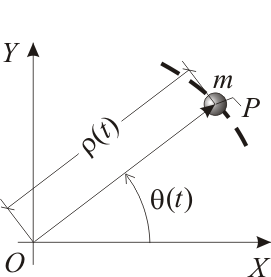
El movimiento de una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , en el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} queda descrito en coordenadas polares mediante las ecuaciones horarias:
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Omega\,} constantes positivas conocidas.
- Determine la velocidad y la aceleración de la partícula en componentes polares.
- Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria.
- Calcule la energía cinética de la partícula, y la potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula.
- ¿Es el movimiento de la partícula un movimiento central con centro en el origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} ? Razone la respuesta.
No Boletín - Ecuaciones horarias en coordenadas polares II (Ex.Ene/16)
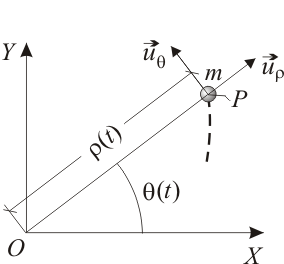
El movimiento de una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,m\,} , en el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OXY\,} queda descrito en coordenadas polares mediante las ecuaciones horarias:
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\rho_0\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,c\,} constantes positivas conocidas.
- Determine la velocidad y la aceleración de la partícula (en la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\{\vec{u}_{\rho},\vec{u}_{\theta}\}\!\,} ).
- Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria.
- Determine los vectores Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\overrightarrow{T}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\overrightarrow{N}\,} del triedro intrínseco de la trayectoria de la partícula (en la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\{\vec{u}_{\rho},\vec{u}_{\theta}\}\!\,} ).
- Calcule la energía cinética de la partícula, y la potencia desarrollada por la fuerza neta que actúa sobre ella. ¿Es la energía cinética una integral primera del movimiento?
- Calcule el momento cinético de la partícula respecto al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O.\,} ¿Es el movimiento de la partícula un movimiento central con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O\,} ? Razone la respuesta.
No Boletín - Equilibrio de partícula en parábola
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte de constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula anclado en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_0=\vec{0}} . La partícula está ensartada en la parábola Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y=0} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z = -x^2/(2b)} .
- Determine la(s) posición(es) de equilibrio de la masa sobre la parábola.
- Calcule la fuerza de reacción vincular de la parábola sobre la partícula en la(s) posición(es) de equilibrio.
- Trace la curva de la energía potencial como función de la coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} y discuta la estabilidad de las posibles posiciones de equilibrio.
No Boletín - Fuerza neta sobre un vehículo en una curva (Ex.Sep/15)
Un vehículo (masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} ) está saliendo de una curva, y su celeridad (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v=|\vec{v}\,|\,} ) está aumentando. ¿Cuál de los siguientes diagramas representa correctamente la dirección y el sentido de la fuerza neta (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}\,} ) que actúa sobre dicho vehículo?
No Boletín - Movimiento central en coordenadas polares (Ex.Dic/12)
El movimiento de una partícula en un plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} (para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t>0\,} ) viene dado en coordenadas polares mediante las ecuaciones horarias:
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C_1\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C_2\,} son constantes conocidas. Sabiendo que la fuerza que actúa sobre la partícula es central con centro en el origen de coordenadas, ¿cuál es necesariamente el valor del exponente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n\,} ?
No Boletín - Movimiento rectilíneo por tramos
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} , realiza un movimiento rectilíneo sobre la parte positiva de un eje cartesiano OX. Cuando la distancia entre la partícula y el origen Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} supera una cierta longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b} conocida, la partícula es atraída hacia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} por una fuerza de módulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle mk/x^2} (siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} una constante); pero, sin embargo, cuando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x<b} , la partícula es repelida desde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} por una fuerza de módulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle mbk/x^3} .
- Determine y represente gráficamente la energía potencial de la partícula en función de su coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} (considerando que dicha función es nula en el infinito y exigiendo su continuidad en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=b} ).
- Sabiendo que la partícula inicia su movimiento desde el reposo instantáneo en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_0} de coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=2b} , determine su energía mecánica.
- ¿En qué otro punto alcanzará la partícula el reposo instantáneo (punto de retorno)?
No Boletín - Muelle en plano inclinado (Ex.Nov/10)
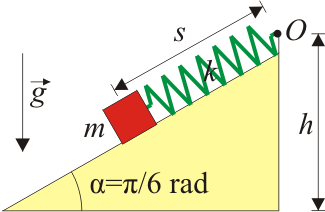
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} se halla inicialmente en reposo a una altura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h} (punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} ). La partícula comienza a deslizar sin rozamiento sobre un plano inclinado un ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha = \pi/6\,} rad, bajo la acción de su propio peso y manteniéndose conectada con el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} mediante un resorte de constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula.
- ¿Qué distancia recorre la partícula hasta que se para por primera vez?
- Cuando la partícula se encuentra a una distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle s} de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} , ¿cuánto vale el módulo de la fuerza de reacción vincular?
No Boletín - Muelle en plano inclinado II (Ex.Ene/19)
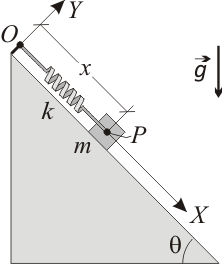
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , desliza sin rozamiento a lo largo de una rampa de inclinación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} respecto a la horizontal. Durante su movimiento, la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} está sometida a la acción de su propio peso y es solicitada desde un punto fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} (ver figura) mediante un resorte elástico Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OP\,} de constante recuperadora Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} y longitud natural Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle l_0\,} . Se describe la posición de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} mediante su coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x\,} en la escuadra Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} de la figura.
- ¿Cuánto vale la fuerza vincular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}\,} que la rampa ejerce sobre la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} ?
- ¿Qué ecuación diferencial satisface la función Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)\,} que describe la posición de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} en cada instante?
- ¿Cuál es la posición de equilibrio de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} ?
No Boletín - Partícula cae por rampa e impacta en muelle (Ex.Sep/12)
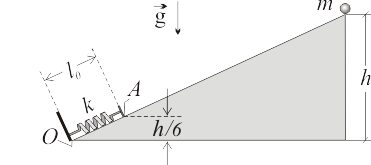
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} desliza sin rozamiento a lo largo de una rampa bajo el efecto de su propio peso. En el instante inicial, la partícula se halla en reposo en el punto más alto de la rampa, a una altura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h\,} . Al final de la rampa y apoyado sobre ella, hay un resorte elástico OA de constante recuperadora Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} y longitud natural Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle l_0\,} . Su extremo O está fijo (punto de anclaje), y su extremo libre A descansa sobre la rampa, a una altura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h/6\,} cuando el resorte está relajado.
- ¿Con qué celeridad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v\,} entrará en contacto la partícula con el extremo A del resorte?
- ¿Cuánto vale la constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} del resorte si la partícula llega hasta el final de la rampa (punto O) con celeridad nula?
No Boletín - Partícula colgada de dos hilos (Ex.Dic/11)
Una partícula de peso 300 N cuelga de un techo horizontal sujeta por dos hilos ("1" y "2"). El hilo "1" forma un ángulo de 30º con la vertical, mientras que el hilo "2" forma uno de 60º con la vertical. ¿Cuánto valen, en módulo, las tensiones de los dos hilos?
No Boletín - Partícula en aro (Ex.Sep/15)
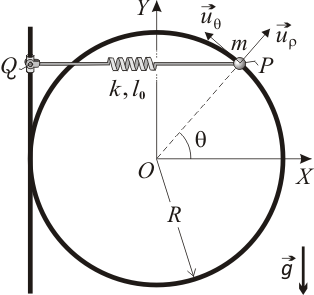
En el plano vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OXY\,} (gravedad: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{g}=-g\,\vec{\jmath}\,} ) se halla una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,m\,} , ensartada sin rozamiento en un aro fijo de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,R\,} y centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} . Dicha partícula está conectada a una guía vertical fija (de ecuación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,x=-R\,} ) mediante un resorte elástico Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,QP\,} de constante recuperadora Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,k=2mg/R\,} y longitud natural Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,l_0=R.\,} El extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,Q\,} se desplaza sobre la citada guía de tal modo que el resorte Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,QP\,} permanece en todo instante paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX.\,}
Se propone la coordenada acimutal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta\,} (definida en la figura) para describir la posición de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,P\,} , así como la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\{\vec{u}_{\rho},\vec{u}_{\theta}\}\,} para expresar las magnitudes vectoriales.
- Plantee la segunda ley de Newton para la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} en la base polar y, separando componentes, obtenga: (a) La ecuación diferencial de segundo orden que debe satisfacer la función Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta(t).\,} (b) La fuerza de reacción vincular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{\Phi}(\theta,\dot{\theta})\,} que ejerce el aro sobre la partícula.
- Deduzca razonadamente (mediante algún teorema de conservación) una integral primera del movimiento de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,P\,} , exprésela como una función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\dot{\theta}\,} , y determine su valor constante para el supuesto de que la partícula se encuentre inicialmente en reposo en la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta=0.\,}
- Halle todas las posiciones de equilibrio mecánico de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,P\,} , y clasifíquelas según correspondan a equilibrio estable o inestable.
No Boletín - Partícula en semicircunferencia (Ex.Dic/12)
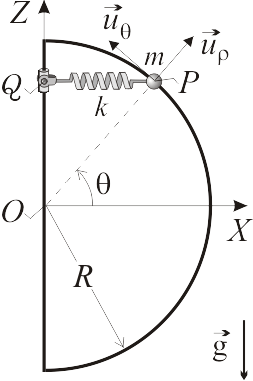
En el plano vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXZ\,} (gravedad: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{g}=-g\,\vec{k}\,} ), se halla una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , ensartada sin rozamiento en la semicircunferencia fija, de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} , que se muestra en la figura. Dicha partícula es solicitada desde el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OZ\,} por un resorte elástico Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle QP\,} , de constante recuperadora Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k=2mg/R\,} y longitud natural nula. El extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q\,} se puede desplazar sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OZ\,} , de tal modo que el resorte permanece en todo instante paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} .
Utilizando la coordenada acimutal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} para describir la posición de la partícula, y la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_{\rho}, \vec{u}_{\theta}\}\,} para expresar las magnitudes vectoriales, se pide:
- Determinar la posición de equilibrio existente en el intervalo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\pi/2<\theta<\pi/2\,} , así como la fuerza de reacción vincular que soportaría la partícula si se hallase en equilibrio en dicha posición.
- Expresar la energía potencial de la partícula como una función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} , y discutir si la posición de equilibrio del apartado anterior es estable o inestable.
- Deducir razonadamente (mediante algún teorema de conservación) una integral primera del movimiento de la partícula, expresarla como una función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}\,} , y determinar su valor constante para el caso en que las condiciones iniciales sean: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(0)=-\pi/2\,} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(0)=\sqrt{2g/R}\,} .
No Boletín - Partícula en varilla ranurada móvil (Ex.Ene/20)
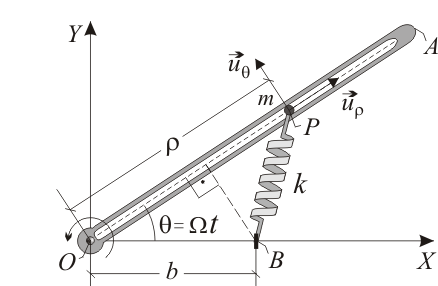
La varilla Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OA\,} , ranurada longitudinalmente y contenida en el plano horizontal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} , rota alrededor del eje fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OZ\,} de tal modo que el ángulo que forma la misma con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} viene dado en función del tiempo por la expresión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta=\Omega\, t\,} (donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\Omega\,} es una constante conocida). Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} se encuentra confinada en la ranura de la citada varilla, pudiendo deslizar sin rozamiento a lo largo de ella, y estando sometida a la acción de un resorte elástico (de constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} y longitud natural nula) con anclaje en el punto fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B(b,0,0)\,} . En la figura se definen las coordenadas polares Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\rho,\theta\}\,} de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , así como la base ortonormal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_{\rho},\vec{u}_{\theta}\}\,} asociada a las mismas. En lo que sigue, denominaremos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}\,} , respectivamente, a la velocidad y a la aceleración de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} respecto al triedro fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXYZ\,} .
Nota: Obsérvese que la varilla Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OA\,} constituye un vínculo liso y reónomo sobre la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} .
- ¿Cuál de las siguientes condiciones ha de ser verificada en todo instante por la fuerza vincular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}\,}
que ejerce la varilla Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OA\,}
sobre la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,}
?
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{(1)}\,\,\,\vec{\Phi}\cdot\vec{u}_{\theta}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(2)}\,\,\,\vec{\Phi}\cdot\vec{v}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(3)}\,\,\,\vec{\Phi}\cdot\vec{u}_{\rho}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(4)}\,\,\,\vec{\Phi}\times\vec{a}=\vec{0}} - Proyectando la segunda ley de Newton sobre la dirección radial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_{\rho}\,} , deduzca la ecuación diferencial que debe satisfacer la función Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho(t)\,} que da la coordenada radial de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} en cada instante.
- ¿Cuál de las siguientes magnitudes físicas conserva su valor constante durante el movimiento de la partícula?
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{(1)}\,\,\,\mathrm{ninguna}\,\,\mathrm{de}\,\,\mathrm{las}\,\,\mathrm{otras}\,\,\mathrm{tres}\,\,\,\,\,\,\,\,\mathrm{(2)}\,\,\,(m\,\vec{v}\,\cdot\,\vec{v}\,+\,k\,\overrightarrow{BP}\,\cdot\,\overrightarrow{BP}\,)/2\,\,\,\,\,\,\,\,\mathrm{(3)}\,\,\,\overrightarrow{BP}\,\times\, m\,\vec{v}\,\,\,\,\,\,\,\,\mathrm{(4)}\,\,\,m\,\vec{v}\,\cdot\,\vec{v}/2}
No Boletín - Partícula motorizada en hélice (Ex.Ene/15)
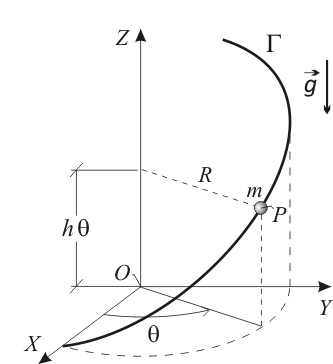
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , se encuentra ensartada sin rozamiento en la hélice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Gamma\,} de la figura. Esto permite que la posición de la partícula (respecto al triedro cartesiano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXYZ\,} ) pueda describirse mediante las ecuaciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} -paramétricas de dicha hélice vincular:
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h\,} son constantes positivas conocidas.
Además de soportar la acción gravitatoria (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\vec{g}\,} ) y la fuerza de reacción vincular (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}\,} ) ejercida por la hélice lisa, la partícula es empujada en sentido ascendente por una fuerza motora tangente al vínculo (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{\mathrm{mot}}=F_{\mathrm{mot}}\overrightarrow{T}\,} ). Como resultado de todo ello, la partícula sube a lo largo de la hélice con celeridad constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0\,} , partiendo en el instante inicial (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,} ) desde la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=0\,} .
- Halle la ley horaria Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(t)\,} con la que la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} recorre la hélice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Gamma\,} .
- Calcule (en función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} ) las componentes tangencial y normal de la aceleración de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , así como los vectores tangente unitario y normal principal del triedro intrínseco de su trayectoria.
- Proyectando la ecuación de la segunda ley de Newton sobre la dirección tangente a la hélice, determine el módulo de la fuerza motora (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle F_{\mathrm{mot}}\,} ) que actúa sobre la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} . ¿Qué trabajo total realiza dicha fuerza motora entre el instante inicial y el instante en el que la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} alcanza la posición Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=2\pi\,} ?
- Calcule la componente vertical del momento cinético de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} respecto al origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} , y explique por qué dicha componente resulta independiente del tiempo.
No Boletín - Partícula que cuelga de un hilo (Ex.Sep/14)
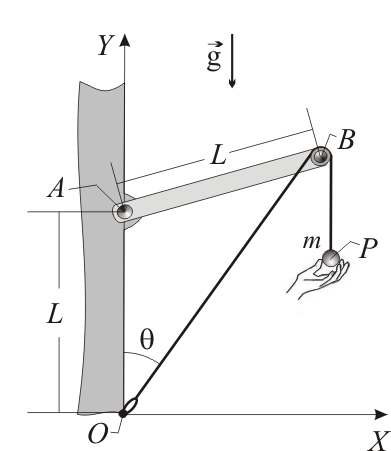
La barra rígida Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB\,} -de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle L\,} y masa despreciable- se mueve en el plano vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} , hallándose articulada en su extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} a un punto del eje vertical cuya posición es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OA}= L\vec{\jmath}\,} . Un hilo inextensible de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2L\,} tiene uno de sus extremos fijo en el origen del sistema de coordenadas (punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} ), mientras que del otro extremo cuelga una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} . El hilo se mantiene siempre tenso, se apoya sobre una pequeña polea de radio despreciable situada en el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B\,} de la barra, y en su tramo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overline{BP}\,} permanece en todo instante paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY\,} (ver figura). Como parámetro auxiliar descriptivo de la posición del sistema, se define el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} que forman el tramo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overline{OB}\,} del hilo y el eje vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY\,} (considérese Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\leq\theta<\pi/2\,} ).
- Halle razonadamente el vector de posición de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OP}\,} en función del parámetro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} , así como la velocidad instantánea de la misma en función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}\,} .
- Suponga que se verifica la ley horaria Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(t) = \Omega t\,}
(donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Omega\,}
es una constante positiva conocida). Sabiendo que en tal caso la velocidad instantánea de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,}
viene dada por:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}(t)=C\left\{\mathrm{cos}(2\Omega t)\,\vec{\imath}-[\mathrm{sen}(2\Omega t)+\,\mathrm{sen}(\Omega t)]\,\vec{\jmath}\,\right\}} donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C\,} es otra constante positiva conocida, determine las componentes intrínsecas (tangencial y normal) de la aceleración de la partícula en el instante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=\pi/(4\Omega)\,} , así como el trabajo neto realizado sobre la partícula en el intervalo de tiempo transcurrido entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=\pi/(3\Omega)\,} . - Suponga que la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} realiza el movimiento descrito en el apartado anterior bajo la acción de tres fuerzas: su propio peso, la fuerza que le ejerce el hilo y una fuerza aplicada con la mano (esta última es necesaria para garantizar que el hilo permanezca siempre tenso y con su tramo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overline{BP}\,} vertical). Calcule la componente horizontal de la fuerza aplicada con la mano en función del tiempo.
No Boletín - Partícula que desliza apoyada sobre semiaro (Ex.Ene/16)
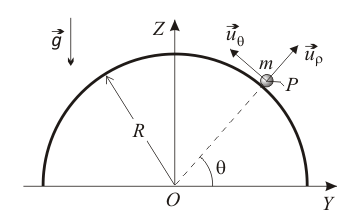
Sea un semiaro fijo, de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,R\,} y centro de curvatura Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O\,} , contenido en el plano vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OY\!Z\,} (ver figura). La partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,m\,} , inicialmente en reposo apoyada sobre el punto más alto del semiaro, sufre una leve perturbación y comienza a deslizar sobre él sin rozamiento y bajo la acción de su propio peso (aceleración gravitatoria: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{g}=-g\,\vec{k}\,} ). El deslizamiento continúa hasta cierta posición en la que se observa que la partícula pierde el contacto con el semiaro. Utilícese la coordenada acimutal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\theta\,} de la figura para describir la posición de la partícula sobre el semiaro, y la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_{\rho},\vec{u}_{\theta}\}\,} para expresar las magnitudes vectoriales.
- Halle la celeridad de la partícula mientras desliza sobre el semiaro.
- Determine la fuerza de reacción vincular que el semiaro ejerce sobre la partícula durante su deslizamiento.
- ¿En qué posición pierde la partícula el contacto con el semiaro?
No Boletín - Partícula sujeta por dos hilos realizando un m.c.u. (Ex.Feb/17)
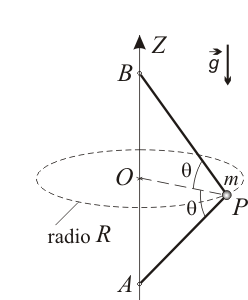
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , describe con celeridad constante una circunferencia horizontal de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} y centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} . La partícula realiza dicho movimiento circular y uniforme bajo la acción de su propio peso (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\vec{g}\,} ) y de las dos fuerzas (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}_{A}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}_{B}\,} ) que le ejercen, respectivamente, sendos hilos tensos de idéntica longitud y anclados en los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B\,} del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OZ\,} (puntos equidistantes del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} ).
Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} el ángulo que forma cada uno de los dos hilos con el plano horizontal durante el movimiento de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} (ver figura).
Se sabe que el módulo de la fuerza ejercida por el hilo superior (el anclado en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B\,} ) es el cuádruple del módulo de la fuerza ejercida por el hilo inferior (el anclado en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} ):
Se pide:
- El módulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\vec{\Phi}_{A}|\,} de la fuerza ejercida por el hilo inferior.
- El módulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\,\vec{\omega}\,|\,} de la velocidad angular de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} .
No Boletín - Partícula unida a dos muelles (Ex.Feb/14)
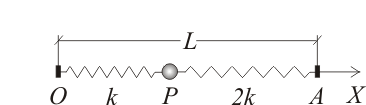
Una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , se mueve en el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX\,} sometida exclusivamente a las fuerzas que ejercen sobre ella dos resortes elásticos ideales. Ambos resortes tienen longitud natural nula, pero uno de ellos (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OP\,} ) está anclado en el origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} y tiene constante elástica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} , mientras que el otro (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AP\,} ) está anclado en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} de coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_{_{\! A}}\!=L\,\,} y tiene constante elástica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2k\,} .
- ¿Cuál es la posición de equilibrio?
- ¿Qué celeridad máxima alcanzará la partícula en su movimiento si en el instante inicial se halla en reposo en el punto medio entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} ?
No Boletín - Partícula unida a un muelle (Ex.Sep/14)
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} se halla sujeta al extremo de un muelle cuyo otro extremo permanece fijo. El muelle tiene constante elástica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k\,} y, bajo su acción exclusiva, la partícula realiza un movimiento armónico simple. ¿Qué relación existe entra la celeridad máxima Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_{\mathrm{max}}\,} que alcanza la partícula durante el movimiento y la amplitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} de su oscilación?
No Boletín - Péndulo cónico (Ex.Ene/13)
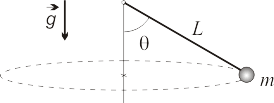
Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , la longitud del péndulo es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle L\,} , el ángulo que forma el hilo con la vertical es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} y la gravedad es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle g\,} .
- ¿Con qué celeridad se mueve la masa puntual?
- ¿Cuál es el módulo de la tensión del hilo?
No Boletín - Péndulo simple (Ex.Ene/18)

Considérese un péndulo simple, constituido por una partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} (de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} ) que se halla suspendida de un punto fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} mediante un hilo inextensible (de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle L\,} y masa despreciable). Bajo la acción de su propio peso, la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} oscila en el plano vertical fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OXY\,} (aceleración gravitatoria: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{g}=g\,\vec{\imath}\,} ). Se propone la coordenada acimutal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} (definida en la figura) para describir la posición de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} , así como la base polar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_{\rho},\vec{u}_{\theta}\}\,} para expresar las magnitudes vectoriales.
- De la segunda ley de Newton aplicada a la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} y proyectada sobre la dirección acimutal, deduzca la ecuación diferencial de segundo orden que debe satisfacer la función Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta(t)\,} .
- Y de la misma ley, pero proyectada sobre la dirección radial, deduzca el módulo de la tensión del hilo.
- Deduzca una integral primera del movimiento de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} aplicando algún teorema de conservación.
No Boletín - Velocidad y tipo de movimiento a partir de la fuerza (Ex.Dic/12)
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , inicialmente en reposo en el origen de coordenadas, soporta la acción de una única fuerza:
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B\,} son dos constantes conocidas.
- Determine la velocidad instantánea de la partícula.
- ¿Qué tipo de movimiento realiza la partícula?