No Boletín - Cuestión sobre curva de potencial (Ex.Ene/12)

Enunciado

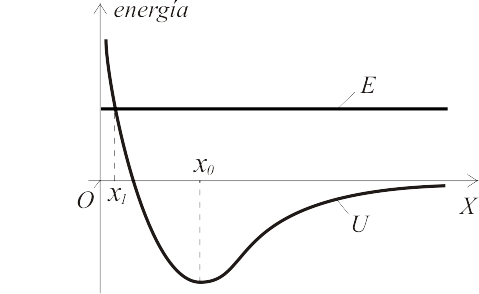
Una partícula de masa $m\,$ se mueve en el eje $OX\,$ bajo la acción de una fuerza conservativa cuya curva de energía potencial $U\,$ es la representada (convergencia asintótica al nivel cero para $x\rightarrow \infty \,$). La energía mecánica $E\,$ de la partícula, también mostrada en la gráfica, es la recta horizontal que corta a la curva de energía potencial en $x=x_{1}\,$. Sabemos que en cierto instante $t=t_{0}\,$ la partícula se encuentra en el punto de coordenada $x=x_{0}\,$, el cual corresponde a un mínimo de energía potencial.

¿Qué sabemos con certeza sobre el movimiento que realizará dicha partícula para $t>t_{0}\,$? (NOTA: hay que elegir sólo una de las cuatro siguientes afirmaciones).

(a) Su celeridad para $t\rightarrow \infty \,$ será $v={\sqrt {2E/m}}\,.$

(b) Oscilará indefinidamente en torno a la posición de equilibrio $x=x_{0}\,.$

(c) Permanecerá indefinidamente en la posición de equilibrio $x=x_{0}\,.$

(d) Alcanzará la posición $x=x_{1}\,$ e invertirá el sentido de movimiento.

Descartando la opción (c)

El punto de coordenada $x=x_{0}\,$ corresponde a un mínimo de energía potencial y, por tanto, es una posición de equilibrio estable. Sin embargo, el nivel de energía mecánica $E\,$ de la partícula es mayor que $U(x_{0})\,$, y esto implica que la partícula, cuando se halla en $x=x_{0}\,$, tiene energía cinética no nula:

$\mathrm {para} \,\,\,x=x_{0}\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\frac {1}{2}}m{\dot {x}}^{\,2}=K=E-U(x_{0})>0\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\dot {x}}>0$

Es decir, la partícula no está en reposo en la posición $x=x_{0}\,$ y, por tanto, no se quedará allí. El reposo permanente de una partícula en una posición exige aceleración nula (que sí la tiene en la posición de equilibrio), pero también exige velocidad nula (que es lo que en este caso no tiene en $x=x_{0}\,$). Queda descartada, pues, la opción (c).

Cabe señalar que la opción (c) habría sido correcta si el nivel de energía mecánica $E\,$, en lugar de ser el que se muestra en la gráfica, hubiese sido $E=U(x_{0})\,.$

Descartando la opción (b)

En la gráfica observamos la existencia de un único punto de corte (en $x=x_{1}\,$) de la curva $U(x)\,$ y la recta horizontal $E\,$. Por tanto, $x=x_{1}\,$ es el único punto de retorno:

$\mathrm {para} \,\,\,x=x_{1}\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\frac {1}{2}}m{\dot {x}}^{\,2}=K=E-U(x_{1})=0\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\dot {x}}=0$

La partícula tiene prohibido el acceso a la región $x<x_{1}\,$ (eso implicaría energía cinética negativa), pero cuando se mueva hacia la derecha (es decir, cuando tenga ${\dot {x}}>0\,$) no encontrará punto de retorno alguno y avanzará indefinidamente hacia $x\rightarrow \infty \,$. Por eso sabemos que no oscilará indefinidamente en torno a la posición de equilibrio $x=x_{0}\,$. Queda, por tanto, también descartada la opción (b).

Cabe comentar que la opción (b) habría sido correcta si el nivel de energía mecánica $E\,$, en lugar de ser el que se muestra en la gráfica, hubiese sido tal que $U(x_{0})<E<0\,$. En ese caso habría existido un segundo punto de retorno a la derecha de $x=x_{0}\,$, la partícula estaría confinada en un pozo de potencial y oscilaría indefinidamente en torno a la posición de equilibrio.

Descartando la opción (d)

Dice la opción (d): "Alcanzará la posición $x=x_{1}\,$ e invertirá el sentido de movimiento". E invertir el sentido de movimiento es ciertamente algo que hace la partícula cuando alcanza un punto de retorno. Siendo -como lo es- $x=x_{1}\,$ un punto de retorno, esta opción parece correcta, pero... ¿tenemos certeza de que la partícula va a alcanzar este punto de retorno para $t>t_{0}\,$? Para que así fuera, haría falta que en el instante $t=t_{0}\,$ la partícula se estuviese moviendo hacia la izquierda, es decir, que ${\dot {x}}(t_{0})<0\,$. El enunciado nos dice que $x(t_{0})=x_{0}\,$ pero nada nos dice acerca del signo de ${\dot {x}}(t_{0})\,$. Por tanto, no tenemos certeza de que la partícula vaya a alcanzar la posición $x=x_{1}\,$ para $t>t_{0}\,$, y por ello tenemos que descartar también la opción (d).

Como queda dicho en el párrafo anterior, la opción (d) habría sido correcta si hubiésemos sabido por el enunciado que ${\dot {x}}(t_{0})<0\,$.

Eligiendo la opción (a)

La opción (a) es la única correcta. Afirma que la celeridad de la partícula para $t\rightarrow \infty \,$ será $v={\sqrt {2E/m}}\,$. Es evidente que la partícula, antes o después, está "condenada" a alejarse indefinidamente hacia la derecha. Puesto que desconocemos el signo de ${\dot {x}}(t_{0})\,$, no sabemos si viajará directamente hacia la derecha después de $t=t_{0}\,$ (caso ${\dot {x}}(t_{0})>0\,$), o si previamente viajará hacia la izquierda al encuentro del punto de retorno $x=x_{1}\,$ y posteriormente comenzará su viaje "sin retorno" hacia la derecha (caso ${\dot {x}}(t_{0})<0\,$). Pero, en cualquiera de los dos casos, lo cierto es que:

$\lim _{t\rightarrow \infty }x(t)=\infty$

Y sabiendo que la coordenada $x\,$ de la partícula va a crecer indefinidamente cuando $t\rightarrow \infty \,$, ya podemos deducir el valor límite hacia el que va a tender la energía cinetíca, y el correspondiente valor de la celeridad de la partícula:

$\mathrm {para} \,\,\,t\rightarrow \infty \,\,\,\,\,\Longrightarrow \,\,\,\,\,x\rightarrow \infty \,\,\,\,\,\Longrightarrow \,\,\,\,\,{\frac {1}{2}}m{\dot {x}}^{\,2}=K=E-\underbrace {U(x\rightarrow \infty )} _{\displaystyle =0}=E\,\,\,\,\,\Longrightarrow \,\,\,\,\,v={\dot {x}}={\sqrt {2E/m}}$