No Boletín - Cuatro bolitas ensartadas en un alambre liso (Ex.Ene/12)

Enunciado

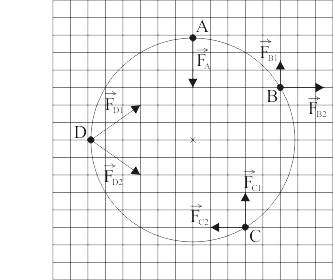
Las cuatro bolitas de la figura (A, B, C y D) se hallan ensartadas en un alambre liso con forma de circunferencia, pudiendo deslizar sin rozamiento a lo largo del mismo. Se han dibujado a escala todas las fuerzas activas soportadas por A, B, C y D para las posiciones dadas. Por el contrario, no se muestran en el gráfico las fuerzas de reacción vincular.

¿Qué bolitas se encuentran en una posición de equilibrio?

Solución

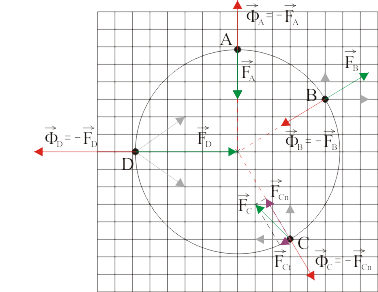
Al haberse dibujado a escala -sobre la cuadrícula de la figura- todas las fuerzas activas soportadas por A, B, C y D, estamos en condiciones de poder calcular (mediante suma vectorial gráfica) la resultante de fuerzas activas que actúa sobre cada una de las bolitas. Al hacerlo, hallamos que dichas resultantes (en color verde) son todas normales al alambre (es decir, radiales) excepto la correspondiente a la bolita C.

Sabemos que la condición de equilibrio mecánico para una posición consiste en la nulidad de la resultante de todas las fuerzas (activas y de reacción vincular) que actúan sobre la partícula. Es cierto que no se muestran en el gráfico del enunciado las fuerzas de reacción vincular, pero sabemos que el vínculo es liso (no hay rozamiento), es decir, que el alambre sólo puede ejercer fuerzas de reacción vincular normales.

La conclusión es inmediata. Se hallan en posiciones de equilibrio las bolitas A, B y D, ya que sus respectivas resultantes de fuerzas activas, al ser normales al alambre, pueden ser completamente neutralizadas por las correspondientes fuerzas de reacción vincular (en color rojo). Así, si dichas bolitas se colocasen en reposo inicial en sus respectivas posiciones, el alambre impediría el movimiento ejerciendo sobre cada una de ellas una fuerza de reacción vincular opuesta a la correspondiente resultante de fuerzas activas.

Por el contrario, la posición ocupada por C no es de equilibrio, ya que el alambre (al ser liso) es incapaz de ejercer la fuerza de reacción vincular tangencial necesaria para neutralizar a la componente tangencial de la resultante de fuerzas activas. En la figura adjunta, la resultante de fuerzas activas sobre C se ha descompuesto en sus componentes normal y tangencial al vínculo (en color morado), y podemos observar cómo la fuerza de reacción vincular es opuesta a la componente normal de la resultante de fuerzas activas pero no neutraliza a la componente tangencial.

¿Y si las bolitas no estuviesen ensartadas, sino apoyadas sobre la parte externa del alambre?

En un examen de Enero/2018 se planteó una cuestión parecida a la que acabamos de resolver, pero con la diferencia de que las bolitas no estaban ensartadas (vínculo bilateral) sino apoyadas sobre la parte externa del alambre (vínculo unilateral). Parece interesante por ello plantearnos cuál habría sido la respuesta correcta a la presente cuestión en tal supuesto.

Si las bolitas se hallasen apoyadas sobre la parte externa del alambre liso, éste sólo tendría la capacidad de ejercer fuerza de reacción vincular normal en el sentido hacia fuera. Por tanto, en tal supuesto sólo se hallarían en posiciones de equilibrio las bolitas A y D, ya que sus respectivas resultantes de fuerzas activas son normales al alambre y con sentido hacia dentro, pudiendo ser completamente neutralizadas por sendas fuerzas de reacción vincular normales al alambre y con sentido hacia fuera. Sin embargo, la bolita B no estaría en una posición de equilibrio en este supuesto porque su resultante de fuerzas activas tiene sentido hacia fuera, y el alambre no podría evitar que la bolita escapase hacia fuera perdiendo el contacto con él (dada su incapacidad para ejercer fuerza de reacción vincular hacia dentro). Por otra parte, dado que el alambre sigue siendo liso en el presente supuesto, la bolita C tampoco estaría en posición de equilibrio (tal como se ha razonado en la solución de la cuestión original).

Por último, se sugiere al alumnado que trate de responder a esta misma cuestión para un tercer supuesto: que las bolitas estuviesen apoyadas sobre la parte interna del alambre (vínculo unilateral).