No Boletín - Cuestión sobre curva de potencial II (Ex.Ene/13)

Enunciado

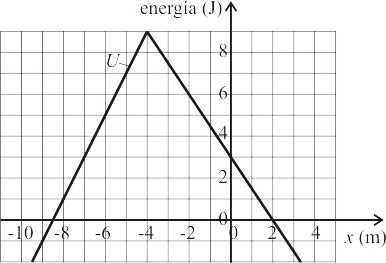
Una partícula de masa $1\,\mathrm {kg} \,$ se mueve a lo largo del eje $OX\,$ bajo la acción de una fuerza conservativa cuya energía potencial $U\,$ es la representada en la gráfica. Sabemos que en el instante $t=t_{0}\,$ la partícula se halla en la posición $x_{0}=-8\,\mathrm {m} \,$ y tiene una celeridad $v_{0}=2\,\mathrm {m/s} \,$ en el sentido positivo del eje $OX\,$.

¿Cuál de las siguientes afirmaciones sobre el movimiento de la partícula para $t>t_{0}\,$ es falsa? (NOTA: sólo una de las cuatro afirmaciones es falsa).

(a) Alcanzará un equilibrio inestable en la posición $x=-4\,\mathrm {m} \,$

(b) Nunca pasará por la posición $x=1\,\mathrm {m} \,$

(c) En algún momento entrará en la región $x<-8\,\mathrm {m} \,$

(d) Estará en reposo instantáneo en la posición $x=-7\,\mathrm {m} \,$

Energía mecánica

Es un movimiento rectilíneo conservativo. La energía mecánica $E\,$ (suma de la energía cinética y la energía potencial) es constante en el tiempo. La calculamos evaluándola en el instante inicial:

$E={\frac {1}{2}}mv_{0}^{2}+U(x_{0})=2\,\mathrm {J} +1\,\mathrm {J} =3\,\mathrm {J}$

donde $m\,$ es la masa de la partícula, $x_{0}\,$ es su posición inicial, y $v_{\,0}\,$ es su celeridad inicial (valores dados en el enunciado).

Nota: la evaluación de $U(x_{0})\,$ se realiza mediante la simple inspección de la gráfica facilitada.

Puntos de retorno y región prohibida

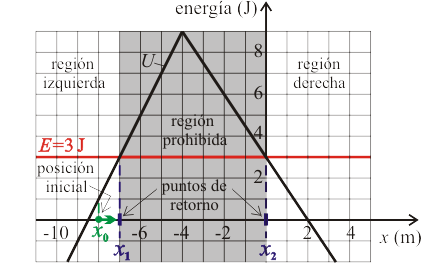
Los puntos de retorno corresponden a los valores de $x\,$ para los cuales se produce intersección entre la curva de energía potencial $U(x)\,$ y la recta horizontal representativa de la energía mecánica constante $E=3\,\mathrm {J} \,$. Observamos en la gráfica que existen dos puntos de retorno:

$x_{1}=-7\,\mathrm {m} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,x_{2}=0\,\mathrm {m}$

Se denominan "de retorno" porque, si la partícula llega a uno de estos puntos, sufrirá allí la anulación instantánea de su celeridad y la inversión del sentido de su movimiento. Esta inversión del sentido de movimiento se debe a que cada punto de retorno es la frontera entre una región permitida y una región prohibida.

En efecto, la energía cinética de una partícula es, por definición, mayor o igual que cero (no negativa) y, por tanto, la partícula tiene prohibido su acceso a aquella región del eje $OX\,$ para la cual la curva de energía potencial $U(x)\,$ está por encima de la recta horizontal de energía mecánica $E=3\,\mathrm {J} \,$. En el caso que nos ocupa:

$x_{1}<x<x_{2}\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\frac {1}{2}}m{\dot {x}}^{\,2}=K=E-U(x)<0\,\,\,\,\mathrm {(imposible)} \,\,\,\,\,\Longrightarrow \,\,\,\,\,\mathrm {region} \,\,\mathrm {prohibida}$

¿Cuál es la afirmación FALSA?

Dado que la partícula se halla inicialmente en $x_{0}=-8\,\mathrm {m}$ y moviéndose hacia la derecha (${\dot {x}}>0\,$), es obvio que la partícula alcanzará el punto de retorno $x_{1}=-7\,\mathrm {m} \,$. En dicho punto estará en reposo instantáneo y, a continuación, empezará a moverse hacia la izquierda (${\dot {x}}<0\,$) de forma permanente (porque, a la izquierda de $x_{1}\,$, no hay puntos de retorno).

Por tanto, es CORRECTA la afirmación (d): "Estará en reposo instantáneo en la posición $x=-7\,\mathrm {m} \,$", ya que dicha posición va a ser efectivamente alcanzada por la partícula y es un punto de retorno:

$\mathrm {para} \,\,\,x=x_{1}=-7\,\mathrm {m} \,\,\,\,\,\Longrightarrow \,\,\,\,\,{\frac {1}{2}}m{\dot {x}}^{\,2}=K=E-U(x_{1})=0\,\,\,\,\,\Longrightarrow \,\,\,\,\,{\dot {x}}=0\,\,\,\,\mathrm {(reposo} \,\,\mathrm {instantaneo)}$

Y también es CORRECTA la afirmación (c): "En algún momento entrará en la región $x<-8\,\mathrm {m} \,$", ya que, tras invertir su sentido de movimiento en $x=x_{1}\,$, la partícula se moverá indefinidamente hacia la izquierda (sin retorno), cumpliéndose que:

$\lim _{t\rightarrow \infty }x(t)=-\infty$

En la gráfica observamos que existen dos regiones permitidas para el movimiento de la partícula: la región izquierda ($x\leq x_{1}\,$) y la región derecha ($x\geq x_{2}\,$), pero estas dos regiones están inconexas entre sí debido a que entre ambas se interpone la región prohibida ($x_{1}<x<x_{2}\,$). Podemos expresarlo diciendo que existe una barrera de potencial que impide el paso de una región a otra. Por tanto, el movimiento de la partícula transcurrirá de facto sólo en una de las dos regiones permitidas. Pero... ¿en cuál? Pues muy fácil: en aquella región en la que se halle la partícula en el instante inicial. En nuestro caso, al ser $x_{0}=-8\,\mathrm {m} <x_{1}=-7\,\mathrm {m} \,$, la partícula se va a mover siempre en la región izquierda y nunca alcanzará la región derecha. Por tanto, es CORRECTA la afirmación (b): "Nunca pasará por la posición $x=1\,\mathrm {m} \,$", ya que esta posición pertenece a la región derecha:

$1\,\mathrm {m} >x_{2}=0\,\mathrm {m}$

Por eliminación, llegamos finalmente a la conclusión de que la afirmación falsa que buscábamos es la (a): "Alcanzará un equilibrio inestable en la posición $x=-4\,\mathrm {m} \,$". En efecto, sin necesidad de entrar a discutir otras características de la posición $x=-4\,\mathrm {m} \,$, la afirmación (a) es FALSA porque dicha posición queda dentro de la región prohibida:

$x_{1}=-7\,\mathrm {m} <-4\,\mathrm {m} <x_{2}=0\,\mathrm {m}$

y, por tanto, es inalcanzable para la partícula.