No Boletín - Muelle en plano inclinado (Ex.Nov/10)

Enunciado

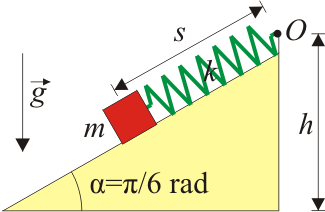
Una partícula de masa $m$ se halla inicialmente en reposo a una altura $h$ (punto $O$). La partícula comienza a deslizar sin rozamiento sobre un plano inclinado un ángulo $\alpha =\pi /6$ rad, bajo la acción de su propio peso y manteniéndose conectada con el punto $O$ mediante un resorte de constante $k$ y longitud natural nula.

1. ¿Qué distancia recorre la partícula hasta que se para por primera vez?
2. Cuando la partícula se encuentra a una distancia $s$ de $O$, ¿cuánto vale el módulo de la fuerza de reacción vincular?

Distancia máxima

La máxima distancia de la masa al punto de partida se calcula por aplicación de la ley de conservación de la energía mecánica.

Físicamente lo que ocurre es que al soltar la masa, la gravedad tira de ella hacia abajo, pero al descender por el plano, se va estirando el muelle y aumentando la fuerza recuperadora. Llega un momento en que la masa se para y a partir de ahí vuelve a subir hasta la posición inicial, repitiéndose el proceso.

La posición de máximo alejamiento NO la da la condición de que la fuerza elástica iguale a la componente del peso en la dirección de movimiento. Esa condición nos da la posición de equilibrio, en la que la aceleración es nula. Pero a nosotros no nos interesa dónde se anula aceleración, sino dónde se anula la velocidad, y para ello necesitamos la ley de conservación de la energía mecánica.

La partícula se encuentra sometida a tres fuerzas: su peso, la fuerza elástica y la reacción del plano. Puesto que el plano inclinado constituye un vínculo liso esclerónomo, la fuerza de reacción vincular es puramente normal al plano y no realiza trabajo sobre la partícula. Dado que las otras dos fuerzas son conservativas, se conserva la energía mecánica

$E=K+U=\mathrm {cte} \,$

Tanto la posición inicial como la de máxima distancia son de reposo instantáneo (pues la máxima distancia implica que la masa se para y a partir de ahí comienza a retroceder). Por tanto la energía cinética es nula en ambos casos.

Si la energía cinética es nula, toda la energía mecánica es potencial. Inicialmente, toda la energía es debida al peso, pero a medida que se estira el muelle se va almacenando energía potencial elástica. En el máximo alejamiento, parte de la energía potencial gravitatoria se ha convertido en elástica, cumpliéndose la relación

$mgz={\frac {1}{2}}ks^{2}$

donde hemos llamado $z$ a la altura descendida, la cual se relaciona con la distancia recorrida mediante la igualdad

$z=s\,\mathrm {sen} \left({\frac {\pi }{6}}\right)={\frac {s}{2}}$

Sustituyendo en la ley de conservación de la energía

$mg{\frac {s}{2}}={\frac {1}{2}}ks^{2}\,\,\,$  ⇒  $\,\,\,s={\frac {mg}{k}}$

Fuerza de reacción vincular

Si descomponemos la segunda ley de Newton en la parte tangencial y la normal al plano tenemos

$m{\vec {a}}=m{\vec {g}}-k{\vec {r}}+{\vec {\Phi }}$ ⇒ $\left\{{\begin{matrix}m{\vec {a}}_{t}&=&m{\vec {g}}_{\parallel }-k{\vec {r}}\\m{\vec {a}}_{n}&=&m{\vec {g}}_{\perp }+{\vec {\Phi }}\end{matrix}}\right.$

donde hemos tenido en cuenta que la fuerza debida al muelle es puramente tangencial al plano, mientras que la reacción es puramente normal.

La aceleración normal es nula, por tratarse de un movimiento rectilíneo, por lo que obtenemos

${\vec {\Phi }}=-m{\vec {g}}_{\perp }\,\,\,$  ⇒  $\,\,\,\Phi =\left|m{\vec {g}}_{\perp }\right|=mg\cos \left({\frac {\pi }{6}}\right)=mg{\frac {\sqrt {3}}{2}}$