Diferencia entre revisiones de «Problemas de electrostática en el vacío (GIOI)»
Secciones
| (No se muestran 48 ediciones intermedias del mismo usuario) | |||
| Línea 11: | Línea 11: | ||
==Fuerza entre cargas en un triángulo== | ==Fuerza entre cargas en un triángulo== | ||
Tres cargas puntuales iguales +''q'' se hallan en los vértices de un triángulo equilátero de lado ''b''. Calcule la fuerza eléctrica sobre cada una de ellas. | Tres cargas puntuales iguales +''q'' se hallan en los vértices de un triángulo equilátero de lado ''b''. | ||
# Calcule la fuerza eléctrica sobre cada una de ellas. | |||
# Suponga que se cambia una de las cargas +''q'' por una carga −''q''. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas? | |||
# Si se cambia una segunda carga +''q'' por otra carga –''q'', ¿cuánto pasa a ser la fuerza sobre cada una? | |||
# Por último, si se sustituye la última carga +''q'' por otra –''q'', ¿cuál es ahora la fuerza? | |||
Suponga que se | [[Fuerza entre cargas en un triángulo|Solución]] | ||
==Cuatro cargas en dos varillas== | |||
{{Nivel|3}} Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +''q'', unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±''q''. Las cuatro cargas forman un cuadrado de lado ''b''. | |||
Para cada varilla, calcule la fuerza resultante y el momento resultante respecto a su centro de masas (centro de cada varilla). | |||
[[Archivo:4cargas-dos-varillas.png|centro]] | |||
[[Cuatro cargas en dos varillas|Solución]] | |||
==Fuerzas y momentos sobre un par de cargas== | |||
{{nivel|2}} Dos cargas <math>q_1=+q</math> y <math>q_2=-q</math> se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico | |||
<center><math>\vec{E}=Ay\vec{\imath}+Bx^2 \vec{\jmath}</math></center> | |||
* Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\imath}</math> y <math>\vec{r}_2=-b\vec{\imath}</math>, ¿cuál es el efecto del campo sobre el sistema? | |||
* Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\jmath}</math> y <math>\vec{r}_2=-b\vec{\jmath}</math>, ¿cuál es el efecto del campo sobre el sistema? | |||
[[Fuerzas y momentos sobre un par de cargas|Solución]] | |||
==Campo de dos cargas puntuales== | |||
{{nivel|2}}Se tienen dos cargas <math>q_1</math> y <math>q_2</math> situadas respectivamente en los puntos <math>\vec{r}_1=-12\vec{\imath}</math> (cm) y <math>\vec{r}_2=+12\vec{\imath}</math> (cm). Halle el campo eléctrico en los puntos | |||
<math>\vec{r}_A=\vec{0}</math>, <math>\vec{r}_B=28\vec{\imath}</math>, <math>\vec{r}_C=9\vec{\jmath}</math>, <math>\vec{r}_D=-9\vec{k}</math>, <math>\vec{r}_E=12\vec{\imath}+32\vec{\jmath}</math> | |||
(todas las distancias en cm) para los cuatro casos siguientes | |||
# <math>q_1=q_2=+1\,\mathrm{nC}</math> | |||
# <math>q_1=+1\,\mathrm{nC}</math>, <math>q_2=-1\,\mathrm{nC}</math> | |||
# <math>q_1=+1\,\mathrm{nC},q_2=+9\,\mathrm{nC}</math> | |||
# <math>q_1=+1\,\mathrm{nC},q_2=-9\,\mathrm{nC}</math> | |||
[[Campo de dos cargas puntuales (GIOI)|Solución]] | |||
==Anulación de campo eléctrico== | |||
{{nivel|2}} Para los cuatro pares de cargas del [[Campo de dos cargas puntuales (GIOI)|problema anterior]], localice el punto del eje OX en que se anula el campo eléctrico. | |||
[[Anulación de campo eléctrico (GIOI)|Solución]] | |||
==Cargas en los vértices de un cuadrado== | |||
Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide 20 cm, según ilustra la figura. Los valores de todas las cargas son +10 nC o −10 nC | |||
# {{nivel|1}} ¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado? | |||
# {{nivel|1}} ¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito? | |||
# {{nivel|2}} Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema? | |||
# {{nivel|3}} ¿Qué trabajo hay que realizar para permutar una carga positiva por una negativa vecina? | |||
<center>[[Archivo:Cuatro-cargas-cuadrado.png]]</center> | |||
[[Cargas en los vértices de un cuadrado (GIOI)|Solución]] | |||
==Campo de un anillo homogéneo== | |||
{{nivel|3}} Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio ''b'' que almacena una carga ''Q'' distribuida uniformemente. | |||
[[Campo de un anillo homogéneo (GIOI)|Solución]] | |||
==Campo de un disco homogéneo== | |||
{{nivel|3}} A partir del resultado del problema “[[Campo de un anillo homogéneo (GIOI)|Campo de un anillo homogéneo]]” calcule el campo en los puntos del eje de un disco circular de radio ''b'', en el cual existe una carga ''Q'' distribuida uniformemente. | |||
[[Campo de un disco homogéneo (GIOI)|Solución]] | |||
==Campo de un plano infinito== | |||
{{nivel|1}} Empleando el resultado del problema “[[Campo de un disco homogéneo (GIOI)|Campo de un disco homogéneo]]”, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga <math>\sigma_0</math>. | |||
[[Campo de un plano infinito (GIOI)|Solución]] | |||
==Campo de dos planos paralelos== | |||
{{nivel|1}} Suponga que se tienen dos planos infinitos paralelos separados una distancia ''b'' que almacenan respectivamente densidades de carga <math>+\sigma_0</math> y <math>-\sigma_0</math>. Calcule el campo eléctrico en todos los puntos del espacio. | |||
[[Campo de dos planos paralelos (GIOI)|Solución]] | |||
==Campo de dos discos paralelos== | |||
Se tienen dos discos de radio 1cm y con cargas respectivas de ±12 nC situados paralelamente al plano OXY, con sus centros en <math>(\pm b/2) \vec{k}</math>. Halle el valor aproximado del campo eléctrico en el origen de coordenadas si: | |||
# {{nivel|1}} <math>b=1\mathrm{m}</math>. | |||
# {{nivel|1}} <math>b=1\,\mathrm{mm}</math>. | |||
# {{nivel|3}} <math>b</math> tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores. | |||
[[Campo de dos discos paralelos (GIOI)|Solución]] | |||
==Campo eléctrico de un anillo no homogéneo== | |||
{{nivel|4}} Un anillo de radio R se encuentra cargado con una densidad lineal de carga <math>\lambda =\lambda_0\cos^2(\theta'/2)</math>. El anillo se encuentra situado en el plano OXY, centrado en el origen. θ' es la coordenada angular en cilíndricas (ángulo que el vector de posición forma con OX). | |||
# ¿Cuánto vale la carga total del anillo? | |||
# ¿Cuánto vale el campo eléctrico en el centro del anillo? | |||
# ¿Y el potencial eléctrico en el mismo punto? | |||
[[Campo eléctrico de un anillo no homogéneo|Solución]] | |||
==Campo de un segmento== | |||
{{nivel|4}} Calcule el campo eléctrico producido por un segmento rectilíneo de longitud <math>2a</math> cargado uniformemente con una densidad de carga <math>\lambda_0</math>, en cualquier punto del plano perpendicular al segmento por su punto medio. | |||
[[Campo de un segmento (GIOI)|Solución]] | |||
==Campo de un hilo infinito== | |||
{{nivel|2}} A partir del resultado del problema “[[Campo de un segmento (GIOI)|Campo de un segmento]]”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea <math>\lambda_0</math>. | |||
Este campo puede también hallarse mediante la ley de Gauss. ¿Cómo se llega en ese caso al resultado? | |||
[[Campo de un hilo infinito (GIOI)|Solución]] | |||
==Campo de dos hilos paralelos== | |||
Una línea de alta tensión puede modelarse como dos hilos paralelos, infinitamente largos, cargados con densidades <math>\pm\lambda_0</math>. Si situamos los ejes de forma que los hilos son paralelos al eje OZ y pasan por los puntos <math>\pm b\vec{\imath}</math>, | |||
# Halle la fuerza que cada hilo produce sobre un segmento de longitud ''ℓ'' del otro. | |||
# Calcule el campo eléctrico en todos los puntos del espacio. | |||
[[Campo de dos hilos paralelos (GIOI)|Solución]] | |||
==Flujo del campo eléctrico de un cubo== | |||
{{nivel|2}} Un cubo de arista b contiene una carga <math>Q_0</math> distribuida uniformemente en su volumen. No hay más cargas en el sistema. Sea ''S'' una superficie esférica de radio ''b'' centrada en uno de los vértices del cubo. ¿Cuánto vale el flujo del campo eléctrico a través de ''S''? | |||
[[Archivo:cubo-interseccion-esfera.png|center]] | |||
[[Flujo del campo eléctrico de un cubo (GIOI)|Solución]] | |||
==Campo de distribuciones esféricas== | |||
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica: | |||
# {{nivel|2}} Una superficie esférica de radio a que almacena una carga ''Q'' distribuida uniformemente. | |||
# {{nivel|2}} Dos superficies esféricas concéntricas, de radios ''a'' y ''b'' (''a'' < ''b'') que almacenan respectivamente cargas +Q y -Q, distribuidas uniformemente. | |||
# {{nivel|2}} Dos superficies esféricas concéntricas, de radios ''a'' y ''b'' (''a'' < ''b'') cargadas respectivamente con densidades superficiales uniformes <math>+\sigma_0</math> y <math>-\sigma_0</math>. | |||
# {{nivel|3}} Una esfera maciza de radio ''b'' que almacena una carga Q distribuida uniformemente en su volumen. | |||
# {{nivel|4}} Una esfera maciza de radio <math>2b</math> con una densidad de carga dependiente de la distancia al centro como <math>\rho(r) = A(b-r)</math> (<math>r < 2b</math>). | |||
[[Campo de distribuciones esféricas (GIOI)|Solución]] | |||
==Dos superficies esféricas cargadas== | |||
Se tiene un sistema formado por dos superficies esféricas cargadas (“1” y “2”), de radios 4''b'' y 2''b'', respectivamente. La superficie “2” se encuentra parcialmente en el interior de la “1”, centrada a una distancia 3b del centro de la “1”, punto que tomamos como origen de coordenadas. La superficie “1” almacena una carga +''Q'' y la “2” una carga −''Q'', ambas distribuidas uniformemente sobre cada superficie | |||
[[Archivo:dos-superficies-esfericas-01.png|500px|center]] | |||
# Calcule el campo eléctrico en los siguientes puntos del plano OXY: | |||
## El origen de coordenadas <math>O(0,0)</math> | |||
## El centro de la esfera “2” <math>A(3b,0)</math> | |||
## El punto <math>B_1(b^-,0)</math> situado justo fuera de la esfera “2” y el punto <math>B_2(b^+,0)</math> situado justo dentro de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto? | |||
## El punto <math>C_1(4b^-,0)</math> situado justo dentro de la esfera “1” y el punto <math>C_2(4b^+,0)</math> situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto? | |||
## El punto <math>D_1(0,4b^-)</math> situado justo dentro de la esfera “1” y el punto <math>D_2(0,4b^+)</math> situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto? | |||
# Calcule el potencial eléctrico en los puntos anteriores, tomando como origen de potencial el infinito. | |||
# Halle el trabajo necesario para llevar una carga puntual q_0 desde el punto <math>G(6b,0)</math> al punto <math>H(-6b,0)</math> siguiendo un camino rectilíneo. | |||
# En puntos alejados del sistema, éste se ve como un dipolo eléctrico. ¿Cuál es el momento dipolar de la distribución? | |||
[[Dos superficies esféricas cargadas|Solución]] | |||
==Esfera con hueco esférico== | |||
Se tiene una carga <math>Q=14\,\mathrm{nC}</math> distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 m de la esfera grande. | |||
[[Archivo:esfera-hueco-01.png|400px|center]] | |||
Calcule el campo eléctrico producido por este sistema en los siguientes puntos: | |||
# ''O'', el centro de la esfera grande. | |||
# ''C'', el centro del hueco. | |||
# ''A'', el borde exterior del hueco. | |||
# ''B'', el punto diametralmente opuesto a A. | |||
# ''P'', un punto situado a 25 cm del origen O en la dirección de X positivo. | |||
[[Esfera con hueco esférico|Solución]] | |||
==Potencial de cargas puntuales== | |||
Halle el potencial eléctrico en los puntos indicados en el problema “[[Campo de dos cargas puntuales (GIOI)|Campo de dos cargas puntuales]]”, para los pares de cargas descritos en el mismo problema. | |||
[[Potencial de dos cargas puntuales (GIOI)|Solución]] | |||
==Trabajo para cargas en un triángulo== | |||
Calcule el trabajo necesario para realizar cada una de las sustituciones descritas en el problema “[[Fuerza entre cargas en un triángulo]]”. | |||
[[Trabajo para cargas en un triángulo (GIOI)|Solución]] | |||
==Potencial debido a una superficie esférica== | |||
Halle el potencial en todos los puntos del espacio creado por una carga ''Q'' distribuida uniformemente sobre una superficie esférica de radio ''b''. | |||
[[Potencial debido a una superficie esférica (GIOI)|Solución]] | |||
==Diferencia de potencial entre dos planos paralelos== | |||
Para el sistema del problema “[[Campo de dos planos paralelos (GIOI)|Campo de dos planos paralelos]]”, calcule la diferencia de potencial entre el plano cargado positivamente y el cargado negativamente. | |||
[[Diferencia de potencial entre dos planos paralelo|Solución]] | |||
==Potencial de distribuciones esféricas== | |||
Calcule el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema “[[Campo_de_distribuciones_esféricas_(GIOI)|Campo de distribuciones esféricas]]”. | |||
[[Potencial de distribuciones esféricas|Solución]] | |||
==Potencial debido a un anillo cargado== | |||
Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia ''z'' al plano del anillo. | |||
¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo? | |||
Supongamos que en lugar de una carga positiva tenemos una de -2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia <math>z=1.0\,\mathrm{mm}</math> del centro del anillo, ¿qué tipo de movimiento describe esta carga? | |||
[[Potencial_eléctrico_en_el_eje_de_un_anillo|Solución]] | |||
==Potencial de esfera con hueco== | |||
Para la esfera horadada del problema “[[Esfera con hueco esférico]]”, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros. | |||
[[Potencial de esfera con hueco (GIOI)|Solución]] | |||
==Energía de un tetraedro de cargas== | |||
En los cuatro vértices de un tetraedro regular de arista ''b'' tenemos sendas cargas que pueden valer cada una +''q'' o –''q''. ¿Qué valores puede tener la energía electrostática de este sistema? Si la probabilidad de que una carga de un vértice sea positiva o negativa es del 50%, ¿cuál es el valor esperado de la energía? | |||
[[Energía de un tetraedro de cargas|Solución]] | |||
==Energía de un sistema de cuatro cargas== | |||
Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales: | |||
# <math>q_1=q_2=q_3=q_4=+14\,\mathrm{nC}</math>. | |||
# <math>q_1=q_2=q_3=q_4=-14\,\mathrm{nC}</math>. | |||
# <math>q_1=q_3=+14\,\mathrm{nC}</math>, <math>q_2=q_4=-14\,\mathrm{nC}</math>. | |||
# <math>q_1=q_2=+14\,\mathrm{nC}</math>, <math>q_3=q_4=-14\,\mathrm{nC}</math>. | |||
# <math>q_1=q_4=+14\,\mathrm{nC}</math>, <math>q_2=q_3=-14\,\mathrm{nC}</math>. | |||
situadas en cada caso en los vértices de un rectángulo <math>\vec{r}_1 = \vec{0}</math>, <math>\vec{r}_2 = 7\vec{\imath}</math> cm, <math>\vec{r}_3 = (7\vec{\imath}+24\vec{\jmath} )</math> cm, <math>\vec{r}_2 =24\vec{\jmath}</math> cm | |||
[[Energía de un sistema de cuatro cargas (GIOI)|Solución]] | |||
[[ | ==Energía de superficies esféricas== | ||
Calcule la energía electrostática almacenada en las siguientes distribuciones de carga: | |||
# Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga Q. | |||
# Dos superficies esféricas concéntricas de radios ''a'' y ''b'' (''a'' < ''b'') sobre las cuales hay distribuidas uniformemente cargas +Q y -Q respectivamente. | |||
# Dos superficies esféricas concéntricas de radios ''a'' y ''b'' (''a'' < ''b'') sobre las cuales hay distribuidas cargas con densidades <math>+\sigma_0</math> y <math>-\sigma_0</math> respectivamente. | |||
# Tres superficies esféricas concéntricas de radios <math>2b</math>, <math>3b</math> y <math>6b</math>, que almacenan, respectivamente, cargas <math>Q_1</math>, <math>Q_2</math> y <math>Q_3</math>. ¿A qué se reduce el resultado si <math>Q_1=Q_3=Q_0</math>, <math>Q_2=-Q_0</math>? | |||
[[Energía de superficies esféricas (GIOI)|Solución]] | |||
==Campo eléctrico radial== | |||
En una región del espacio el campo eléctrico es radial desde el origen de coordenadas <math>\vec{E}=E(r) \vec{u}_r</math>, dependiendo de la distancia al centro según la gráfica adjunta. El valor máximo del campo es <math>E_0</math>. | |||
# ¿Cuánto valen las densidades de carga que producen este campo? | |||
# ¿Cuánto vale el potencial eléctrico en el origen de coordenadas (tomando como origen de potencial el infinito)? | |||
# ¿Cuánta energía almacena este sistema? | |||
[[Archivo:campo-radial-01.png|500px|center]] | |||
[[Campo eléctrico radial (GIOI)|Solución]] | |||
==Campo eléctrico central== | |||
El campo eléctrico en todos los puntos del espacio viene dado por la expresión | |||
<center><math>\vec{E}=\left\{\begin{array}{rcc}E_0 \left(\dfrac{r}{b}\right)^2 \vec{u}_r& &(r<b)\\ && \\ E_0 \left(\dfrac{b}{r}\right)^2 \vec{u}_r& &(r>b)\end{array}\right.</math></center> | |||
# ¿Cuánto vale la carga total almacenada en el sistema? | |||
# ¿Cuánto vale la densidad de carga ρ = ρ(r)? | |||
# ¿Cuánto vale el potencial eléctrico en el origen de coordenadas (tomando como origen de potencial el infinito)? | |||
# ¿Cuánta energía almacena este sistema? | |||
[[Campo eléctrico central (GIOI)|Solución]] | |||
==Campo y potencial de dos planos ortogonales== | |||
Un sistema de cargas está formado por dos planos cargados, ambos con la misma densidad de carga <math>+\sigma_0</math>, situados ortogonalmente. Uno de ellos coincide con el plano OXZ y el otro con el OYZ. | |||
# Halle el campo eléctrico en los puntos <math>A(4b,3b,0)</math>, <math>B(-4b,3b,0)</math>, <math>C(-3b,-4b,0)</math> y <math>D(2b,-5b,0)</math>. Puede usarse, si se conoce, la expresión del campo creado por un solo plano. | |||
# Indique gráficamente cómo son las líneas de campo en cada uno de los cuatro cuadrantes. | |||
# Indique gráficamente cómo son las superficies equipotenciales en este sistema | |||
# Calcule el trabajo necesario para mover una carga q_0 desde A hasta B; para mover la misma carga desde A a C, y para moverla desde A a D. | |||
# Suponga que se sitúa una carga <math>-q_0</math> en el punto A y otra <math>+q_0</math> en la posición simétrica B ¿Cuánto vale la fuerza eléctrica sobre cada una de estas dos cargas? | |||
[[Archivo:campo-planos-ortogonales.png|520px|center]] | |||
[[Campo y potencial de dos planos ortogonales (GIOI)|Solución]] | |||
==Campo de tres cargas alineadas== | |||
Se tienen dos cargas puntuales, de valores <math>q_1=1\,\mathrm{nC}</math> y <math>q_2=4\,\mathrm{nC}</math> situadas respectivamente en los puntos A(0,0,0) y B(1,0,0) (m). ¿En qué punto hay que situar y qué valor debe tener una nueva carga si se desea que la fuerza sobre cada una de las tres cargas sea nula? | |||
[[Campo de tres cargas alineadas|Solución]] | |||
Revisión actual - 21:42 15 abr 2025
Carga total de una distribución
Calcule la carga total de las siguientes distribuciones de carga:
 N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en .
N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en . Un anillo circular de radio b con una densidad lineal de carga uniforme .
Un anillo circular de radio b con una densidad lineal de carga uniforme . Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX.
Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX. Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga .
Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga . Una esfera maciza de radio b con densidad de carga uniforme .
Una esfera maciza de radio b con densidad de carga uniforme . Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Fuerza entre cargas en un triángulo
Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado b.
- Calcule la fuerza eléctrica sobre cada una de ellas.
- Suponga que se cambia una de las cargas +q por una carga −q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas?
- Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una?
- Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza?
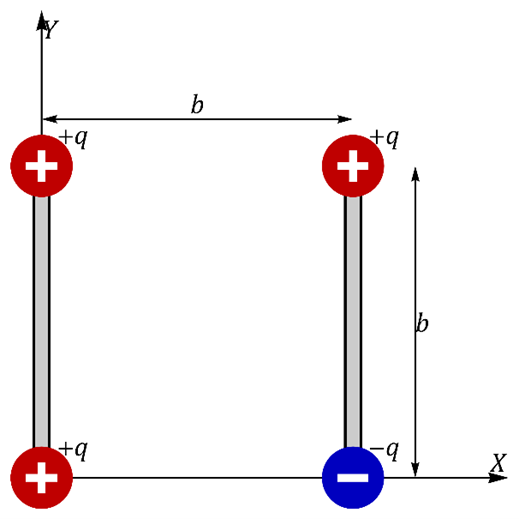
Cuatro cargas en dos varillas
![]() Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +q, unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±q. Las cuatro cargas forman un cuadrado de lado b.
Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +q, unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±q. Las cuatro cargas forman un cuadrado de lado b.
Para cada varilla, calcule la fuerza resultante y el momento resultante respecto a su centro de masas (centro de cada varilla).
Fuerzas y momentos sobre un par de cargas
![]() Dos cargas y se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico
Dos cargas y se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico
- Si los extremos de la varilla se encuentran en y , ¿cuál es el efecto del campo sobre el sistema?
- Si los extremos de la varilla se encuentran en y , ¿cuál es el efecto del campo sobre el sistema?
Campo de dos cargas puntuales
![]() Se tienen dos cargas y situadas respectivamente en los puntos (cm) y (cm). Halle el campo eléctrico en los puntos
, , , ,
Se tienen dos cargas y situadas respectivamente en los puntos (cm) y (cm). Halle el campo eléctrico en los puntos
, , , ,
(todas las distancias en cm) para los cuatro casos siguientes
- ,
Anulación de campo eléctrico
![]() Para los cuatro pares de cargas del problema anterior, localice el punto del eje OX en que se anula el campo eléctrico.
Para los cuatro pares de cargas del problema anterior, localice el punto del eje OX en que se anula el campo eléctrico.
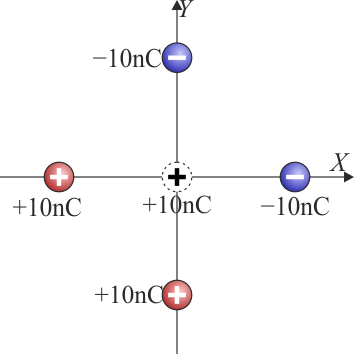
Cargas en los vértices de un cuadrado
Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide 20 cm, según ilustra la figura. Los valores de todas las cargas son +10 nC o −10 nC
 ¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado?
¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado? ¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito?
¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito? Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema?
Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema? ¿Qué trabajo hay que realizar para permutar una carga positiva por una negativa vecina?
¿Qué trabajo hay que realizar para permutar una carga positiva por una negativa vecina?
Campo de un anillo homogéneo
![]() Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio b que almacena una carga Q distribuida uniformemente.
Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio b que almacena una carga Q distribuida uniformemente.
Campo de un disco homogéneo
![]() A partir del resultado del problema “Campo de un anillo homogéneo” calcule el campo en los puntos del eje de un disco circular de radio b, en el cual existe una carga Q distribuida uniformemente.
A partir del resultado del problema “Campo de un anillo homogéneo” calcule el campo en los puntos del eje de un disco circular de radio b, en el cual existe una carga Q distribuida uniformemente.
Campo de un plano infinito
![]() Empleando el resultado del problema “Campo de un disco homogéneo”, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga .
Empleando el resultado del problema “Campo de un disco homogéneo”, halle el campo eléctrico en cualquier punto del espacio debido a un plano infinito cargado uniformemente con una densidad de carga .
Campo de dos planos paralelos
![]() Suponga que se tienen dos planos infinitos paralelos separados una distancia b que almacenan respectivamente densidades de carga y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\sigma_0}
. Calcule el campo eléctrico en todos los puntos del espacio.
Suponga que se tienen dos planos infinitos paralelos separados una distancia b que almacenan respectivamente densidades de carga y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\sigma_0}
. Calcule el campo eléctrico en todos los puntos del espacio.
Campo de dos discos paralelos
Se tienen dos discos de radio 1cm y con cargas respectivas de ±12 nC situados paralelamente al plano OXY, con sus centros en . Halle el valor aproximado del campo eléctrico en el origen de coordenadas si:
 .
. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle b=1\,\mathrm{mm}}
.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle b=1\,\mathrm{mm}}
. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle b}
tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle b}
tiene un valor arbitrario. Estime el error cometido en los dos apartados anteriores.
Campo eléctrico de un anillo no homogéneo
![]() Un anillo de radio R se encuentra cargado con una densidad lineal de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda =\lambda_0\cos^2(\theta'/2)}
. El anillo se encuentra situado en el plano OXY, centrado en el origen. θ' es la coordenada angular en cilíndricas (ángulo que el vector de posición forma con OX).
Un anillo de radio R se encuentra cargado con una densidad lineal de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda =\lambda_0\cos^2(\theta'/2)}
. El anillo se encuentra situado en el plano OXY, centrado en el origen. θ' es la coordenada angular en cilíndricas (ángulo que el vector de posición forma con OX).
- ¿Cuánto vale la carga total del anillo?
- ¿Cuánto vale el campo eléctrico en el centro del anillo?
- ¿Y el potencial eléctrico en el mismo punto?
Campo de un segmento
![]() Calcule el campo eléctrico producido por un segmento rectilíneo de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2a}
cargado uniformemente con una densidad de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda_0}
, en cualquier punto del plano perpendicular al segmento por su punto medio.
Calcule el campo eléctrico producido por un segmento rectilíneo de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2a}
cargado uniformemente con una densidad de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda_0}
, en cualquier punto del plano perpendicular al segmento por su punto medio.
Campo de un hilo infinito
![]() A partir del resultado del problema “Campo de un segmento”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea .
A partir del resultado del problema “Campo de un segmento”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea .
Este campo puede también hallarse mediante la ley de Gauss. ¿Cómo se llega en ese caso al resultado?
Campo de dos hilos paralelos
Una línea de alta tensión puede modelarse como dos hilos paralelos, infinitamente largos, cargados con densidades Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \pm\lambda_0} . Si situamos los ejes de forma que los hilos son paralelos al eje OZ y pasan por los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \pm b\vec{\imath}} ,
- Halle la fuerza que cada hilo produce sobre un segmento de longitud ℓ del otro.
- Calcule el campo eléctrico en todos los puntos del espacio.
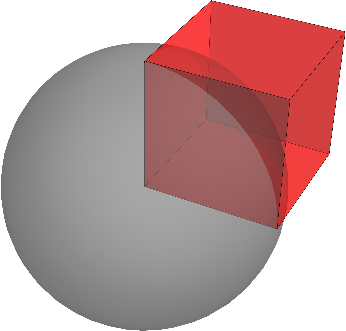
Flujo del campo eléctrico de un cubo
![]() Un cubo de arista b contiene una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_0}
distribuida uniformemente en su volumen. No hay más cargas en el sistema. Sea S una superficie esférica de radio b centrada en uno de los vértices del cubo. ¿Cuánto vale el flujo del campo eléctrico a través de S?
Un cubo de arista b contiene una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_0}
distribuida uniformemente en su volumen. No hay más cargas en el sistema. Sea S una superficie esférica de radio b centrada en uno de los vértices del cubo. ¿Cuánto vale el flujo del campo eléctrico a través de S?
Campo de distribuciones esféricas
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica:
 Una superficie esférica de radio a que almacena una carga Q distribuida uniformemente.
Una superficie esférica de radio a que almacena una carga Q distribuida uniformemente. Dos superficies esféricas concéntricas, de radios a y b (a < b) que almacenan respectivamente cargas +Q y -Q, distribuidas uniformemente.
Dos superficies esféricas concéntricas, de radios a y b (a < b) que almacenan respectivamente cargas +Q y -Q, distribuidas uniformemente. Dos superficies esféricas concéntricas, de radios a y b (a < b) cargadas respectivamente con densidades superficiales uniformes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle +\sigma_0}
y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\sigma_0}
.
Dos superficies esféricas concéntricas, de radios a y b (a < b) cargadas respectivamente con densidades superficiales uniformes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle +\sigma_0}
y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\sigma_0}
. Una esfera maciza de radio b que almacena una carga Q distribuida uniformemente en su volumen.
Una esfera maciza de radio b que almacena una carga Q distribuida uniformemente en su volumen. Una esfera maciza de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2b}
con una densidad de carga dependiente de la distancia al centro como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho(r) = A(b-r)}
(Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r < 2b}
).
Una esfera maciza de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2b}
con una densidad de carga dependiente de la distancia al centro como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho(r) = A(b-r)}
(Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r < 2b}
).
Dos superficies esféricas cargadas
Se tiene un sistema formado por dos superficies esféricas cargadas (“1” y “2”), de radios 4b y 2b, respectivamente. La superficie “2” se encuentra parcialmente en el interior de la “1”, centrada a una distancia 3b del centro de la “1”, punto que tomamos como origen de coordenadas. La superficie “1” almacena una carga +Q y la “2” una carga −Q, ambas distribuidas uniformemente sobre cada superficie
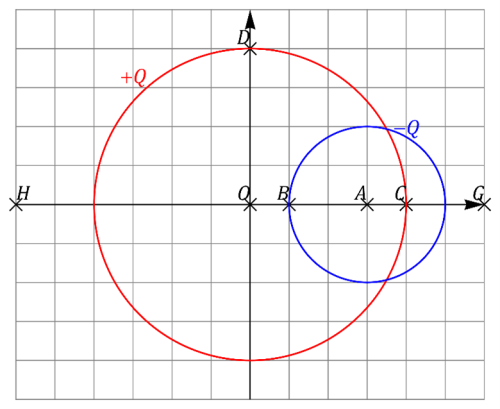
- Calcule el campo eléctrico en los siguientes puntos del plano OXY:
- El origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O(0,0)}
- El centro de la esfera “2” Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A(3b,0)}
- El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B_1(b^-,0)} situado justo fuera de la esfera “2” y el punto situado justo dentro de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
- El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_1(4b^-,0)} situado justo dentro de la esfera “1” y el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C_2(4b^+,0)} situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
- El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle D_1(0,4b^-)} situado justo dentro de la esfera “1” y el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle D_2(0,4b^+)} situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
- Calcule el potencial eléctrico en los puntos anteriores, tomando como origen de potencial el infinito.
- Halle el trabajo necesario para llevar una carga puntual q_0 desde el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G(6b,0)} al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle H(-6b,0)} siguiendo un camino rectilíneo.
- En puntos alejados del sistema, éste se ve como un dipolo eléctrico. ¿Cuál es el momento dipolar de la distribución?
Esfera con hueco esférico
Se tiene una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q=14\,\mathrm{nC}} distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 m de la esfera grande.
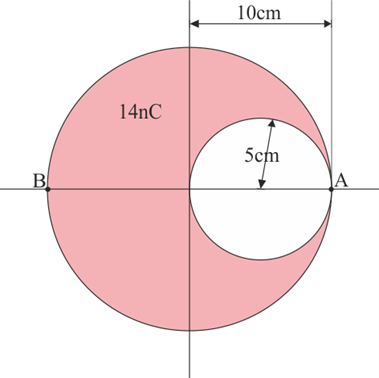
Calcule el campo eléctrico producido por este sistema en los siguientes puntos:
- O, el centro de la esfera grande.
- C, el centro del hueco.
- A, el borde exterior del hueco.
- B, el punto diametralmente opuesto a A.
- P, un punto situado a 25 cm del origen O en la dirección de X positivo.
Potencial de cargas puntuales
Halle el potencial eléctrico en los puntos indicados en el problema “Campo de dos cargas puntuales”, para los pares de cargas descritos en el mismo problema.
Trabajo para cargas en un triángulo
Calcule el trabajo necesario para realizar cada una de las sustituciones descritas en el problema “Fuerza entre cargas en un triángulo”.
Potencial debido a una superficie esférica
Halle el potencial en todos los puntos del espacio creado por una carga Q distribuida uniformemente sobre una superficie esférica de radio b.
Diferencia de potencial entre dos planos paralelos
Para el sistema del problema “Campo de dos planos paralelos”, calcule la diferencia de potencial entre el plano cargado positivamente y el cargado negativamente.
Potencial de distribuciones esféricas
Calcule el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema “Campo de distribuciones esféricas”.
Potencial debido a un anillo cargado
Halle el potencial eléctrico en todos los puntos del eje de un anillo de radio 1.00 cm sobre el cual hay distribuida una carga de 10.0 nC, como función de la distancia z al plano del anillo.
¿Qué trabajo es necesario realizar para llevar una carga de 2 nC desde el infinito hasta el centro de este anillo?
Supongamos que en lugar de una carga positiva tenemos una de -2 nC que solo puede moverse a lo largo del eje del anillo y que se suelta en reposo a una distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle z=1.0\,\mathrm{mm}} del centro del anillo, ¿qué tipo de movimiento describe esta carga?
Potencial de esfera con hueco
Para la esfera horadada del problema “Esfera con hueco esférico”, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.
Energía de un tetraedro de cargas
En los cuatro vértices de un tetraedro regular de arista b tenemos sendas cargas que pueden valer cada una +q o –q. ¿Qué valores puede tener la energía electrostática de este sistema? Si la probabilidad de que una carga de un vértice sea positiva o negativa es del 50%, ¿cuál es el valor esperado de la energía?
Energía de un sistema de cuatro cargas
Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=q_2=q_3=q_4=+14\,\mathrm{nC}} .
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=q_2=q_3=q_4=-14\,\mathrm{nC}} .
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=q_3=+14\,\mathrm{nC}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_2=q_4=-14\,\mathrm{nC}} .
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=q_2=+14\,\mathrm{nC}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_3=q_4=-14\,\mathrm{nC}} .
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=q_4=+14\,\mathrm{nC}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_2=q_3=-14\,\mathrm{nC}} .
situadas en cada caso en los vértices de un rectángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_1 = \vec{0}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_2 = 7\vec{\imath}} cm, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_3 = (7\vec{\imath}+24\vec{\jmath} )} cm, cm
Energía de superficies esféricas
Calcule la energía electrostática almacenada en las siguientes distribuciones de carga:
- Una superficie esférica de radio a sobre la cual hay distribuida uniformemente una carga Q.
- Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas uniformemente cargas +Q y -Q respectivamente.
- Dos superficies esféricas concéntricas de radios a y b (a < b) sobre las cuales hay distribuidas cargas con densidades y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\sigma_0} respectivamente.
- Tres superficies esféricas concéntricas de radios Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2b} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 3b} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 6b} , que almacenan, respectivamente, cargas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_1} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_3} . ¿A qué se reduce el resultado si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_1=Q_3=Q_0} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_2=-Q_0} ?
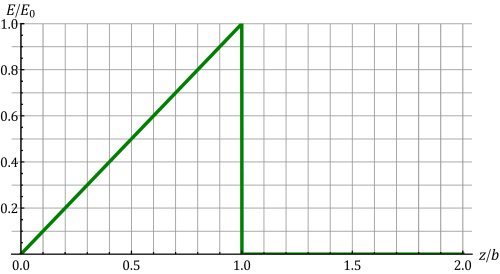
Campo eléctrico radial
En una región del espacio el campo eléctrico es radial desde el origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}=E(r) \vec{u}_r} , dependiendo de la distancia al centro según la gráfica adjunta. El valor máximo del campo es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle E_0} .
- ¿Cuánto valen las densidades de carga que producen este campo?
- ¿Cuánto vale el potencial eléctrico en el origen de coordenadas (tomando como origen de potencial el infinito)?
- ¿Cuánta energía almacena este sistema?
Campo eléctrico central
El campo eléctrico en todos los puntos del espacio viene dado por la expresión
- ¿Cuánto vale la carga total almacenada en el sistema?
- ¿Cuánto vale la densidad de carga ρ = ρ(r)?
- ¿Cuánto vale el potencial eléctrico en el origen de coordenadas (tomando como origen de potencial el infinito)?
- ¿Cuánta energía almacena este sistema?
Campo y potencial de dos planos ortogonales
Un sistema de cargas está formado por dos planos cargados, ambos con la misma densidad de carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle +\sigma_0} , situados ortogonalmente. Uno de ellos coincide con el plano OXZ y el otro con el OYZ.
- Halle el campo eléctrico en los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A(4b,3b,0)} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B(-4b,3b,0)} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C(-3b,-4b,0)} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle D(2b,-5b,0)} . Puede usarse, si se conoce, la expresión del campo creado por un solo plano.
- Indique gráficamente cómo son las líneas de campo en cada uno de los cuatro cuadrantes.
- Indique gráficamente cómo son las superficies equipotenciales en este sistema
- Calcule el trabajo necesario para mover una carga q_0 desde A hasta B; para mover la misma carga desde A a C, y para moverla desde A a D.
- Suponga que se sitúa una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -q_0} en el punto A y otra Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle +q_0} en la posición simétrica B ¿Cuánto vale la fuerza eléctrica sobre cada una de estas dos cargas?

Campo de tres cargas alineadas
Se tienen dos cargas puntuales, de valores Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_1=1\,\mathrm{nC}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle q_2=4\,\mathrm{nC}} situadas respectivamente en los puntos A(0,0,0) y B(1,0,0) (m). ¿En qué punto hay que situar y qué valor debe tener una nueva carga si se desea que la fuerza sobre cada una de las tres cargas sea nula?


































