Anulación de campo eléctrico (GIOI)

Enunciado

Para los cuatro pares de cargas del problema “Campo de dos cargas puntuales”, localice el punto del eje OX en que se anula el campo eléctrico.

Solución

Cargas del mismo signo

Cuando tenemos dos cargas positivas situadas a una cierta distancia, el campo eléctrico en el segmento entre ellas es la suma de dos campos que van en sentidos opuestos. Si estamos cerca de la carga 1, el campo de ésta domina y la resultante va en el sentido que se aleja de ella. Si nos acercamos a la carga 2, ocurre lo mismo con la 2 y el campo resultante va hacia fuera de ésta. En algún punto intermedio los dos campos tienen la misma intensidad y el campo resultante es nulo.

Si las dos cargas son negativas, el razonamiento es idéntico, salvo que el sentido de los campos indiviudales es el contrario.

Cargas iguales

En el primer caso tenemos dos cargas iguales. Por simetría, el punto de anulación es A, el punto medio entre ambas, para el cual ya calculamos previamente que el campo se anula.

$q_{1}=q_{2}=1\,\mathrm {nC} \qquad \Rightarrow \qquad {\vec {E}}({\vec {0}})={\vec {0}}$

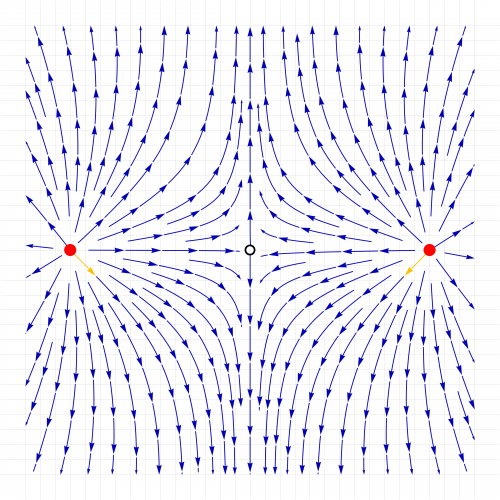
Cargas desiguales

Si las cargas son de diferente magnitud, ya el punto medio no es de campo nulo, ya que es más intenso el campo de la carga mayor. Para encontrar un punto en el que se anule el campo debemos acercarnos a la carga más pequeña, de manera que su menor magnitud se compense con una menor distancia.

Si la carga $q_{1}$ se encuentra en el punto $-a{\vec {\imath }}$ y la carga $q_{2}$ en $+a{\vec {\imath }}$, el punto de campo nulo estará en algún punto P de posición $x{\vec {\imath }}$ con x en el intervalo $-a<x<a$. La distancia a las cargas es

$r_{1}=x-(-a)=a+x\qquad \qquad r_{2}=a-x$

de forma que el campo en P es

${\vec {E}}_{P}={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q_{1}}{(a+x)^{2}}}{\vec {\imath }}+{\frac {q_{2}}{(a-x)^{2}}}(-{\vec {\imath }})\right)$

Si imponemos que el campo en este punto sea nulo llegamos a la ecuación

${\frac {q_{1}}{(a+x)^{2}}}-{\frac {q_{2}}{(a-x)^{2}}}=0\qquad \Rightarrow \qquad {\frac {(a-x)^{2}}{(a+x)^{2}}}={\frac {q_{2}}{q_{1}}}$

Sustituyendo las cargas en nanoculombios y las distancias en centímetros y hallando la raíz cuadrada

${\frac {(12-x)^{2}}{(12+x)^{2}}}={\frac {9}{1}}=9\qquad \Rightarrow \qquad {\frac {12-x}{12+x}}=3$

Esto nos da la ecuación de primer grado

$12-x=36+3x\qquad \Rightarrow \qquad x=-6\,\mathrm {cm}$

El resultado anterior nos dice que al ser la segunda carga 9 veces más grande que la primera, la posición de equilibrio debe estar al triple de distancia de ella que de la primera. Esto nos da una posición de equilibrio que se encuentra dividiendo el intervalo total en 4 partes iguales. El punto está a 1/4 de la primera carga y 3/4 de la segunda.

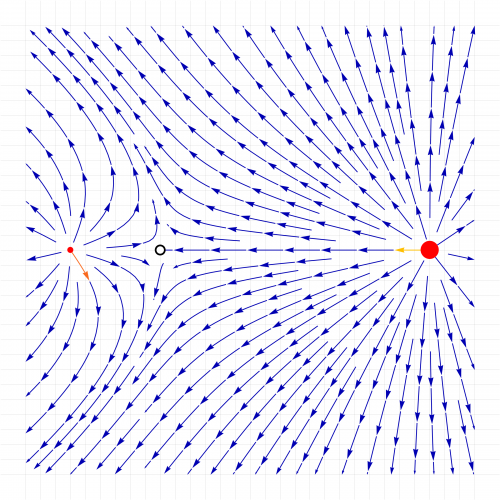
Cargas de signo opuesto

En el caso de dos cargas de signo opuesto, en el segmento entre las dos cargas el campo va en el mismo sentido, por lo que no puede anularse el campo total. Sin embargo, sobre la recta que pasa por las cargas, pero por el exterior del segmento, los campos de cada carga van en sentidos contrarios, por lo que puede conseguirse la anulación.

Como en el caso de cargas del mismo signo, la posición de campo nulo estará más cerca de la carga más pequeña.

Cargas de la misma magnitud

En el caso de dos cargas de la misma magnitud y signo contrario, no existe ningún punto en el que el campo se anule (es el único caso de dos cargas en que esto ocurre). Para que ello ocurriera, el punto debería estar a la misma distancia de las dos cargas, pero por el exterior del segmento, lo que es imposible.

Para verlo analíticamente, supongamos que el punto de equilibrio se encuentra a una distancia x de la posición de equilibrio por el lado x > a. Las distancias a las dos cargas son

$r_{1}=x+a\qquad \qquad r_{2}=x-a\qquad \qquad {\vec {u}}_{r1}={\vec {u}}_{r2}={\vec {\imath }}$

El campo total en este punto es

${\vec {E}}_{P}={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q_{1}}{(a+x)^{2}}}{\vec {\imath }}+{\frac {(-q_{1})}{(x-a)^{2}}}({\vec {\imath }})\right)$

y para que se anule debe cumplirse, sacando factor común,

${\frac {1}{(x+a)^{2}}}-{\frac {1}{(x-a)^{2}}}=0\qquad \Rightarrow \qquad x-a=x+a$

que no tiene solución.

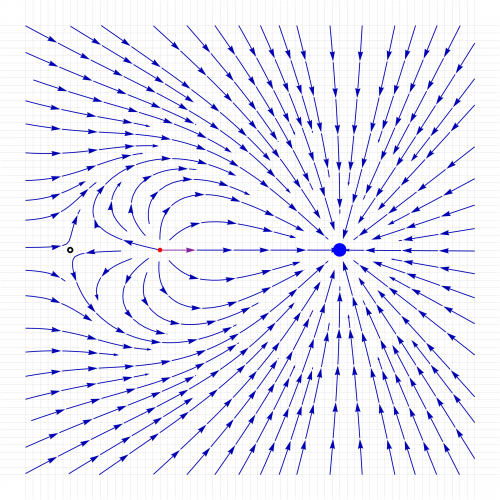
Cargas de diferente magnitud

Si las cargas son de distinta magnitud, sí existe punto en el que se anule el campo. En el caso del problema, en que la segunda carga vale $q_{2}=-9q_{1}$, el punto de campo nulo estará más cerca de $q_{1}$ a una distancia que sea 1/3 de la distancia a $q_{2}$. Analíticamente, si el punto está en $-s{\vec {\imath }}$ tenemos las distancias y vectores unitarios

$r_{1}=s-a\qquad \qquad r_{2}=s+a\qquad \qquad {\vec {u}}_{r1}={\vec {u}}_{r2}=-{\vec {\imath }}$

siendo la suma de los dos campos

${\vec {E}}_{P}={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q_{1}}{(s-a)^{2}}}(-{\vec {\imath }})+{\frac {(-|q_{2}|)}{(s+a)^{2}}}(-{\vec {\imath }})\right)$

que nos da la ecuación

${\frac {1}{(s-12)^{2}}}-{\frac {9}{(s+12)^{2}}}=0\qquad \Rightarrow \qquad s=24\,\mathrm {cm}$

El punto de campo nulo es entonces

${\vec {r}}_{P}=-24\,{\vec {\imath }}\,(\mathrm {cm} )$

que está a una distancia de 12 cm de la primera carga y 36 de la segunda.

Resumen

Reuniendo los cuatro resultados

$q_{1}$ (nC)	${\vec {r}}_{2}$ (cm)	$q_{2}$ (nC)	${\vec {r}}_{1}$ (cm)	${\vec {E}}=0$ en…
+1	$-12{\vec {\imath }}$	+1	$+12{\vec {\imath }}$	${\vec {0}}$
+1	$-12{\vec {\imath }}$	+9	$+12{\vec {\imath }}$	$-6{\vec {\imath }}$
+1	$-12{\vec {\imath }}$	-1	$+12{\vec {\imath }}$	No se anula
+1	$-12{\vec {\imath }}$	-9	$+12{\vec {\imath }}$	$-24{\vec {\imath }}$