Fuerza entre cargas en un triángulo

Enunciado

Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado b. Calcule la fuerza eléctrica sobre cada una de ellas.

Suponga que se cambia una de las cargas +q por una carga −q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas?

Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una?

Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza?

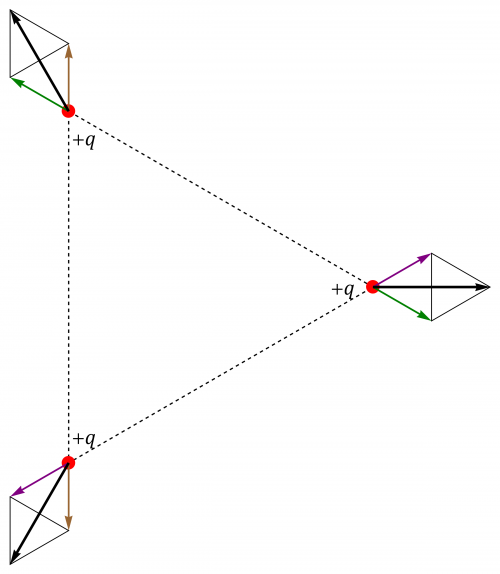
Tres cargas positivas

Por la simetría del sistema, es claro que las tres cargas van a experimentar la misma fuerza en módulo, pero la dirección será diferente para cada una. Este problema puede hacerse separando por componentes y empleando todo el álgebra vectorial, pero es más sencillo empleando un poco de geometría.

Tenemos las tres cargas formando un triángulo equilátero. Cada una de ellas ejerce una fuerza sobre cada una de las otras que tendrá por módulo

$F_{0}={\frac {1}{4\pi \varepsilon _{0}}}\,{\frac {q^{2}}{b^{2}}}$

con dirección a lo largo de los lados y sentido hacia el exterior, ya que las cargas se repelen entre sí.

Cuando consideramos la fuerza neta sobre una de las cargas, vemos que es la suma de dos vectores del mismo módulo y que forman un ángulo de 60° entre ellos. La suma vectorial tiene un módulo igual al de cada uno de ellos multiplicado por 2 veces el coseno de 30°, es decir

$\left|{\vec {F}}_{1}\right|=2\cos(30^{\circ })F_{0}={\sqrt {3}}F_{0}$

y la dirección de la fuerza sobre cada carga será radial desde el centro del triángulo.

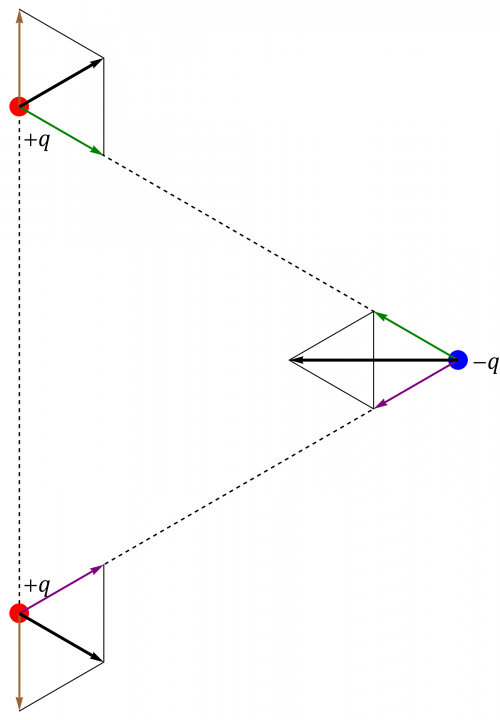
Dos cargas positivas y una negativa

Cuando una de las cargas es negativa, se invierte el sentido de las fuerzas que ella ejerce y las que actúan sobre ella.

La fuerza sobre la carga negativa será entonces la misma en módulo que la calculada en el apartado anterior, pero sentido opuesto.

La fuerza sobre cada carga positiva será la suma vectorial de dos fuerzas de módulo $F_{0}$ pero que ahora forman un ángulo de 120°. La resultante es una fuerza del mismo módulo $F_{0}$ formando un ángulo de 60° con el lado del triángulo.

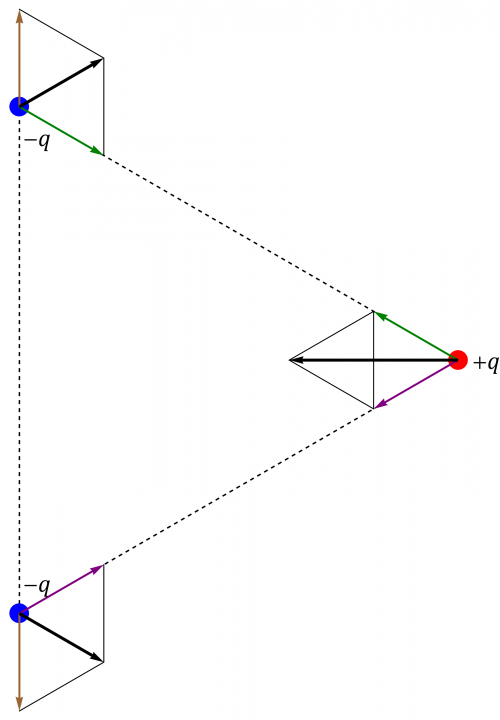
Dos cargas negativas y una positiva

Si cambiamos una segunda carga, pasamos a tener dos cargas negativas y una positiva, pero esto es lo mismo que si el apartado anterior, cambiamos el signo de las tres cargas. Puesto que en la ley de Coulomb aparece el producto de las cargas, si cambiamos el signo de las dos, el resultado no cambia. Por tanto, las fuerzas en este caso son las mismas que en el apartado anterior. Ahora la carga positiva experimenta una fuerza de módulo ${\sqrt {3}}F_{0}$ y las dos negativas una de módulo $F_{0}$.

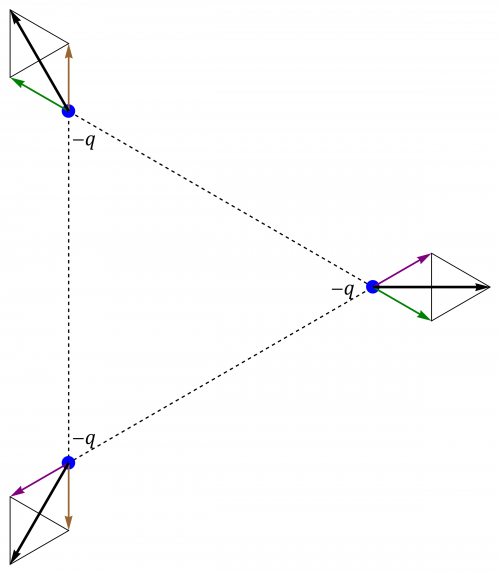
Tres cargas negativas

Si tenemos las tres cargas iguales y negativas, la fuerza sobre cada una de ellas será la misma que en el primer apartado: una fuerza de módulo ${\sqrt {3}}F_{0}$ en la dirección radial desde el centro del triángulo.