Cargas en los vértices de un cuadrado (GIOI)

Enunciado

Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide 20 cm, según ilustra la figura. Los valores de todas las cargas son +10 nC o −10 nC

1. ¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado?
2. ¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito?
3. Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema?
4. ¿Qué trabajo hay que realizar para permutar una carga positiva por una negativa vecina?

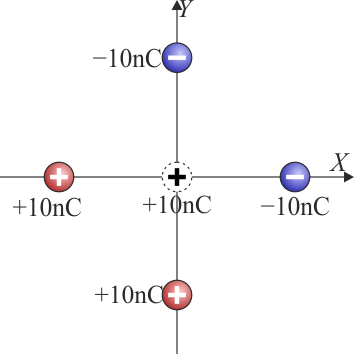
Fuerza sobre una carga central

El par de cargas situadas sobre el eje Z produce una fuerza neta en el sentido del eje X positivo. Las dos cargas sobre el eje Y una fuerza igual en el sentido del eje Y. La fuerza total tendrá entonces iguales componentes en los dos ejes e irá en el sentido del primer cuadrante. Esto reduce las posibles respuestas a la B o a la D. Para saber cuál es la correcta debemos aplicar la ley de Coulomb.

La fuerza debida a la carga situada en la parte negativa del eje X es

${\vec {F}}_{1}={\frac {1}{4\pi \varepsilon _{0}}}\,{\frac {q_{1}q_{0}}{d^{2}}}{\vec {\imath }}=9\times 10^{9}{\frac {(10^{-8})^{2}}{(0.1)^{2}}}{\vec {\imath }}\,\mathrm {N} =90{\vec {\imath }}\,\mu \mathrm {N}$

La debida a la carga situada en la parte positiva del eje X es igual a esta. Las de las cargas en el eje Y iguales pero en el sentido de $+{\vec {\jmath }}$. Por tanto, la fuerza neta es

${\vec {F}}=180({\vec {\imath }}+{\vec {\jmath }})\,\mu \mathrm {N}$

Trabajo para mover la carga

El punto central se encuentra en una posición simétrica respecto a las dos cargas de la misma magnitud y signo opuesto situadas en el eje Z. Lo mismo ocurre con las del eje Y. Por tanto, el potencial al que se encuentra la carga es nulo

$V({\vec {0}})={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{d}}+{\frac {-q}{d}}+{\frac {q}{d}}+{\frac {-q}{d}}\right)=0$

Dado que el infinito también se encuentra a potencial nulo, el trabajo para ir de un punto a otro es cero.

$W_{\mathrm {in} }=q\,\Delta V=q(0-0)=0$

El subíndice "in" quiere decir que este es un trabajo externo que se realiza 'sobre' el sistema.

Energía almacenada

Cada carga se encuentra sometido al potencial de dos cargas opuestas situadas simétricamente (cuyos potenciales respectivos se anulan) y de una de signo opuesto, que produce una energía potencial negativa.

Podemos hallar el valor de la energía.

$U_{\mathrm {e} }={\frac {1}{2}}\sum _{i}q_{i}V'({\vec {r}}_{i})$

siendo $V'({\vec {r}}_{i})$ el potencial en cada carga debido al resto de cargas del sistema. Para la carga del eje X negativo vale

$q_{1}=q=10^{-8}\mathrm {C} \qquad \qquad V'_{1}={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{d{\sqrt {2}}}}-{\frac {q}{2d}}-{\frac {q}{d{\sqrt {2}}}}\right)=-{\frac {1}{4\pi \varepsilon _{0}}}\,{\frac {q}{2d}}=-450\,\mathrm {V}$

Lo que da una contribución para esta carga

${\frac {1}{2}}q_{1}V'_{1}=-{\frac {q^{2}}{16\pi \varepsilon _{0}d}}=-2.25\,\mu \mathrm {J}$

Operando igualmente para las otras tres cargas obtenemos

$U_{\mathrm {e} }={\frac {1}{2}}\times 4\times \left(-{\frac {q^{2}}{8\pi \varepsilon _{0}d}}\right)=-{\frac {q^{2}}{4\pi \varepsilon _{0}d}}=-{\frac {9\times 10^{9}\times (10^{-8})^{2}}{0.1}}=-9\,\mu \mathrm {J}$

Trabajo para permutar cargas

A la hora de calcular el trabajo para permutar dos cargas, podemos hacerlo de dos formas:

• A partir de la diferencia entre la energía final y la inicial
• Calculando el trabajo en un proceso que lleve del estado inicial al final.

En el primer caso, ya tenemos la energía inicial

$U_{\mathrm {eA} }=-9\,\mu \mathrm {J}$

La energía final se calcula observando que en esa situación cada carga tiene como cargas contiguas dos del signo opuesto y enfrente una del mismo signo. Por tanto, para cada carga

${\frac {1}{2}}q_{1}V'_{1}={\frac {1}{8\pi \varepsilon _{0}}}\left(2\left({\frac {-q^{2}}{d{\sqrt {2}}}}\right)+{\frac {q^{2}}{2d}}\right)=-4.11\,\mu \mathrm {J}$

como las cuatro cargas están en la misma situación, la energía total final es

$U_{\mathrm {eB} }=4\times (-4.11\,\mu \mathrm {J} )=-16.5\,\mu \mathrm {J}$

y por tanto, el trabajo necesario para realizar la permuta es

$W_{\mathrm {in} }=U_{\mathrm {eB} }-U_{\mathrm {eA} }=-16.5\,\mu \mathrm {J} +9\,\mu \mathrm {J} =-7.5\,\mu \mathrm {J}$