Enunciado
Calcule la carga total de las siguientes distribuciones de carga:
 N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en .
N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en . Un anillo circular de radio b con una densidad lineal de carga uniforme .
Un anillo circular de radio b con una densidad lineal de carga uniforme . Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX.
Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX. Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga .
Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga . Una esfera maciza de radio b con densidad de carga uniforme .
Una esfera maciza de radio b con densidad de carga uniforme . Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Cargas en un polígono
El primer caso es trivial. Puesto que las cargas se pueden sumar, la carga total será la suma de las N cargas individuales
Anillo cargado uniformemente
En el caso de un anillo el principio es el mismo, solo que en lugar de una suma tenemos una integral
Para una densidad lineal de carga, la carga de un elemento es
En este caso la densidad de carga es uniforme, por lo que puede salir de la integral
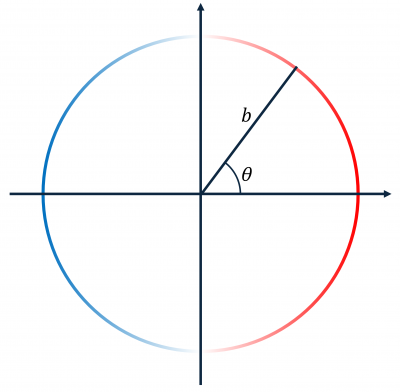
Anillo cargado no uniformemente
En el siguiente caso la densidad es no uniforme y por ello es necesario realizar la integración.
Si etiquetamos los puntos del anillo por la variable θ la longitud de un arco diferencial es igual al producto del radio por el ángulo
y el cálculo de la carga se convierte en
La carga total es cero porque la integral del coseno sobre un periodo completo se anula. Esto expresa físicamente el que el coseno, y por tanto la carga, es positiva en una mitad del anillo (primer y cuarto cuadrantes) y negativa en la otra mitad (segundo y tercer cuadrantes) y po cada elemento de carga positivo hay uno negativo que lo anula.
Superficie esférica cargada uniformemente
En este caso debemos integrar sobre toda la superficie
Como en el caso del anillo cargado uniformemente, la densidad de carga sale de la integral
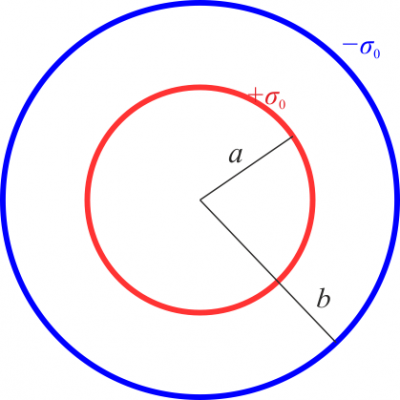
Dos esferas concéntricas
La carga total es la suma de la que hay en cada una de las esferas. A su vez, por ser la densidad uniforme en cada una de ellas
siendo la carga total
Esfera maciza cargada
En el caso de una distribución volumétrica de carga, la carga total se halla mediante una integral de volumen
donde la integral se extiende a toda la región donde haya carga. En este caso el volumen es una esfera y la densidad de carga en ella es independiente de la posición por lo que
Esfera cargada no uniformemente
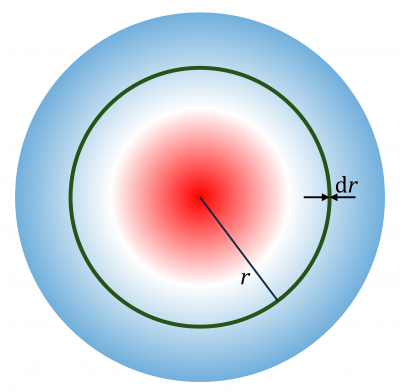
En el último caso tenemos una esfera cuya densidad de carga es positiva entre 0 y R/2, y negativa entre R/2 y R. La carga neta no es nula, ya que la región ocupada por la carga negativa es mayor que la positiva. Si la distribución de carga no es uniforme, sino que depende de la posición, es necesario hallar la integral de volumen
Dividiemos la esfera en finas capas concéntricas. El volumen de cada capa es su área multiplicada por su espesor
En cada una de ellas la densidad de carga es uniforme. La carga (diferencial) de cada capa es
\mathrm{d}q=\rho(r)\,\mathrm{d}v = A(b-r)(4\pi r^2)\mathrm{d}r
y la carga total de la esfera
Resulta una carga neta negativa porque la región ocupada por la carga negativa es más extensa.






















