Campo de un anillo homogéneo (GIOI)

Enunciado

Calcule, por integración directa, el campo eléctrico en los puntos del eje de un anillo de radio b que almacena una carga Q distribuida uniformemente.

Solución

Calculamos el campo eléctrico empleando el principio de superposición. Consideramos el anillo formado por pequeños elementos de carga, cada una de los cuales produce una contribución diferencial al campo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{\mathrm{d}q(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}}

siendo

• Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}} la posición del punto P donde queremos hallar el campo,
• ${\vec {r}}^{\,\prime }$ la posición de los puntos donde se hallan las cargas
• $({\vec {r}}-{\vec {r}}^{\,\prime })$ la posición relativa de P al elemento de carga
• Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\vec{r}-\vec{r}^{\,\prime}|} la distancia de P al elemento de carga

En el caso del anillo con una carga uniformemente distribuida, dividimos el anillo en segmentos de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}l=R\,\mathrm{d}\theta'} , cada uno de los cuales tiene una carga

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}q = \lambda\,\mathrm{d}\ell=\frac{Q}{L}\mathrm{d}\ell = \frac{Q}{2\pi b}b\mathrm{d}\theta'=\frac{Q}{2\pi}\mathrm{d}\theta'}

La posición del punto P donde queremos hallar el campo es un punto del eje

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}=z\vec{k}}

y la de los elementos de carga, en función del ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta'}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}=b\cos(\theta')\vec{\imath}+b\,\mathrm{sen}(\theta')\vec{\jmath}}

La posición relativa es la diferencia de estos dos vectores

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}-\vec{r}^{\,\prime}=-b\cos(\theta')\vec{\imath}-b\,\mathrm{sen}(\theta')\vec{\jmath}+z\vec{k}}

La distancia entre cada punto del anillo y un punto del eje es la misma para todos ellos. Por el teorema de Pitágoras

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\vec{r}-\vec{r}^{\,\prime}| = \sqrt{b^2+z^2}}

Llevamos todo esto a la expresión integral y sacamos factor común todo aquello que sea constante de cara a la integral. Esto nos da

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{E}(z\vec{k})=\frac{1}{4\pi\varepsilon_0}\int_L \frac{\mathrm{d}q'(\vec{r}-\vec{r}^{\,\prime})}{|\vec{r}-\vec{r}^{\,\prime}|^3}=} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle =\frac{Q}{(4\pi\varepsilon_0)(2\pi)(b^2+z^2)^{3/2}}\left(-b\vec{\imath}\int_0^{2\pi}\cos(\theta')\mathrm{d}\theta'-b\vec{\jmath}\int_0^{2\pi}\mathrm{sen}(\theta')\mathrm{d}\theta'+z\vec{k}\int_0^{2\pi}\mathrm{d}\theta'\right)}

Esta integral parece muy complicada, pero en realidad es muy sencilla. Se reduce a calcular tres integrales inmediatas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \int_0^{2\pi}\cos(\theta')\mathrm{d}\theta'=0\qquad\qquad \int_0^{2\pi}\mathrm{sen}(\theta')\mathrm{d}\theta'=0\qquad\qquad \int_0^{2\pi}\mathrm{d}\theta'=2\pi}

La anulación de las dos primeras integrales expresa que, en un anillo las componentes horizontales del campo debido a un elemento de carga se anulan con las del punto diametralmente opuesto, quedando solo las componentes verticales.

El resultado final es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{E}(z\vec{k})=\frac{Qz}{4\pi\varepsilon_0(b^2+z^2)^{3/2}}\vec{k}}

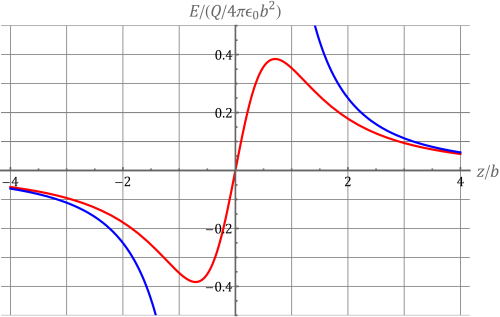
Si representamos la componente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_z} del campo como función de la distancia al plano del anillo, obtenemos que en el punto central el campo es nulo, y que también se anula en puntos muy alejados del él, pero a distancias intermedias crece hasta un valor máximo. El sentido del campo es siempre alejándose del anillo (suponiendo su carga positiva) lo que se manifiesta en que el signo de la componente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_z} es positiva para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z> 0} y negativa para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle z < 0}

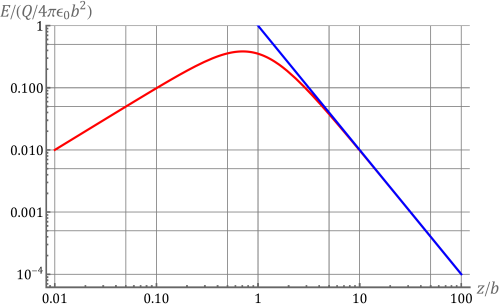
Podemos comparar este campo con el de una carga puntual. Esto se ve más claro si se usa una escala log-log, es decir, en el eje X los puntos se escalan como el logaritmo de la distancia y en el eje Y como el logaritmo del campo. En este tipo de gráfica el campo de una carga puntual se reduce a una línea recta de pendiente -2 (por la dependencia con la inversa del cuadrado de la distancia). El campo del anillo es diferente para distancias pequeñas pero para distancias iguales o superiores a 10 veces el radio ya es prácticamente indistinguible del de una carga puntual