Problemas de Movimiento relativo (MR G.I.C.)

Problemas del boletín

Giro de un triedro

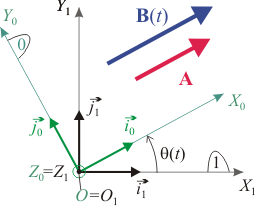
Los triedros $O_{1}X_{1}Y_{1}Z_{1}$ y $OX_{0}Y_{0}Z_{0}$ están definidos de modo que sus orígenes y los ejes $O_{1}Z_{1}$ coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme ${\vec {\omega }}_{01}=\omega \,{\vec {k}}_{1}=\omega \,{\vec {k}}_{0}$, de modo que el ángulo $\theta$ indicado en la figura es $\theta =\omega \,t$.

1. Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1".
2. Dado el vector ${\vec {A}}(t)=a\,{\vec {\imath }}_{0}$ calcula

$\left.{\dfrac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{1}\qquad \qquad \left.{\dfrac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{0}$

1. Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1").
2. Haz el mismo cálculo para el vector ${\vec {B}}(t)=b\,t\,{\vec {\imath }}_{0}$

Coche sobre una plataforma circular

Una plataforma circular gira alrededor de un eje perpendicular a ella que pasa por su centro con velocidad angular uniforme $\omega$. Un coche se mueve radialmente desde el centro de la plataforma hacia fuera con velocidad uniforme $v_{c}$. Encuentra la expresión de la velocidad del coche visto desde la plataforma y desde un observador en reposo absoluto. Describe las trayectorias que describe el coche para cada uno de estos observadores.

Ayuda

${\begin{array}{ccc}\displaystyle \int t\,\,\mathrm {sen} \,(\omega t)\mathrm {d} t=-{\dfrac {t}{\omega }}\cos(\omega t)+{\dfrac {1}{\omega ^{2}}}\,\mathrm {sen} \,(\omega t)&\qquad &\displaystyle \int t\,\cos(\omega t)\mathrm {d} t={\dfrac {t}{\omega }}\,\mathrm {sen} \,(\omega t)+{\dfrac {1}{\omega ^{2}}}\cos(\omega t)\end{array}}$

Disco engarzado en otro disco

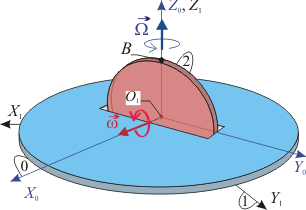
En la figura se muestra un disco de radio $R$ (sólido "2"), que gira con velocidad angular $\omega _{20}(t)=\omega$, constante, alrededor del eje perpendicular a él, $O_{1}X_{0}$. Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante $\omega _{01}(t)=\Omega$, alrededor del eje vertical $O_{1}Z_{1}$ de un sistema de referencia fijo $O_{1}X_{1}Y_{1}Z_{1}$ (sólido "1"). Determina las magnitudes cinemáticas ${\vec {v}}_{21}^{B}$ y ${\vec {a}}_{21}^{B}$ en el instante representado en la figura.

Disco y varilla con dos rotaciones

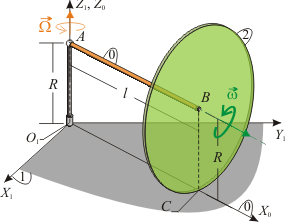
El sistema de la figura está formado por una varilla $AB$ de longitud $l$ (sólido "0"), cuyo extremo $A$ está fijado en el eje vertical $O_{1}Z_{1}$, a una altura $R$ sobre el plano horizontal fijo $O_{1}X_{1}Y_{1}$ (sólido "1"). La varilla $AB$ gira alrededor de $O_{1}Z_{1}$ con una velocidad angular constante $\Omega$, permaneciendo siempre perpendicular a dicho eje vertical fijo. El extremo $B$ del sólido "0" está articulado al centro de un disco de radio $R$ (sólido "2"), de modo que la varilla es siempre perpendicular al disco. El disco gira con una velocidad angular constante $\omega$, coincidiendo su eje de giro con la varilla.

1. Caracterice los movimientos {01}, {20} y {21} (reducciones cinemáticas).
2. Obtenga la expresión de la velocidad ${\vec {v}}_{21}^{C}$ del punto de contacto del disco con el plano fijo $O_{1}X_{1}Y_{1}$, (punto $C$) en términos de los datos del problema. ¿Qué relación debe existir entre las velocidades angulares $\omega$ y $\Omega$ para que el disco ruede sin deslizar sobre el plano?
3. Obtenga las expresiones de la aceleración angular del movimiento {21} y de la aceleración ${\vec {a}}_{21}^{B}$ del centro del disco (punto $B$). Calcule la aceleración del punto de contacto $C$ perteneciente al disco cuando éste rueda sin deslizar sobre el plano $O_{1}X_{1}Y_{1}$.

Varilla rotando con extremo deslizando sobre un eje

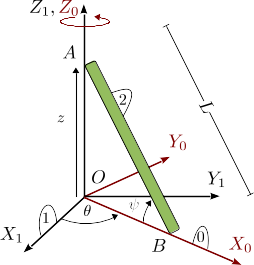
El extremo $A$ de una barra de longitud $L$ desliza sobre el eje $OZ_{1}$. La barra gira respecto al eje $OZ_{1}$, de modo que está siempre contenida en el plano $OX_{0}Z_{0}$ y el punto $B$ permanece siempre en el eje $OX_{0}$. El plano $OX_{0}Z_{0}$ realiza una rotación de eje permanente $OZ_{0}$. En el instante inicial el punto $A$ coincidía con $O$ y el punto $B$ estaba sobre el eje $OX_{1}$.

1. Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas. El resultado debe quedar en función de $z$, $\psi$, $\theta$ y sus derivadas temporales.
2. Supongamos que la velocidad del punto $A$ respecto al eje es constante y de magnitud $v_{0}$. Encuentra la ecuación diferencial que determina la función $\psi (t)$.

Cono rodando sin deslizar sobre plano

Un cono recto de radio $R$ en su base y una altura $h={\sqrt {3}}\,R$ (sólido “2”), se mueve rodando sin deslizar sobre el plano fijo $O_{1}X_{1}Y_{1}$ (sólido “1”), en el cuál apoya, en cada instante, una generatriz ${\overline {OG}}$. La velocidad del centro $C$ de la base del cono, medida desde el sistema de referencia ligado al sólido “1”, tiene módulo constante de valor $v_{0}$. Para facilitar la descripción del movimiento, se introduce un sistema de referencia $OX_{0}Y_{0}Z_{0}$ (sólido “0”) con origen $O$ en el vértice del cono, el eje $OZ_{0}$ siempre perpendicular al plano fijo “1”, y cuyo eje $OY_{0}$ contiene en cada instante a la generatriz del cono en contacto con dicho plano.

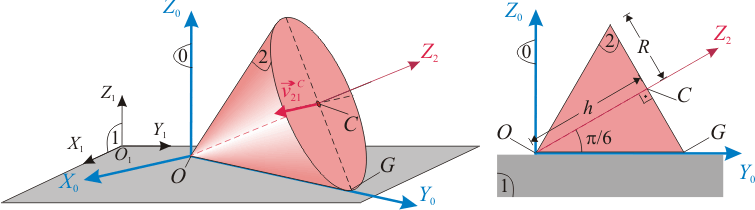
1. Reducciones cinematicas de los movimientos relativos.
2. Ejes de rotación y naturaleza de los movimientos.
3. Campos de aceleraciones.

Horquilla y disco

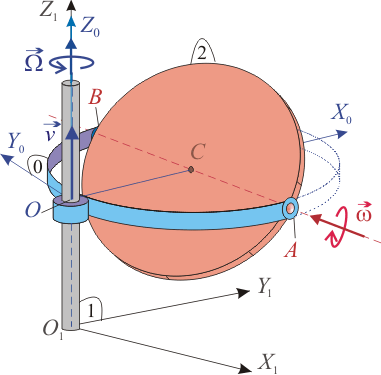
El sistema de la figura consiste en una horquilla semicircular (sólido "0"), que siempre está paralela al plano fijo $O_{1}X_{1}Y_{1}$ (sólido "1"). El punto $O$ de dicho aro (siempre el mismo) se desplaza con velocidad $v$ sobre el eje $O_{1}Z_{1}$, a la vez que el aro gira con velocidad angular constante $\Omega$ alrededor de dicho eje fijo. Un disco de radio $R$ (sólido "2"), se mueve respecto a "0" girando alrededor del diámetro común $AB$, con velocidad angular constante $\omega$.

Nota: Los valores de $\Omega$, $\omega$ y $v$ pueden ser positivos o negativos.

1. ¿Cuándo es nula la velocidad mínima del movimiento {21}?
2. Qué debe ocurrir para que el eje instantáneo de rotación y mínimo deslizamiento pase por el centro del disco? Calcule en este caso la derivada temporal de la reducción cinemática
3. ¿Qué condición debe cumplirse para que el movimiento {21} sea una rotación instantánea y el eje instantáneo de rotación pase por el centro del disco?

Partícula en tubo que gira (ecuaciones de movimiento)

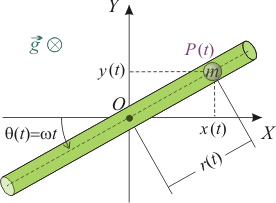
Una partícula de masa $m$ se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme $\omega$ en torno a un eje perpendicular al del tubo. Obtenga las ecuaciones de movimiento para la partícula aplicando los resultados del movimiento relativo de sólidos rígidos.

Otros problemas

Movimiento relativo de un coche y un tren

Un tren circula por una vía recta con velocidad uniforme $v_{t}$. Un coche se aleja de un paso a nivel perpendicularmente al tren con velocidad $v_{c}$. Encuentra la velocidad del coche vista por un observador que se mueve con el tren y por un observador en el paso a nivel. Describe las trayectorias que describe el coche para cada uno de estos observadores.

Hélice de un avión que gira

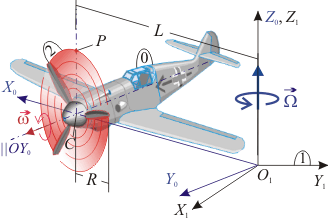
El avión (sólido "0") de la figura se mueve de modo que el centro $C$ de su hélice describe una circunferencia de radio $L$. La velocidad angular de este giro es uniforme y su módulo es $|{\vec {\omega }}_{01}|=\Omega$. Además, la hélice (sólido "2"), cuyo radio es $R$, gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad también uniforme y de módulo $|{\vec {\omega }}_{20}|=\omega$. Se pide

1. La reducción cinemática de los movimientos {01} y {20}.
2. Aplicando la composición de velocidades, la velocidad ${\vec {v}}_{21}^{P}$ y aceleración ${\vec {a}}_{21}^{P}$ del punto más alto de la hélice (punto $P$ en la figura).
3. La reducción cinemática del movimiento {21} en $P$ y la ecuación del E.I.R.M.D. ¿Qué tipo de movimiento describe la hélice respecto al sólido "1"?
4. Calcule numéricamente $|{\vec {v}}_{21}^{P}|$ y $|{\vec {a}}_{21}^{P}|$ para los valores $R=1\,\mathrm {m}$, $L=100\,\mathrm {m}$, $\omega =100\,\mathrm {rad/s}$ y $\Omega =1\,\mathrm {rad/s}$.

Nota: Se recomienda utilizar el triedro asociado al sólido "0" para resolver el problema.

Dos conos en movimiento relativo

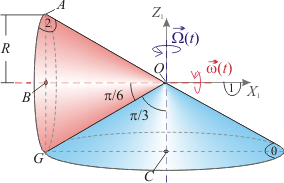
Dos conos rectos de semiángulos en el vértice $\pi /3$ y $\pi /6$ (sólidos "0" y "2", respectivamente), se hallan en contacto en todo instante por una generatriz. Cada cono realiza un movimiento de rotación permanente respecto a un sistema de referencia fijo (sólido "1") alrededor de su correspondiente eje de simetría. Las velocidades angulares respectivas son ${\vec {\Omega }}(t)$ para el movimiento {01} y ${\vec {\omega }}(t)$ para el {21}. Además, los conos se mueven de manera que sus puntos en contacto no tienen deslizamiento relativo.

1. ¿Que tipo de movimiento es el {20}?
2. En ese movimiento, ¿que puntos tienen velocidad mínima?
3. ¿Que relación deben cumplir las velocidades angulares del enunciado?
4. Calcula la aceleración angular ${\vec {\alpha }}_{20}$.

Esfera sobre dos raíles

Una esfera de radio $R$ (sólido "2"), se desplaza sobre dos carriles circulares concéntricos fijos de radios $R$ y $2R$ (sólido "1"), situados en un plano horizontal (ver figura). El movimiento de la esfera es tal que: i) en todo instante, rueda sin deslizar sobre ambos carriles, y ii) su centro $C$ realiza un movimiento circular uniforme, siendo $v_{0}$ el módulo de su velocidad. Considerando cómo sólido móvil intermedio (sólido "0") al plano $O_{1}X_{0}Z_{0}$ que contiene en todo instante al centro $C$ de la esfera (ver figura), calcula:

1. Los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
2. Reducciones cinemáticas de dichos movimientos,
3. Para el punto de la esfera en contacto con el carril de mayor diámetro (punto $B$), los vectores ${\vec {v}}_{20}^{B}$ y ${\vec {a}}_{21}^{B}$

Cuestión sobre sólidos en contacto

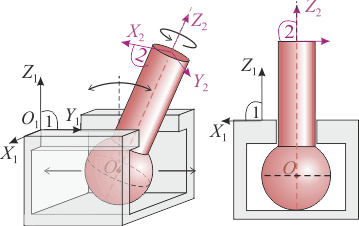
Los sólidos rígidos de la figura se encuentran en contacto, por lo que su movimiento relativo está sometido a ciertas restricciones. El extremo esférico del sólido “2” está obligado a permanecer en el interior del carril (sólido “1”), pudiendo desplazarse sólo a lo largo de su dirección longitudinal (paralela al eje $O_{1}Y_{1}$). Por otra parte, el sólido “2” no puede ejecutar giros en torno a dicha dirección debido a que el vástago cilíndrico está insertado en la ranura del sólido “1”.

1. Obtenga razonadamente el par cinemático (reducción cinemática en $O$) que describe de forma general el movimiento instantáneo permitido al sólido “2” respecto del carril (sólido “1”).
2. ¿Cuál es el número de grados de libertad del sistema? Justifique su respuesta.

Disco y vástago

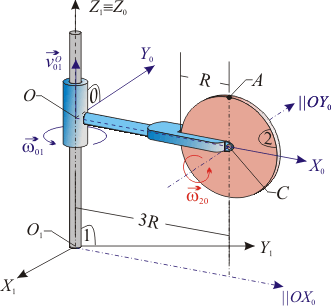
El sólido rígido "0" del mecanismo de la figura corresponde a un vástago $OC$ de longitud $3R$ que, mediante un par cilíndrico situado en su extremo $O$, permanece en todo instante perpendicular al eje vertical fijo $O_{1}Z_{1}$ (sólido "1"). Dicho par de enlace permite que el vástago gire alrededor de $O_{1}Z_{1}$ con velocidad angular constante de módulo $|{\vec {\omega }}_{01}|=2\omega$ y en el sentido mostrado en la figura; a su vez, el extremo $O$ se desplaza sobre el eje vertical $O_{1}Z_{1}$ en sentido positivo y con velocidad constante, siendo el módulo de ésta $|{\vec {v}}_{01}^{O}|=v$. El extremo $C$ del sólido "0" está articulado al centro de un disco de radio $R$ (sólido "2"), siempre contenido en el plano vertical $OX_{0}Z_{0}$; el movimiento relativo del disco respecto del vástago consiste en una rotación permanente alrededor de un eje paralelo a $OY_{0}$ que pasa por $C$, en el sentido indicado en la figura y con velocidad angular constante de módulo $|{\vec {\omega }}_{20}|=\omega$. Utilizando la base vectorial del triedro ligado al sólido "0"- $OX_{0}Y_{0}Z_{0}$ - para expresar las magnitudes vectoriales, determina:

1. El vector rotación instantánea ${\vec {\omega }}_{21}$ y su derivada temporal ${\vec {\alpha }}_{21}$ (vector aceleración angular), correspondientes al movimiento del disco respecto al triedro fijo.
2. Las velocidades del punto $A$ del perímetro del disco en el instante en el que aquél ocupa el punto más alto del diámetro vertical(ver figura), para cada uno de los tres movimientos relativos que se distinguen en el mecanismo descrito: ${\vec {v}}_{01}^{A}$, ${\vec {v}}_{20}^{A}$ y ${\vec {v}}_{21}^{A}$.
3. Las aceleraciones ${\vec {a}}_{01}^{A}$, ${\vec {a}}_{20}^{A}$ y ${\vec {a}}_{21}^{A}$ para el mismo punto y en el mismo instante especificado en el apartado anterior.

Dos ventiladores

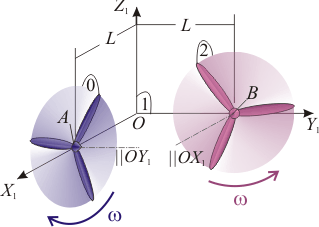
Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos "0" y "2") de orientación fija, ambos a la misma altura, y con sus respectivos centros ($A$ y $B$) equidistantes (distancia $L$) de la esquina (punto $O$). Los dos ventiladores rotan con velocidad angular de módulo constante e igual a $\omega$, con las orientaciones y sentidos dados en la figura. Definido el triedro fijo $OXYZ$ (sólido "1") del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determina:

1. Los vectores ${\vec {\omega }}_{20}$ y ${\vec {\alpha }}_{20}$. Los vectores ${\vec {v}}_{20}^{O}$ y ${\vec {a}}_{20}^{O}$.
2. El eje instantáneo de rotación.

Nota: Se recomienda usar el triedro "1" y su base vectorial para resolver el ejercicio.

Disco deslizando sobre hilo rotante

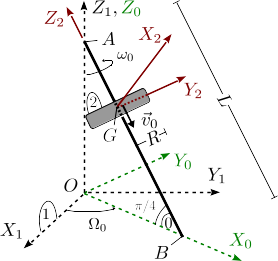
Un hilo rígido (sólido "0") de longitud $L$ rota alrededor del eje $OZ_{1}$ con velocidad angular constante $\Omega _{0}$, de modo que el punto $A$ está fijo y el punto $B$ describe una circunferencia sobre el plano $OX_{1}Y_{1}$. El hilo forma un ángulo $\pi /4$ con el plano $OX_{1}Y_{1}$. Un disco plano de masa $m$ y radio $R$ desliza por el hilo a la vez que rota alrededor de él con velocidad angular constante $\omega _{0}$. En el instante inicial el centro del disco estaba en el punto $A$. Se escoge un sólido "0" de modo que el plano $OX_{0}Z_{0}$ contiene siempre al hilo. El sistema "2", solidario con el disco, se escoge de modo que el eje $GZ_{2}$ coincide con su eje de simetría y el eje $GY_{2}$ es paralelo al eje $OY_{0}$. El punto $G$ del disco se mueve sobre el hilo con rapidez uniforme $v_{0}$, como se indica en la figura.

1. Calcula ${\vec {\omega }}_{21}$ y ${\vec {\alpha }}_{21}$.
2. Calcula la velocidad absoluta del punto $O_{1}$.
3. ¿Qué condición tiene que cumplirse para que el movimiento {21} sea una rotación pura en el instante inicial?
4. Supongamos que $\omega _{0}=0$. En este caso, el momento cinético del disco respecto de su centro de masas y su energía cinética en el instante en el que el punto $G$ está en el punto $B$.

Cilindro rodando sin deslizar

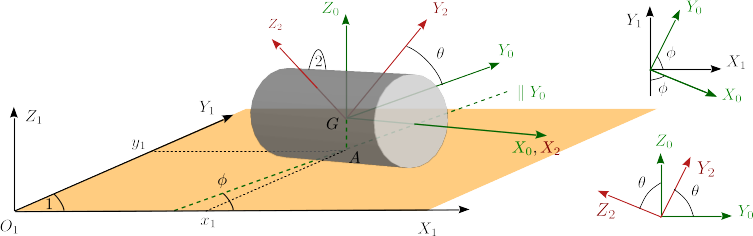
Un cilindro de radio $R$ (sólido "2") rueda sin deslizar sobre un plano fijo $O_{1}X_{1}Y_{1}Z_{1}$ (sólido "1"). Los ejes $GX_{2}Y_{2}Z_{2}$ son solidarios con el cilindro. Introducimos unos ejes auxiliares $GX_{0}Y_{0}Z_{0}$ que cumplen las siguientes propiedades: el $X_{0}$ es paralelo al eje del cilindro; el eje $Z_{0}$ es perpendicular al plano fijo "1"; el ángulo que forma el eje $Y_{0}$ con el eje $X_{1}$ es $\phi$. El punto $A$ señala el punto geométrico en la vertical de $G$ donde el cilindro está en contacto con el plano. Las coordenadas de este punto en los ejes "1" son $x_{1}$, $y_{1}$. Estas son también las coordenadas de $G$ en el plano fijo. Los diagramas auxiliares indican los ángulos relevantes entre los diferentes sistemas de ejes.

1. Encuentra la reducción cinemática en el punto $G$ de los movimientos {01}, {20}, {21}. Expresa los resultados en la base "0" y usa el menor número de coordenadas posible.

2. Si el tensor de inercia del cilindro en $G$ es de la forma

${\overleftrightarrow {I_{O}}}=\left[{\begin{array}{ccc}I_{1}&0&0\\0&I_{2}&0\\0&0&I_{2}\end{array}}\right]$

con $I_{1}$, $I_{2}$ conocidos, calcula el momento cinético del cilindro en $G$ y su energía cinética.

Problemas de sistemas de referencia no inerciales

Partícula girando en un aro

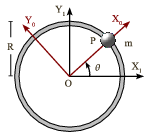
Una partícula describe un movimiento circular de radio $R$ con velocidad angular uniforme $\omega$. Se considera que no hay rozamiento ni peso.

1. Aplicando la Segunda Ley de Newton en el sistema en reposo, calcula la fuerza neta ejercida sobre la partícula en cada instante.
2. Se considera una escuadra $OX_{0}Y_{0}$, de modo que el eje $OX_{0}$ pasa siempre por el centro de la circunferencia y la posición de la partícula en cada instante. Aplica la Segunda Ley de Newton en este sistema de referencia no inercial.