Problemas de Cinemática del Sólido Rígido (GITI)

4.1. Estudio de la velocidad de tres puntos

En un hipotético sólido rígido, las posiciones y velocidades de tres puntos son respectivamente:

${\begin{array}{rclcrcl}{\overrightarrow {OA}}&=&{\vec {\imath }}&\qquad &{\vec {v}}^{A}&=&4{\vec {\imath }}+2{\vec {k}}\\{\overrightarrow {OB}}&=&{\vec {\jmath }}&\qquad &{\vec {v}}^{B}&=&2{\vec {\imath }}-2{\vec {\jmath }}-{\vec {k}}\\{\overrightarrow {OC}}&=&{\vec {k}}&\qquad &{\vec {v}}^{C}&=&2{\vec {\imath }}-{\vec {\jmath }}\end{array}}$

1. Demuestre que estas velocidades son compatibles con la condición de rigidez.
2. Halle la velocidad del punto $O(0,0,0)$.
3. Calcule la velocidad del punto ${\overrightarrow {OP}}=2{\vec {\imath }}-2{\vec {\jmath }}-{\vec {k}}$.
4. ¿Existe algún punto que tenga velocidad nula? ¿Dónde estaría situado?

Todas las cantidades están expresadas en las unidades del SI.

4.2. Ejemplo de campo de velocidades de un sólido

Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,

${\vec {v}}=(2+6y+3z){\vec {\imath }}+(3-6x-2z){\vec {\jmath }}+(1-3x+2y){\vec {k}}$

1. Pruebe que corresponde al movimiento de un sólido rígido.
2. Determine la velocidad angular y la velocidad de deslizamiento.
3. Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.

Todas las cantidades están expresadas en las unidades del SI.

4.3. Velocidad de tres puntos de un sólido

Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,

${\begin{array}{rclcrcl}{\overrightarrow {OA}}&=&{\vec {\imath }}+{\vec {k}}&\longrightarrow &{\vec {v}}^{A}&=&6{\vec {\imath }}+4{\vec {\jmath }}+a{\vec {k}}\\{\overrightarrow {OB}}&=&-{\vec {\imath }}+{\vec {\jmath }}&\longrightarrow &{\vec {v}}^{B}&=&b{\vec {\imath }}-{\vec {\jmath }}+2{\vec {k}}\\{\overrightarrow {OC}}&=&-{\vec {\jmath }}-{\vec {k}}&\longrightarrow &{\vec {v}}^{C}&=&4{\vec {\imath }}+c{\vec {\jmath }}+2{\vec {k}}\end{array}}$

1. Halle los valores de $a$, $b$, $c$.
2. Halle la velocidad del punto ${\overrightarrow {OP}}={\vec {\imath }}-{\vec {\jmath }}-{\vec {k}}$.
3. Calcule la velocidad angular y la de deslizamiento
4. Determine la posición del eje instantáneo de rotación.

Todas las cantidades están expresadas en las unidades del SI.

4.4. Sólido en rotación instantánea

Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto $A(1,0,-1)$ y lleva la dirección del vector ${\vec {e}}=2{\vec {\imath }}-2{\vec {\jmath }}-{\vec {k}}$, de tal forma que la velocidad del punto $B(0,2,1)$ es

${\vec {v}}^{B}=-4{\vec {\imath }}-6{\vec {\jmath }}+c{\vec {k}}$

1. Halle el valor de la constante $c$.
2. Calcule la velocidad angular instantánea.
3. Calcule la velocidad del punto $P(1,1,0)$.

Todas las cantidades están expresadas en las unidades del SI.

4.5. Análisis de la velocidad de dos puntos de un sólido

Las velocidades, ${\vec {v}}^{A}$ y ${\vec {v}}^{B}$, de sendos puntos, A y B, de un sólido rígido respecto a un sistema de referencia fijo OXYZ han sido medidas en tres experimentos distintos. En todos ellos, los puntos A y B ocupaban idénticas posiciones respecto al triedro OXYZ, definidas por las coordenadas A(1,0,0) y B(0,1,0), respectivamente. Las velocidades medidas en los tres experimentos vienen dadas (en la base de OXYZ) por los siguientes pares de vectores:

• (a) $\,\,{\vec {v}}^{A}=v\,({\vec {\imath }}-{\vec {\jmath }})\,$; $\,\,{\vec {v}}^{B}=v\,({\vec {\imath }}-{\vec {\jmath }})$.
• (b) $\,\,{\vec {v}}^{A}=v\,({\vec {\imath }}+{\vec {\jmath }})\,$; $\,\,{\vec {v}}^{B}=v\,({\vec {\imath }}-{\vec {\jmath }})$.
• (c) $\,\,{\vec {v}}^{A}={\sqrt {2}}\,v{\vec {\imath }}\,$; $\,\,{\vec {v}}^{B}={\sqrt {2}}\,v{\vec {\imath }}$.

Si se sabe que cada una de las situaciones medidas corresponde a uno de los casos siguientes:

1. Se ha producido un error en las medidas.
2. La velocidad de deslizamiento es $v\,$.
3. El eje instantáneo de rotación y mínimo deslizamiento pasa por $A$ y $B$.

establezca razonadamente la relación de correspondencia entre los experimentos y los diferentes casos posibles.

4.6. Identificación de posibles movimientos rígidos

En un hipotético sólido rígido, consideramos los puntos

${\overrightarrow {OA}}={\vec {\imath }}\qquad {\overrightarrow {OB}}={\vec {\jmath }}\qquad {\overrightarrow {OC}}={\vec {k}}$

y analizamos los casos correspondientes a las siguientes velocidades para los tres puntos:

Caso	${\vec {v}}^{A}$	${\vec {v}}^{B}$	${\vec {v}}^{C}$
I	$2{\vec {\imath }}+2{\vec {\jmath }}+4{\vec {k}}$	$2{\vec {\imath }}+2{\vec {\jmath }}+4{\vec {k}}$	$2{\vec {k}}$
II	$2{\vec {\imath }}+{\vec {\jmath }}+2{\vec {k}}$	$3{\vec {\imath }}+2{\vec {\jmath }}$	$2{\vec {\imath }}+4{\vec {\jmath }}+2{\vec {k}}$
III	$2{\vec {\imath }}+2{\vec {\jmath }}+2{\vec {k}}$	$2{\vec {\imath }}+2{\vec {\jmath }}+2{\vec {k}}$	$2{\vec {\imath }}+2{\vec {\jmath }}+2{\vec {k}}$
IV	$2{\vec {\imath }}+3{\vec {\jmath }}$	${\vec {\imath }}+2{\vec {\jmath }}-{\vec {k}}$	$4{\vec {\imath }}+4{\vec {\jmath }}+2{\vec {k}}$
V	$2{\vec {\imath }}+{\vec {k}}$	$4{\vec {\imath }}+2{\vec {\jmath }}+3{\vec {k}}$	$3{\vec {\imath }}+{\vec {\jmath }}+2{\vec {k}}$
VI	$2{\vec {\imath }}+{\vec {\jmath }}+2{\vec {k}}$	$3{\vec {\imath }}+2{\vec {\jmath }}+2{\vec {k}}$	$-{\vec {\imath }}+{\vec {\jmath }}+2{\vec {k}}$

Todas las cantidades están expresadas en las unidades del SI.

Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.

4.7. Ejemplo de movimiento de precesión

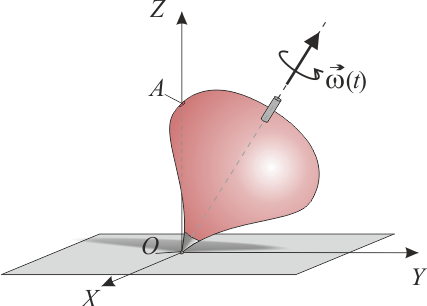
El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular

${\vec {v}}^{\,O}(t)={\vec {0}}\,\,;\qquad \qquad {\vec {\omega }}(t)=3\cos(t){\vec {\imath }}+3\,\mathrm {sen} (t){\vec {\jmath }}+4{\vec {k}}$

Consideremos el punto ${\overrightarrow {OA}}={\vec {k}}$

1. Determine la velocidad de este punto en cada instante.
2. Determine la aceleración de A en todo instante.
3. Halle, para cada instante, las componentes intrínsecas de la aceleración y el radio de curvatura en el mismo punto.

Todas las cantidades están expresadas en las unidades del SI.

4.8. Rodadura permanente de un disco

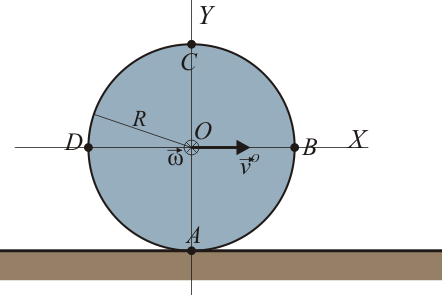
La rodadura permanente de un disco de radio $R$ sobre una superficie horizontal puede describirse mediante el campo de velocidades

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}\,\,;\qquad {\vec {v}}^{O}=v_{0}{\vec {\imath }}\,\,;\qquad {\vec {\omega }}=-{\frac {v_{0}}{R}}{\vec {k}}$

donde la superficie horizontal se encuentra en $y=-R$.

1. Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco.
2. Suponiendo $v_{0}=\mathrm {cte} \,$, calcule la aceleración de dichos puntos para el mismo instante.

4.9. Cálculo de una aceleración (Ex.Dic/11)

Un sólido se mueve respecto a un sistema de referencia fijo de forma que en todo instante la velocidad de la partícula del sólido que se encuentra en el origen del sistema de referencia ($O(0,0,0)\,$) vale ${\vec {v}}_{O}={\vec {\imath }}+{\vec {\jmath }}\,$, siendo la velocidad angular del sólido constante e igual a ${\vec {\omega }}=-2\,{\vec {\imath }}+2\,{\vec {\jmath }}-{\vec {k}}\,$ (todas las unidades en el SI).

1. ¿Qué tipo de movimiento realiza el sólido?
2. ¿Cuánto vale la aceleración de la partícula del sólido situada en el origen $O\,$?

No Boletín - Campo de aceleraciones de una traslación instantánea (Ex.Ene/15)

¿Cómo es necesariamente el campo de aceleraciones de un sólido rígido que está realizando una traslación instantánea?

(NOTA: sólo una de las cuatro opciones es correcta)

$\mathrm {(a)} \,\,\,\,\mathrm {Equiproyectivo} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(b)} \,\,\,\,\mathrm {Uniforme} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(c)} \,\,\,\,\mathrm {No} \,\,\mathrm {uniforme} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(d)} \,\,\,\,\mathrm {Nulo}$

No Boletín - Cuestión sobre EIRMD (Ex.Ene/12)

Dos puntos de un sólido rígido con movimiento helicoidal instantáneo (MHI) tienen las siguientes posiciones y velocidades:

$A(1,1,0)\,\mathrm {m} \,\,\,\,\longrightarrow \,\,\,\,{\vec {v}}_{A}=(3\,{\vec {\imath }}+2\,{\vec {\jmath }}\,)\,\mathrm {m/s} \,;\,\,\,\,\,\,\,\,\,\,B(-5,-3,0)\,\mathrm {m} \,\,\,\,\longrightarrow \,\,\,\,{\vec {v}}_{B}=(3\,{\vec {\imath }}+2\,{\vec {\jmath }}\,)\,\mathrm {m/s}$

¿Dónde se halla el eje instantáneo de rotación y mínimo deslizamiento (EIRMD)?

No Boletín - Cuestión sobre EIRMD II (Ex.Sep/14)

El campo de velocidades de un sólido rígido en movimiento helicoidal instantáneo (respecto a un triedro OXYZ de referencia) está definido mediante la siguiente reducción cinemática:

${\vec {\omega }}=(\,2\,{\vec {\imath }}\,-\,{\vec {\jmath }}\,)\,\mathrm {rad} /\mathrm {s} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,A(2,2,2)\,\mathrm {m} \,\longrightarrow \,{\vec {v}}_{A}=(\,5\,{\vec {\imath }}\,-\,15\,{\vec {\jmath }}\,+\,5\,{\vec {k}}\,)\,\mathrm {m} /\mathrm {s}$

¿Por cuál de los siguientes puntos pasa el eje instantáneo de rotación y mínimo deslizamiento?

$\mathrm {(a)} \,\,\,\,I\mathrm {(1,0,-3)} \,\mathrm {m} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(b)} \,\,\,\,I\mathrm {(2,-1,-3)} \,{\mbox{m}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(c)} \,\,\,\,I\mathrm {(-1,-2,-5)} \,{\mbox{m}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(d)} \,\,\,\,I\mathrm {(2,2,2)} \,{\mbox{m}}$

No Boletín - Cuestión sobre EIRMD III (Ex.Ene/16)

Un sólido rígido realiza un movimiento helicoidal instantáneo respecto a un triedro de referencia $OXYZ\,$, estando definido su campo de velocidades mediante la siguiente reducción cinemática en el origen de coordenadas $\,O\,$:

${\vec {\omega }}=(\,2\,{\vec {\imath }}+{\vec {\jmath }}-2\,{\vec {k}}\,)\,\mathrm {rad} /\mathrm {s} \,\,;\,\,\,\,\,\,{\vec {v}}_{O}=(\,2\,{\vec {\imath }}-7\,{\vec {k}}\,)\,\mathrm {m} /\mathrm {s}$

1. Calcule la velocidad de deslizamiento del sólido rígido (segundo invariante).
2. ¿Por cuál de los siguientes puntos pasa el eje instantáneo de rotación y mínimo deslizamiento?

$\,\,\,\,\,\,\,\,\,\,\mathrm {(a)} \,\,\,\,P\mathrm {(1,2,0)} \,\mathrm {m} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(b)} \,\,\,\,P\mathrm {(0,0,0)} \,{\mbox{m}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(c)} \,\,\,\,P\mathrm {(-1,1,0)} \,{\mbox{m}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm {(d)} \,\,\,\,P\mathrm {(2,1,-2)} \,{\mbox{m}}$

No Boletín - Cuestión sobre MHI (Ex.Ene/13)

Dado un sólido rígido con movimiento helicoidal instantáneo (MHI), se han medido las velocidades de dos puntos del mismo:

$A(0,0,0)\,\mathrm {m} \,\,\,\,\longrightarrow \,\,\,\,{\vec {v}}_{A}=({\vec {\imath }}+{\vec {\jmath }}\,)\,\mathrm {m/s} \,;\,\,\,\,\,\,\,\,\,\,B(1,1,1)\,\mathrm {m} \,\,\,\,\longrightarrow \,\,\,\,{\vec {v}}_{B}=({\vec {\imath }}+{\vec {\jmath }}\,)\,\mathrm {m/s}$

¿Cuál de las siguientes afirmaciones es correcta?

(a) Esas velocidades no son compatibles con un MHI.

(b) $A\,$ y $B\,$ pertenecen al eje instantáneo de rotación y mínimo deslizamiento (EIRMD).

(c) Esas velocidades no son compatibles con la rigidez.

(d) El valor absoluto de la velocidad de deslizamiento es $|v_{d}|=\displaystyle {\frac {2}{\sqrt {3}}}\,\mathrm {m/s} \,$.

Nota: Sólo una de las cuatro afirmaciones es correcta.

No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)

Las posiciones y velocidades instantáneas de tres puntos de un sólido rígido vienen dadas por:

Punto	${\vec {r}}$ (m)	${\vec {v}}$ (m/s)
A	${\vec {\imath }}-{\vec {\jmath }}+{\vec {k}}$	$-{\vec {\imath }}-2\,{\vec {\jmath }}-4\,{\vec {k}}$
B	$2\,{\vec {\imath }}+{\vec {\jmath }}$	$-{\vec {\jmath }}-{\vec {k}}$
C	${\vec {0}}$	$-{\vec {\imath }}+{\vec {\jmath }}-{\vec {k}}$

¿Cuál de las siguientes afirmaciones es verdadera?

(a) Estos datos son incompatibles con la rigidez

(b) La velocidad de deslizamiento (segundo invariante) vale $v_{d}=-\displaystyle {\frac {2}{\sqrt {6}}}\,\,\mathrm {m/s} \,$

(c) La velocidad angular (primer invariante) vale ${\vec {\omega }}=(2\,{\vec {\imath }}-{\vec {\jmath }}-{\vec {k}}\,)\,\mathrm {rad/s} \,$

(d) El eje instantáneo de rotación pasa por el punto de coordenadas $(1,1,0)\,$

No Boletín - Detección de invariantes (Ex.Feb/14)

En el contexto de la cinemática del sólido rígido, se utiliza la palabra "invariante" en un sentido espacial (no temporal). Por eso, se denomina invariante a cualquier magnitud cuyo valor no varía de un punto a otro del sólido rígido.

¿Cuál de las siguientes magnitudes no es un invariante?

1) ${\vec {v}}_{P}\cdot {\vec {\omega }}\,$           2) ${\vec {\omega }}\,$            3) ${\vec {a}}_{P}\cdot {\vec {\alpha }}\,$            4) ${\vec {v}}_{P}\cdot {\vec {\alpha }}+{\vec {a}}_{P}\cdot {\vec {\omega }}\,$

No Boletín - Disco con centro acelerado rodando sin deslizar (Ex.Ene/13)

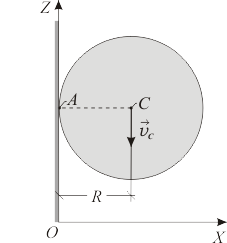
Un disco de radio $R\,$, contenido en todo instante en el plano $OXZ\,$, rueda sin deslizar sobre el eje $OZ\,$. El centro $C\,$ del disco avanza en el sentido negativo del eje $OZ\,$ (ver figura) con una celeridad linealmente creciente con el tiempo $|{\vec {v}}_{C}|=a\,t\,$ (donde $a\,$ es una constante positiva conocida). Para el instante $t\,$, al cual corresponde la posición del disco representada en la figura, se pregunta:

1. ¿Cuánto vale la velocidad angular instantánea ${\vec {\omega }}\,$ del disco?
2. ¿Y la aceleración instantánea ${\vec {a}}_{A}\,$ del punto del disco que se halla en contacto con el eje $OZ\,\,$?

No Boletín - Disco rotando alrededor de un punto fijo de su perímetro (Ex.Sep/12)

Un disco de radio $R\,$, contenido en todo instante en el plano OYZ, rota en sentido antihorario alrededor de un punto fijo de su perímetro que coincide con el origen de coordenadas $O\,$. Sea $A\,$ el punto del perímetro discal diametralmente opuesto a $O\,$, y sea $\theta \,$ el ángulo que forma el diámetro OA con el eje OY. Se sabe que el punto $A\,$ del disco está realizando un movimiento uniforme y que el módulo de su aceleración vale $8\,\Omega ^{2}R\,$.

1. Determine la ley horaria para el ángulo $\theta \,$.
2. Calcule la velocidad instantánea del centro $C\,$ del disco en el instante en que $\,\theta =\pi /6\,\mathrm {rad}$.

No Boletín - Dos partículas con distancia mutua constante (Ex.Jun/13)

Las partículas $A\,$ y $B\,$ se mueven en el plano $OXY\,$ de tal modo que su distancia mutua permanece constante a lo largo del tiempo:

$|{\overrightarrow {BA}}(t)|\equiv |{\vec {r}}_{A}(t)-{\vec {r}}_{B}(t)|=\mathrm {cte}$

Además, $B\,$ persigue a $A\,$, es decir, el vector velocidad ${\vec {v}}_{B}$ tiene siempre la misma dirección que la recta imaginaria que pasa por $B\,$ y $A\,$. En cierto instante, las posiciones de ambas partículas son $A(4,0)\,\mathrm {m} \,$ y $B(0,3)\,\mathrm {m} \,$, y la velocidad de $A\,$ es ${\vec {v}}_{A}=20\,{\vec {\imath }}\,\,\mathrm {m/s} \,$ (ver figura).

¿Cuánto vale la celeridad de $B\,$ en dicho instante?

No Boletín - Dos partículas con distancia mutua constante II (Ex.Feb/17)

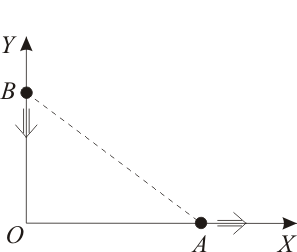
Las partículas $A\,$ y $B\,$ se mueven a lo largo de los ejes $OX\,$ y $OY\,$, respectivamente, en los sentidos de avance que se indican en la figura, y de tal modo que su distancia mutua permanece constante en el tiempo:

$|{\overrightarrow {BA}}\,(t)|\equiv |{\vec {r}}_{A}(t)-{\vec {r}}_{B}(t)|=\mathrm {cte}$

En cierto instante, las celeridades de las partículas son $v_{A}=6\,\mathrm {m} \mathrm {/} \mathrm {s} \,$ y $v_{B}=9\,\mathrm {m} \mathrm {/} \mathrm {s} \,$, respectivamente, y la posición de la primera partícula es $A(6,0,0)\,\mathrm {m} \,$.

¿Cuál es la posición de la segunda partícula en dicho instante?

No Boletín - Eje central (Ex.Ene/19)

Sea un sólido rígido en movimiento instantáneo. La velocidad angular es ${\vec {\omega }}=(2\,{\vec {\imath }}-{\vec {\jmath }}+2\,{\vec {k}}\,)\,\,\mathrm {rad/s} \,$, la velocidad de deslizamiento (segundo invariante) es $v_{d}=-2\,\,\mathrm {m/s} \,$, y la velocidad del punto $A(2,1,2)\,\,\mathrm {m} \,$ es ${\vec {v}}_{A}=(v_{x}\,{\vec {\imath }}\,-2\,{\vec {\jmath }}\,+4\,{\vec {k}}\,)\,\,\mathrm {m/s} \,$.

1. ¿Cuánto vale la componente $x\,$ de la velocidad del punto $A\,$?
2. ¿Cuál es el valor (en $\mathrm {m/s} \,$) de la velocidad de los puntos del eje central del campo de velocidades?
3. ¿Cuál de los siguientes puntos pertenece a dicho eje central?

$\,\,\,\,\,\,\,\,\,\,B\left(0,-\displaystyle {\frac {2}{3}},-\displaystyle {\frac {4}{3}}\right)\,\mathrm {m} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C\left(\displaystyle {\frac {8}{3}},0,-\displaystyle {\frac {4}{3}}\right)\,\mathrm {m} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D\left(0,-\displaystyle {\frac {8}{3}},-\displaystyle {\frac {4}{3}}\right)\,\mathrm {m} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,E\left(\displaystyle {\frac {4}{3}},\displaystyle {\frac {4}{3}},0\right)\,\mathrm {m}$

No Boletín - Ejemplo de campo de velocidades de un sólido II (Ex.Ene/20)

Sea un sólido rígido en movimiento respecto a un triedro cartesiano OXYZ. En cierto instante, el campo de velocidades del sólido tiene la siguiente expresión (unidades del SI):

${\vec {v}}=(2-y)\,{\vec {\imath }}+(1+x+z)\,{\vec {\jmath }}-y\,{\vec {k}}$

donde $(x,y,z)\,$ son las coordenadas cartesianas de cada punto del sólido.

1. Verifique la equiproyectividad del campo de velocidades.
2. ¿Cuál es la velocidad angular instantánea del sólido rígido?

No Boletín - Identificación de movimiento a partir de dos velocidades (Ex.Sep/15)

Se conocen las velocidades de dos puntos de un sólido rígido en un instante dado:

$A\,(1,-1,0)\,\mathrm {m} \,\longrightarrow \,{\vec {v}}_{A}=(-{\vec {\imath }}\,+\,{\vec {\jmath }}\,-\,{\vec {k}}\,)\,\mathrm {m} \mathrm {/s} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B\,(2,1,1)\,\mathrm {m} \,\longrightarrow \,{\vec {v}}_{B}=(-{\vec {\imath }}\,+\,{\vec {\jmath }}\,-\,{\vec {k}}\,)\,\mathrm {m} \mathrm {/s}$

¿Qué sabemos con certeza de este movimiento instantáneo? (NOTA: hay que elegir sólo una de las cuatro siguientes afirmaciones).

(a) Puede ser traslación o helicoidal.

(b) Es traslación.

(c) Puede ser traslación o rotación.

(d) Es helicoidal.

No Boletín - Identificación de movimiento a partir de reducción cinemática (Ex.Ene/15)

Sea un sólido rígido en movimiento respecto a un triedro de referencia OXYZ. En un instante dado, se conoce el vector velocidad angular del sólido y la velocidad de su punto $O(0,0,0)\,$:

$\,\,\,\,\,\,\,\,\,\,\,{\vec {\omega }}=(-2\,{\vec {\imath }}\,+\,{\vec {\jmath }}\,+\,2\,{\vec {k}}\,)\,\,\mathrm {rad} /\mathrm {s} \,\,\,;\,\,\,\,\,\,\,\,\,\,\,{\vec {v}}_{O}=(\,2\,{\vec {\imath }}\,-\,2\,{\vec {\jmath }}\,+\,{\vec {k}}\,)\,\,\mathrm {m} /\mathrm {s}$

1. ¿Cuál es la velocidad de su punto $A(-2,1,2)\,\,\mathrm {m} \,\,$?
2. ¿Qué tipo de movimiento instantáneo es?

No Boletín - Tres velocidades con tres parámetros n, p y q (Ex.Ene/12)

En un instante dado, las posiciones y velocidades de tres puntos de un sólido rígido respecto a un triedro cartesiano OXYZ son las siguientes:

Punto	${\vec {r}}$ (m)	${\vec {v}}$ (m/s)
A	${\vec {\imath }}$	${\vec {\imath }}+(1+n)\,{\vec {\jmath }}+(1-p)\,{\vec {k}}$
B	${\vec {\jmath }}$	$(1-n)\,{\vec {\imath }}+{\vec {\jmath }}+(1+q)\,{\vec {k}}$
C	${\vec {k}}$	$(1+p)\,{\vec {\imath }}+(1-q)\,{\vec {\jmath }}+{\vec {k}}$

1. Verifique que estos datos son compatibles con la rigidez del sólido independientemente de los valores de $n\,$, $p\,$ y $q\,$.
2. Determine la velocidad instantánea del punto $O\,$ del sólido que se halla en el origen de coordenadas.
3. ¿Para qué valores particulares de $n\,$, $p\,$ y $q\,$ estaría el sólido realizando una traslación instantánea?
4. Halle el vector velocidad angular y la velocidad de deslizamiento del sólido en función de $n\,$, $p\,$ y $q\,$.
5. Determine qué condiciones matemáticas deberían cumplir $n\,$, $p\,$ y $q\,$ para que el sólido estuviera realizando un movimiento helicoidal instantáneo cuyo EIRMD pasara por el origen de coordenadas. ¿Qué valor tendría en tal caso la velocidad de deslizamiento?

No Boletín - Velocidad angular y eje central (Ex.Ene/13)

En un instante dado, las posiciones y velocidades de tres puntos ($A\,$, $B\,$ y $C\,$) de un sólido rígido son las siguientes:

$A(0,0,0)\,\mathrm {m} \,\rightarrow \,{\vec {v}}_{A}=10\,{\vec {k}}\,\,\mathrm {m/s} \,\,;\,\,\,\,\,B(6,0,0)\,\mathrm {m} \,\rightarrow \,{\vec {v}}_{B}=10\,{\vec {k}}\,\,\mathrm {m/s} \,\,;\,\,\,\,\,C(0,6,0)\,\mathrm {m} \,\rightarrow \,{\vec {v}}_{C}=-10\,{\vec {k}}\,\,\mathrm {m/s}$

1. ¿Cuánto vale la velocidad angular instantánea del sólido rígido?
2. ¿Cuál de las siguientes afirmaciones (sólo una) es cumplida por el eje central del campo de velocidades del sólido rígido en dicho instante? (a) Es paralelo al eje $OZ\,$ y pasa por el punto $I(0,3,0)\,\mathrm {m} \,$. (b) Es paralelo al eje $OX\,$ y pasa por el punto $I(6,3,0)\,\mathrm {m} \,$. (c) No verifica lo dicho en ninguna de las otras tres respuestas. (d) Pasa por los puntos $A\,$ y $B\,$.