Problemas de herramientas matemáticas (GIOI)

Arco capaz

Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores ${\overrightarrow {AP}}$ y ${\overrightarrow {BP}}$ son ortogonales.

Inversamente, sean A, B y P tres puntos tales que ${\overrightarrow {AP}}\perp {\overrightarrow {BP}}$. Pruebe que el centro de la circunferencia que pasa por A, B y P se encuentra en el punto medio del segmento AB.

Solución

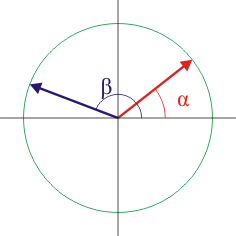
Coseno y seno de una diferencia

A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.

Solución

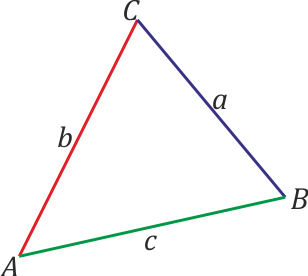
Teoremas del seno y del coseno

Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno

$c^{2}=a^{2}+b^{2}-2ab\,\mathrm {cos} (C)$

y del seno

${\frac {\mathrm {sen} \,A}{a}}={\frac {\mathrm {sen} \,B}{b}}={\frac {\mathrm {sen} \,C}{c}}$

en un triángulo de lados $a$, $b$ y $c$, y ángulos opuestos $A$, $B$ y $C$.

Solución

Construcción de una base

Dados los vectores

${\vec {v}}={\vec {\imath }}+2{\vec {\jmath }}+2{\vec {k}}\qquad \qquad {\vec {a}}=6{\vec {\imath }}+9{\vec {\jmath }}+6{\vec {k}}$

Construya una base ortonormal dextrógira $\{{\vec {T}},{\vec {N}},{\vec {B}}\}$, tal que

1. El primer vector, ${\vec {T}}$, vaya en la dirección y sentido de ${\vec {v}}$
2. El segundo, ${\vec {N}}$, esté contenido en el plano definido por ${\vec {v}}$ y ${\vec {a}}$ y apunte hacia el mismo semiplano (respecto de ${\vec {v}}$) que el vector ${\vec {a}}$.
3. El tercero, ${\vec {B}}$, sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
4. Supongamos un vector que en la base canónica se escribe

${\vec {F}}=-12{\vec {k}}$

¿Cuál es su expresión en la base $\left\{{\vec {T}},{\vec {N}},{\vec {B}}\right\}$

Solución

Ejemplo de operaciones con dos vectores

Dados los vectores

${\vec {v}}=2.0{\vec {\imath }}+3.5{\vec {\jmath }}-4.2{\vec {k}}\qquad \qquad {\vec {a}}=4.5{\vec {\imath }}-2.2{\vec {\jmath }}+1.5{\vec {k}}$

1. ¿Qué ángulo forman estos dos vectores?
2. ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
3. Escriba ${\vec {a}}$ como suma de dos vectores, uno paralelo a ${\vec {v}}$ y otro ortogonal a él.

Solución

Ángulo entre diagonales

Calcule el ángulo que forman dos diagonales de un cubo.

Solución

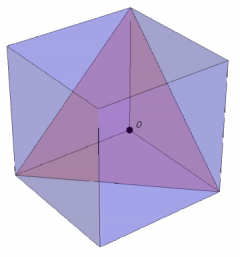
Distancia de un vértice a un plano

Sea un cubo de arista b siendo O uno de sus vértices. ¿Cuánto mide la distancia de O al plano definido por sus tres vértices contiguos?

Solución

Determinación de un vector a partir de sus proyecciones

Se tiene un vector conocido, no nulo, ${\vec {A}}$ y uno que se desea determinar, ${\vec {X}}$. Se dan como datos su producto escalar y su producto vectorial por ${\vec {A}}$

${\vec {A}}\cdot {\vec {X}}=k\qquad {\vec {A}}\times {\vec {X}}={\vec {C}}$

Determine el valor de ${\vec {X}}$. ¿Es suficiente una sola de las dos ecuaciones para hallarlo?

Solución

Cálculo de las componentes de un vector

De una fuerza ${\vec {F}}_{1}$ se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?

Si a esta fuerza se le suma otra ${\vec {F}}_{2}=(-10{\vec {\imath }}-10{\vec {\jmath }})\,\mathrm {N}$, ¿qué ángulo forma la resultante con los ejes coordenados?

Solución

Base vectorial girada

Considere la terna de vectores

${\vec {u}}_{1}=\cos(\theta ){\vec {\imath }}+\mathrm {sen} (\theta ){\vec {\jmath }}\qquad {\vec {u}}_{2}=-\mathrm {sen} (\theta ){\vec {\imath }}+\cos(\theta ){\vec {\jmath }}\qquad {\vec {u}}_{3}={\vec {k}}$

1. Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
2. Halle la transformación inversa, es decir, exprese $\{{\vec {\imath }},{\vec {\jmath }},{\vec {k}}\}$ como combinación de $\{{\vec {u}}_{1},{\vec {u}}_{2},{\vec {u}}_{3}\}$.
3. Para el caso particular en que $\mathrm {tg} (\theta )=3/4$, particularice las ecuaciones de transformación y exprese el vector ${\vec {F}}=10{\vec {\imath }}-15{\vec {\jmath }}+3{\vec {k}}$ en la nueva base.

Solución

Desplazamiento de un momento

El momento del vector ${\vec {v}}=2{\vec {\imath }}-2{\vec {\jmath }}+{\vec {k}}$ respecto al origen de coordenadas vale ${\vec {M}}_{O}=8{\vec {\imath }}+5{\vec {\jmath }}-6{\vec {k}}$.

1. ¿Cuánto vale su momento respecto al punto A(-1,4,1)?
2. ¿Cuál es la ecuación de la recta soporte de ${\vec {v}}$?

Solución