Base vectorial girada

Enunciado

Considere la terna de vectores

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1 = \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \qquad \vec{u}_2 = -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \qquad \vec{u}_3 = \vec{k} }

1. Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
2. Halle la transformación inversa, es decir, exprese Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\imath},\vec{\jmath},\vec{k}\}} como combinación de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_1,\vec{u}_2,\vec{u}_3\}} .
3. Para el caso particular en que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(\theta) = 3/4} , particularice las ecuaciones de transformación y exprese el vector Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=10\vec{\imath}-15\vec{\jmath}+3\vec{k}} en la nueva base.

Base ortonormal dextrógira

Base ortonormal

Para demostrar que se tra de una base ortonormal hay que probar que son unitarios y ortogonales entre sí, es decir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_i\cdot\vec{u}_k=\begin{cases}1 & i = k \\ 0 & i\neq k\end{cases}}

Calculamos entonces los productos escalares:

• De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1} consigo mismo

${\vec {u}}_{1}\cdot {\vec {u}}_{1}=\cos ^{2}(\theta )+\mathrm {sen} ^{2}(\theta )=1$

• De ${\vec {u}}_{1}$ con ${\vec {u}}_{2}$ (y viceversa, por la conmutatividad)

${\vec {u}}_{1}\cdot {\vec {u}}_{2}={\vec {u}}_{2}\cdot {\vec {u}}_{1}=\cos(\theta )(-\mathrm {sen} (\theta ))+\mathrm {sen} (\theta )\cos(\theta )=0$

• De ${\vec {u}}_{1}$ con ${\vec {u}}_{3}$ (y viceversa). Es fácil ver que son ortogonales ya que ${\vec {u}}_{1}$ no tiene componente en ${\vec {k}}$

${\vec {u}}_{1}\cdot {\vec {u}}_{3}={\vec {u}}_{3}\cdot {\vec {u}}_{1}=(\cos(\theta ){\vec {\imath }}+\mathrm {sen} (\theta ){\vec {\jmath }})\cdot {\vec {k}}=\cos(\theta )\overbrace {{\vec {\imath }}\cdot {\vec {k}}} ^{=0}+\mathrm {sen} (\theta )\overbrace {{\vec {\jmath }}\cdot {\vec {k}}} ^{=0}=0$

• De ${\vec {u}}_{2}$ consigo mismo

${\vec {u}}_{2}\cdot {\vec {u}}_{2}=(-\mathrm {sen} (\theta ))^{2}+\cos ^{2}(\theta )=1$

• De ${\vec {u}}_{2}$ con ${\vec {u}}_{3}$ (y viceversa). Se anula el producto escalar por la misma razón que el de ${\vec {u}}_{1}$ con ${\vec {u}}_{3}$

${\vec {u}}_{2}\cdot {\vec {u}}_{3}={\vec {u}}_{3}\cdot {\vec {u}}_{1}=(-\mathrm {sen} (\theta ){\vec {\imath }}+\cos(\theta ){\vec {\jmath }})\cdot {\vec {k}}=-\mathrm {sen} (\theta )\overbrace {{\vec {\imath }}\cdot {\vec {k}}} ^{=0}+\cos(\theta )\overbrace {{\vec {\jmath }}\cdot {\vec {k}}} ^{=0}=0$

• De ${\vec {u}}_{3}$ consigo mismo

${\vec {u}}_{3}\cdot {\vec {u}}_{3}={\vec {k}}\cdot {\vec {k}}=1$

Por tanto, hemos demostrado que la relación anterior para los productos escalares se cumple y la base es ortonormal.

Base dextrogira

Para demostrar que se trata de una base dextrógira hemos de probar que se cumple la regla de la mano derecha, es decir, que

${\vec {u}}_{1}\times {\vec {u}}_{2}={\vec {u}}_{3}\qquad \qquad {\vec {u}}_{2}\times {\vec {u}}_{3}={\vec {u}}_{1}\qquad \qquad {\vec {u}}_{3}\times {\vec {u}}_{1}={\vec {u}}_{2}$

Probamos la primera de las igualdades

${\vec {u}}_{1}\times {\vec {u}}_{2}=\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\\cos(\theta )&\mathrm {sen} (\theta )&0\\-\mathrm {sen} (\theta )&\cos(\theta )&0\end{matrix}}\right|=(\cos ^{2}(\theta )+\mathrm {sen} ^{2}(\theta )){\vec {k}}={\vec {k}}$

De la misma manera se demuestran las otras dos igualdades. Una forma alternativa de demostrarlas es observar que

${\vec {u}}_{2}\times {\vec {u}}_{3}={\vec {u}}_{2}\times ({\vec {u}}_{1}\times {\vec {u}}_{2})$

Aplicamos las propiedades del doble producto vectorial

${\vec {u}}_{2}\times {\vec {u}}_{3}=\overbrace {({\vec {u}}_{2}\cdot {\vec {u}}_{2})} ^{=1}{\vec {u}}_{1}-\overbrace {({\vec {u}}_{2}\cdot {\vec {u}}_{1})} ^{=0}{\vec {u}}_{2}={\vec {u}}_{1}$

y de la misma manera se obtiene la tercera

${\vec {u}}_{3}\times {\vec {u}}_{1}={\vec {u}}_{2}$

por lo que la base es ortonormal y dextrógira.

Esta base supone una rotación de un ángulo $\theta$ alrededor del eje OZ.

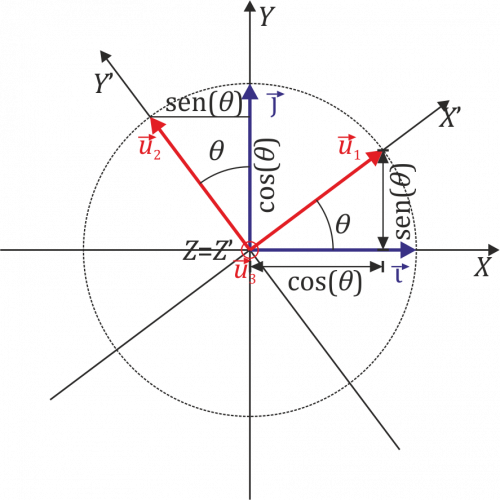
Transformación inversa

La transformación inversa consiste en escribir la base canónica $\{{\vec {\imath }},{\vec {\jmath }},{\vec {k}}\}$ como combinación lineal de la base $\{{\vec {u}}_{1},{\vec {u}}_{2},{\vec {u}}_{3}\}$, es decir, escribir ${\vec {\imath }}$ en la forma

${\vec {\imath }}=(\ldots ){\vec {u}}_{1}+(\ldots ){\vec {u}}_{2}+(\ldots ){\vec {u}}_{3}$

para ello, aplicamos que las componentes de un vector en una base ortonormal se obtienen proyectando sobre cada vector de esa base

${\vec {F}}=F_{1}{\vec {u}}_{1}+F_{2}{\vec {u}}_{2}+F_{3}{\vec {u}}_{3}\qquad \Rightarrow \qquad F_{k}={\vec {F}}\cdot {\vec {u}}_{k}$

y que el producto escalar es independiente de la base que se emplee para calcularlo. En particular podemos emplear la propia base canónica. En ese caso las componentes de ${\vec {\imath }}$ serán

${\begin{array}{rcl}i_{1}={\vec {\imath }}\cdot {\vec {u}}_{1}&=&{\vec {\imath }}\cdot (\cos(\theta ){\vec {\imath }}+\mathrm {sen} (\theta ){\vec {\jmath }})=\cos(\theta )\\i_{1}={\vec {\imath }}\cdot {\vec {u}}_{2}&=&{\vec {\imath }}\cdot (-\mathrm {sen} (\theta ){\vec {\imath }}+\mathrm {cos} (\theta ){\vec {\jmath }})=-\mathrm {sen} (\theta )\\i_{1}={\vec {\imath }}\cdot {\vec {u}}_{3}&=&{\vec {\imath }}\cdot {\vec {k}}=0\end{array}}$

y por tanto

${\vec {\imath }}=\cos(\theta ){\vec {u}}_{1}-\mathrm {sen} (\theta ){\vec {u}}_{2}$

De la misma manera obtenemos

${\vec {\jmath }}=\mathrm {sen} (\theta ){\vec {u}}_{1}+\mathrm {cos} (\theta ){\vec {u}}_{2}$

y, trivialmente,

${\vec {k}}={\vec {u}}_{3}$

Gráficamente, lo que hacemos ahora es proyectar ortogonalmente la antigua base sobre la nueva.

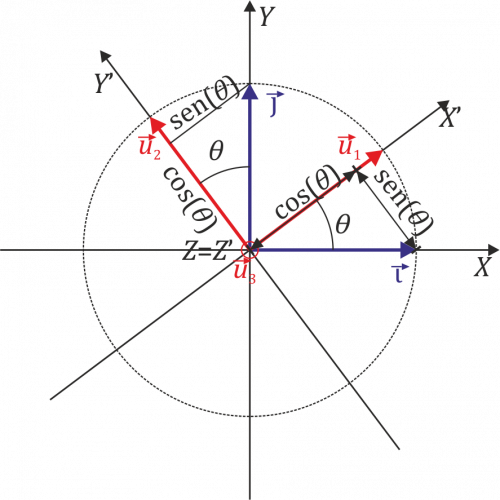
Caso particular

En el caso particular $\mathrm {tg} (\theta )=0.75=3/4$ el seno y el coseno valen

$\cos(\theta )={\frac {4}{\sqrt {4^{2}+3^{2}}}}={\frac {4}{5}}=0.8\qquad \qquad \mathrm {sen} (\theta )={\frac {3}{\sqrt {4^{2}+3^{2}}}}={\frac {3}{5}}=0.6$

con lo que la relación entre las bases se particulariza a

${\vec {u}}_{1}={\frac {4}{5}}{\vec {\imath }}+{\frac {3}{5}}{\vec {\jmath }}\qquad {\vec {u}}_{2}=-{\frac {3}{5}}{\vec {\imath }}+{\frac {4}{5}}{\vec {\jmath }}\qquad {\vec {u}}_{3}={\vec {k}}$

Para hallar las componentes de

${\vec {F}}=10{\vec {\imath }}-15{\vec {\jmath }}+3{\vec {k}}$

aplicamos de nuevo que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=F_1\vec{u}_1+F_2\vec{u}_2+F_3\vec{u}_3\qquad\Rightarrow\qquad F_k=\vec{F}\cdot\vec{u}_k}

lo que nos da

${\begin{array}{rcl}F_{1}={\vec {F}}\cdot {\vec {u}}_{1}&=&\left(10{\vec {\imath }}-15{\vec {\jmath }}+3{\vec {k}}\right)\cdot \left({\dfrac {4}{5}}{\vec {\imath }}+{\dfrac {3}{5}}{\vec {\jmath }}\right)={\dfrac {10\times 4-15\times 3}{5}}=-1\\&&\\F_{2}={\vec {F}}\cdot {\vec {u}}_{2}&=&\left(10{\vec {\imath }}-15{\vec {\jmath }}+3{\vec {k}}\right)\cdot \left(-{\dfrac {3}{5}}{\vec {\imath }}+{\dfrac {4}{5}}{\vec {\jmath }}\right)={\dfrac {-10\times 3-15\times 4}{5}}=-18\\&&\\F_{1}={\vec {F}}\cdot {\vec {u}}_{3}&=&\left(10{\vec {\imath }}-15{\vec {\jmath }}+3{\vec {k}}\right)\cdot \left({\vec {k}}\right)=3\end{array}}$

y por tanto la expresión de ${\vec {F}}$ en esta base es

${\vec {F}}=-{\vec {u}}_{1}-18{\vec {u}}_{2}+3{\vec {u}}_{3}$

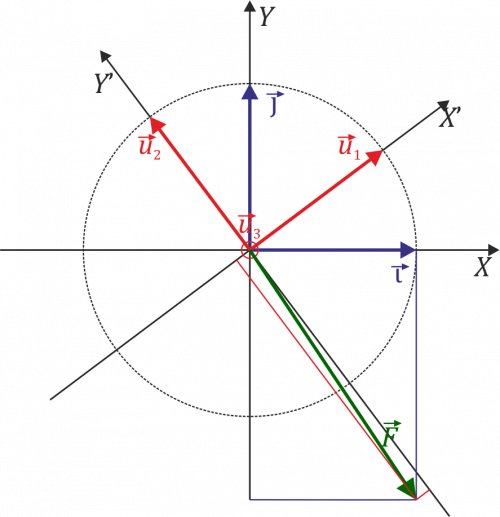
Hay que destacar que aunque las componentes cambien, el vector en sí no se ha visto modificado.

Podemos ver que el módulo del vector no se ve afectado porque usemos una base u otra

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sqrt{10^2+15^2+3^2} = \sqrt{334}\qquad\qquad\sqrt{1^2+18^2+3^2}=\sqrt{334}}