Distancia de un vértice a un plano

Enunciado

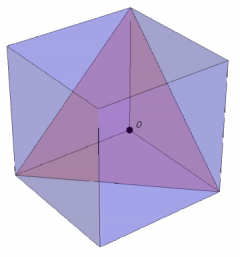
Sea un cubo de arista b siendo O uno de sus vértices. ¿Cuánto mide la distancia de O al plano definido por sus tres vértices contiguos?

Solución

La distancia de un punto O a un plano es

$d={\frac {{\overrightarrow {OA}}\cdot {\vec {n}}}{|{\vec {n}}|}}$

Siendo ${\vec {n}}$ un vector normal al plano. Si lo que conocemos son tres puntos del plano, A, B y C, podemos hallar un vector normal mediante el producto vectorial de dos vectores tangentes

${\vec {n}}={\overrightarrow {AB}}\times {\overrightarrow {AC}}$

En este caso, los tres puntos del plano son

${\overrightarrow {OA}}=b{\vec {\imath }}\qquad \qquad {\overrightarrow {OB}}=b{\vec {\jmath }}\qquad \qquad {\overrightarrow {OC}}=b{\vec {k}}$

lo que nos da los vectores de posición relativa

${\overrightarrow {AB}}={\overrightarrow {OB}}-{\overrightarrow {OA}}=b\left(-{\vec {\imath }}+{\vec {\jmath }}\right)\qquad \qquad {\overrightarrow {AC}}={\overrightarrow {OC}}-{\overrightarrow {OA}}=b\left(-{\vec {\imath }}+{\vec {k}}\right)$

y el vector normal

${\vec {n}}={\overrightarrow {AB}}\times {\overrightarrow {AC}}=\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\-b&b&0\\-b&0&b\end{matrix}}\right|=b^{2}\left({\vec {\imath }}+{\vec {\jmath }}+{\vec {k}}\right)$

con módulo

$\left|{\vec {n}}\right|=b^{2}{\sqrt {3}}$

Por tanto la distancia buscada mide

$d={\frac {(b{\vec {\imath }})\cdot \left(b^{2}\left({\vec {\imath }}+{\vec {\jmath }}+{\vec {k}}\right)\right)}{b^{2}{\sqrt {3}}}}={\frac {b}{\sqrt {3}}}={\frac {b{\sqrt {3}}}{3}}$

Esta distancia no es la mitad de la diagonal cúbica, sino la tercera parte.