Teoremas del seno y del coseno (GIOI)

Enunciado

Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno

$c^{2}=a^{2}+b^{2}-2ab\,\mathrm {cos} (C)$

y del seno

${\frac {\mathrm {sen} \,A}{a}}={\frac {\mathrm {sen} \,B}{b}}={\frac {\mathrm {sen} \,C}{c}}$

en un triángulo de lados $a$, $b$ y $c$, y ángulos opuestos $A$, $B$ y $C$.

Teorema del coseno

Si consideramos los lados del triángulo como segmentos orientados,

${\vec {a}}={\overrightarrow {BC}}\qquad \qquad {\vec {b}}={\overrightarrow {CA}}\qquad \qquad {\vec {c}}={\overrightarrow {BA}}$

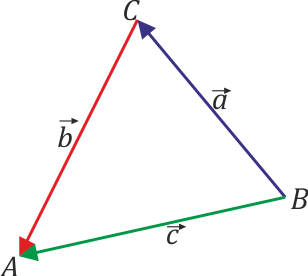
se verifica la ecuación vectorial

${\overrightarrow {BA}}={\overrightarrow {BC}}+{\overrightarrow {CA}}\qquad \Rightarrow \qquad {\vec {c}}={\vec {a}}+{\vec {b}}$

Si multiplicamos esta ecuación escalarmente por sí misma

$({\vec {a}}+{\vec {b}})\cdot ({\vec {a}}+{\vec {b}})={\vec {c}}\cdot {\vec {c}}=c^{2}$

Desarrollando el producto escalar

${\vec {a}}\cdot {\vec {a}}+2{\vec {a}}\cdot {\vec {b}}+{\vec {b}}\cdot {\vec {b}}=a^{2}+2ab\cos(\gamma )+b^{2}=c^{2}$

El ángulo $\gamma$ que forman los vectores ${\vec {a}}$ y${\vec {b}}$ no es igual a C, ya que para poder medir el ángulo que forman dos vectores deben tener un origen común. Trasladando el vector ${\vec {a}}$ vemos que

$\gamma =\pi -C\,$

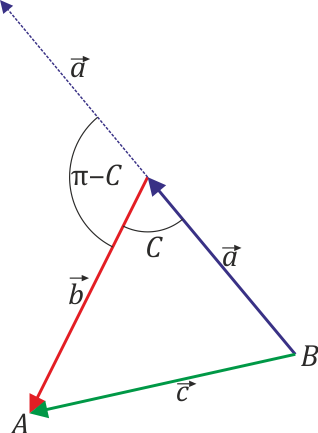
por lo que finalmente obtenemos

$a^{2}-2ab\,\cos(C)+b^{2}=c^{2}$

que es el teorema del coseno.

Expresiones análogas pueden obtenerse para los otros dos ángulos.

En el caso particular de un triángulo rectángulo, el coseno se anula y el teorema se reduce al de Pitágoras

$\left(C={\frac {\pi }{2}}\right)\qquad \Rightarrow \qquad c^{2}=a^{2}+b^{2}$

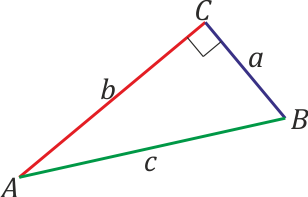
Teorema del seno

El área de un triángulo es la mitad del área de un paralelogramo y por tanto

$A={\frac {1}{2}}\left|{\vec {a}}\times {\vec {b}}\right|={\frac {1}{2}}\left|{\vec {b}}\times {\vec {c}}\right|={\frac {1}{2}}\left|{\vec {a}}\times {\vec {c}}\right|$

Desarrollando los módulos de los productos vectoriales

$A={\frac {ab\,\mathrm {sen} \,C}{2}}={\frac {bc\,\mathrm {sen} \,A}{2}}={\frac {ac\,\mathrm {sen} \,B}{2}}$

Dividiendo por el producto $abc$ y multiplicando por 2 nos queda

${\frac {\mathrm {sen} \,C}{c}}={\frac {\mathrm {sen} \,A}{a}}={\frac {\mathrm {sen} \,B}{b}}$

que es el teorema del seno.