Problemas del primer principio de la termodinámica

Trabajo en una compresión por un peso

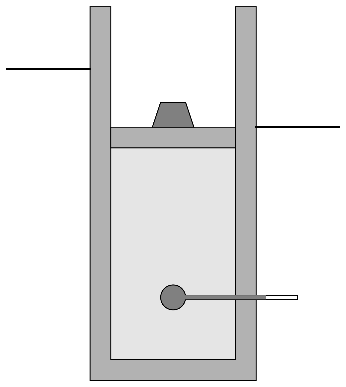
Un tubo vertical de sección cuadrada de 4.0 cm de lado contiene hidrógeno a 300 K y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura.

1. Suponiendo que las paredes del tubo son diatermas, calcule el trabajo realizado sobre el sistema entre el estado inicial y el estado de equilibrio final sí…
   1. Se coloca bruscamente sobre la tapa una pesa de 4.0 kg.
   2. Se colocan sobre el émbolo 4.0 kg de arena grano a grano.
2. Calcule asimismo el trabajo si tras los procesos anteriores se retira el peso extra (o bien retirando la pesa o bien grano a grano).
3. Si consideramos el proceso completo de puesta y retirada del peso (en sus cuatro variantes posibles, según como se combinen), ¿cuál es el trabajo neto en cada uno?

Solución

Compresión en varios pasos

Como caso intermedio del problema “Trabajo en una compresión por un peso”, considere el caso de que en lugar de una pesa de 40 N se coloca primero una de 20 N, se deja que se alcance el equilibrio y se coloca luego otra de 20 N. ¿Cuál es el trabajo en ese caso?

Si en vez de dos pesas, se colocan sucesivamente 5 piezas de 8 N cada una, ¿cuál sería el trabajo?

Obtenga la expresión general para el caso de que se coloquen sucesivamente n pesas de peso (40/n)N. Tome el límite n→∞ y compruebe con el caso cuasiestático del problema citado.

Solución

Energía en una compresión

Para los dos casos del problema “Trabajo en una compresión por un peso”, halle la variación en la energía interna del gas, en la entalpía y el calor que entra en el sistema durante el proceso.

Solución

Compresión adiabática de un gas

Suponga el sistema del problema “Trabajo en una compresión por un peso”, pero admitiendo que las paredes del tubo son adiabáticas. ¿Cómo quedan en ese caso el trabajo, el calor y la variación de la energía interna para los procesos considerados?

Solución

Comparación de tres procesos

Considere los tres procesos de la figura, con $p_{A}=100\,\mathrm {kPa}$, $V_{A}=4\,\mathrm {L}$ y $p_{B}=300\,\mathrm {kPa}$, $V_{A}=1\,\mathrm {L}$.

1. Para los procesos 1 y 2 calcule independientemente el trabajo y el calor que entran en el sistema en cada uno. ¿Cuánto vale la suma del calor y el trabajo en cada uno de los dos procesos?
2. Para el proceso 3, calcule el trabajo en este proceso y, a partir de este, el calor que entra en el sistema.

Solución

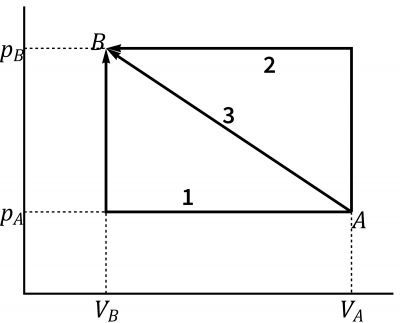
Sucesión de tres procesos cuasiestáticos

Un cilindro de 100 cm² de sección contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático

A→B Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.

B→C Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.

C→A Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.

Para este proceso:

1. Halle la presión, volumen y temperatura al final de cada fase del proceso.
2. Calcule el trabajo en cada fase, así como el trabajo neto total.
3. Calcule la variación en la energía interna y el calor en cada paso y su variación neta.

Solución

Mezcla de dos cantidades de agua

En un recipiente adiabático se ponen en contacto 750 cm³ de agua a 20℃ con 250 cm³ de agua a 80℃, siendo la temperatura exterior de 50°C. ¿Cuál es la temperatura final de la mezcla? ¿Cuánto calor entra en cada subsistema?

Solución

Mezcla de dos cantidades de agua (2)

¿Cómo cambian los resultados del problema “Mezcla de dos cantidades de agua” si las paredes son diatermas?

Solución

Mezcla de dos cantidades de agua (3)

¿Cómo cambian los resultados del problema “Mezcla de dos cantidades de agua” si las paredes son diatermas?

Solución

Mezcla de dos cantidades de agua (4)

Se pone en contacto 1kg de agua a 80 ℃ con una masa m de agua a 20 ℃. ¿Cuál es la temperatura final de la mezcla, en función de m? ¿Cuánto calor entra en la masa m? ¿A qué tienden los resultados si m→∞?

Solución

Trabajo en fusión de hielo

Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0 °C, al cual se le cede lentamente calor a una presión de 101.3 kPa hasta que convierte por completo en agua (densidad de masa 1000 kg/m³). ¿Qué trabajo se realiza sobre el sistema?

Solución

Mezcla de agua y hielo

Dentro de un recipiente adiabático se sumerge un bloque de 100 g de hielo a 0.0 °C en 1.0 litros de agua a 20 °C. Determine si se funde todo el hielo y la temperatura final del sistema. ¿Qué ocurre si en lugar de 100 g se tiene 1.0 kg de hielo?

Solución

Mezcla de vapor de agua y hielo

En un recipiente con paredes adiabáticas y un émbolo móvil de forma que la presión es constante e igual a 101.3 kPa, se ponen en contacto 1.0 m³ de vapor de agua a 115 ℃ con 500 g de hielo a −10 ℃. Determine la temperatura final del sistema.

Dato: La constante específica de los gases ideales para el vapor de agua vale $R_{m}=461.5\,\mathrm {J} /\mathrm {kg} \cdot \mathrm {K}$.

Solución

Mezcla de agua y vapor de agua

Se tiene un recipiente cilíndrico de paredes adiabáticas y con pistón móvil también adiabático, inmerso en un ambiente a 300 K y 101.3 kPa de presión. Dentro del recipiente se ponen en contacto 1 kg de agua a 100 ℃ (“subsistema 1”) con 1 m³ de vapor de agua a 200 ℃ (“subsistema 2”). El agua puede considerarse un líquido incompresible de densidad 958.4 kg/m³. El vapor de agua puede suponerse un gas ideal tal que a 100 ℃ y 101.3 kPa tiene una densidad de masa de 0.598 kg/m³. En todo el rango 100 ℃-200 ℃ su calor específico promedio vale $c_{p}=1.850\,\mathrm {kJ} /\mathrm {kg} \cdot \mathrm {K}$. La entalpía específica de vaporización a 100 ℃ y 101.3 kPa vale 2257 kJ/kg.

1. Calcule, para una vez que se ha alcanzado el equilibrio térmico, qué cantidad de agua y de vapor de agua tenemos en el sistema. ¿Cuál es la proporción de la masa de vapor de agua respecto a la masa total (calidad del vapor)?
2. Calcule la variación de energía interna y de entalpía del sistema completo y de cada subsistema en este proceso, así como el trabajo realizado sobre el sistema completo y sobre cada subsistema.

Solución

Calentamiento de agua con una resistencia

En una cámara con un émbolo móvil se coloca 500 cm³ de agua a 300 K. El exterior se encuentra a una presión de 100 kPa. Se le comunica lentamente calor al agua hasta que se evapora por completo.

1. Calcule el calor necesario para que se realice este proceso.
2. Halle el trabajo que se realiza sobre el agua.
3. Calcule la variación en la entalpía y en la energía interna del agua.
4. Suponga que el calentamiento se produce mediante una resistencia eléctrica a una tensión de 220 V por la que pasa una corriente de 2 A. ¿Cuánto tiempo tarda en realizarse el proceso? En este caso, la energía entra en el sistema en forma de calor o de trabajo?

Solución

Calor y trabajo en un proceso lineal

Considere el caso del problema “Compresión lineal de un gas”, en el que se comprime cuasiestáticamente un gas ideal diatómico que inicialmente se encuentra a presión $p_{A}=100\,\mathrm {kPa}$, temperatura $T_{A}=300\,\mathrm {K}$ y ocupa un volumen $V_{A}=0.01\,\mathrm {m} ^{3}$, según la ley

$p=3p_{A}-{\frac {2p_{A}}{V_{A}}}V$

La compresión continúa hasta que la presión vale $p_{B}=2p_{A}$.

1. Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
2. Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.

Solución

Equilibrio de dos cámaras de aire

Se tiene un sistema formado por dos cámaras de aire seco (γ=1.4). La cámara izquierda (subsistema 1) es rígida. La derecha (subsistema 2) está limitada en su lado derecho por un pistón móvil, siendo la presión externa de 100 kPa. Las paredes exteriores y el pistón son adiabáticos. En el estado inicial, las dos cámaras ocupan 1 litro cada una y la presión de ambas es de 100 kPa, siendo la temperatura de la de la derecha 600 K y la de la izquierda 300 K, que también es la temperatura exterior. La pared entre las dos cámaras no es un aislante perfecto, sino que lentamente el calor va pasando de la cámara caliente a la fría.

1. Calcule la temperatura final de cada una de las dos cámaras.
2. Calcule el trabajo neto que entra, el calor neto que entra, la variación de energía interna y de entalpía para cada uno de los dos subsistemas y para el sistema completo.

Solución

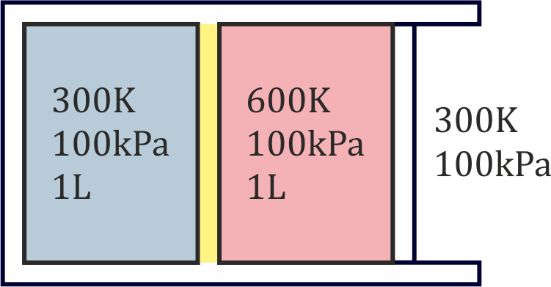
Cuatro procesos no cuasiestáticos

Se tiene un cilindro horizontal cerrado por un pistón, en cuyo interior hay aire seco (considerado un gas ideal diatómico). Inicialmente, el aire interior se encuentra a 450 kPa y 333 K, ocupando un volumen de 1000 cm³. El ambiente se encuentra a 100 kPa y 296 K, valores que no cambian en ningún momento.

Las paredes del cilindro son adiabáticas. El pistón está inicialmente limitado por un tope y forrado de forma que está aislado térmicamente.

Se realiza entonces el siguiente proceso compuesto:

• A→B Se libera bruscamente el tope, dejando que el gas se expanda sin quitarle el aislante térmico.
• B→C Una vez que se ha alcanzado de nuevo el equilibrio y sin volver a fijar la tapa, se quita bruscamente el aislante térmico, dejando que el sistema evolucione.

Ninguno de los dos pasos es cuasiestático.

Para este proceso

a.1 Calcule la presión, volumen y temperatura del gas en los estados B y C.

a.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→B y B→C.

Suponga ahora que, partiendo del mismo estado inicial se realizan los dos desbloqueos en orden inverso, es decir,

• A→D Se quita bruscamente el aislante térmico, sin quitar el tope
• D→E Sin volver a poner el aislante, se libera bruscamente el tope.

Ninguno de los dos pasos es cuasiestático.

Para este nuevo proceso, calcule las mismas magnitudes que en el caso anterior, es decir:

b.1 Calcule la presión, volumen y temperatura del gas en los estados D y E.

b.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→D y D→E.

Solución

Descenso en un proceso cíclico

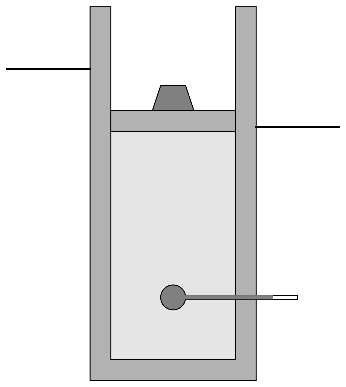
Se construye un sistema de cilindro con pistón, para el cual se sigue el siguiente proceso cíclico. Se parte de un estado A en el que tenemos un cilindro de paredes aisladas térmicamente (aunque el aislante no es perfecto), con pistón. El cilindro tiene 100 cm² de sección y el pistón se halla inicialmente a 70 cm del fondo. El interior del cilindro contiene inicialmente aire seco a 7 ℃ y 100 kPa, que coinciden con la temperatura y la presión del ambiente, las cuales son constantes.

A	B
D	C

A→B

Sobre el pistón se coloca bruscamente una pesa de 250 N, que hace que el pistón descienda una cierta distancia. Este proceso puede suponerse adiabático, pero no cuasiestático.

B→C

Sin quitar la pesa se deja que el gas cambie lentamente su temperatura hasta que se iguala a la temperatura exterior.

C→D

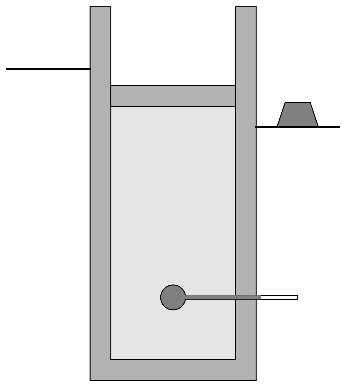
Se quita bruscamente la pesa a la nueva altura, lo que hace que el pistón suba bruscamente, en otro proceso adiabático no cuasiestático.

D→A

Se deja que el aire ceda o absorba calor lentamente hasta que vuelve a estar a la temperatura inicial y en la posición de partida.

Para este ciclo:

1. Calcule la presión, temperatura y volumen del aire en cada estado. ¿Cuántos cm desciende la pesa entre los estados A y C?
2. Indique gráficamente en un diagrama pV, de manera aproximada, cómo es el ciclo localizando los cuatro estados y trazando aquellos procesos que se puedan representar.
3. Calcule el trabajo y el calor que entra en el sistema en cada paso, así como el trabajo neto de entrada y el calor neto de salida en el ciclo.

Solución

Compresión lineal con calor nulo

Una cierta cantidad de aire seco experimenta una compresión cuasiestática A→B que se describe en un diagrama pV con un segmento rectilíneo como el de la figura. Sean $V_{A}=1200\,\mathrm {cm} ^{3}$, $p_{A}=102\,\mathrm {kPa}$ y $T_{A}=297\,\mathrm {K}$ las condiciones iniciales y$V_{A}/V_{B}=r=3$ la relación de compresión.

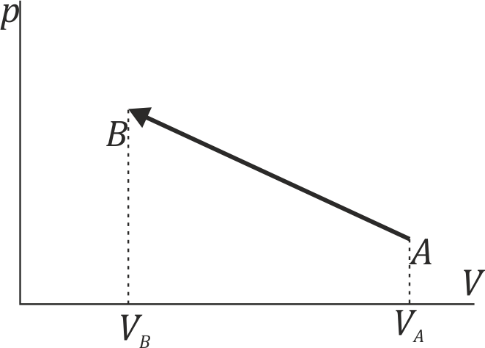
1. Calcule el trabajo realizado sobre el sistema en el proceso A→B como función de la presión final $p_{B}$ y del resto de datos del problema.
2. Halle el valor de la presión final $p_{B}$ si en el proceso descrito el calor neto que entra en el sistema es nulo, $Q_{A\to B}=0$, es decir, el proceso no es adiabático, sino que el calor que entra iguala al que sale.
3. Halle la temperatura final $T_{B}$ en el proceso anterior.

Solución

Expansión lineal de un gas ideal diatómico

Se tiene una cantidad fija de un gas ideal diatómico situada a una presión $p_{0}$, volumen $V_{0}$ y temperatura $T_{0}$. Experimenta un proceso tal que la presión final es $2p_{0}$ y el volumen $2V_{0}$.

1. ¿Cuánto vale el incremento de la energía interna en este proceso?
2. Supongamos que el proceso anterior ocurre de manera cuasiestática según la ley $p(V)=(p_{0}/V_{0})V$ ¿Cuánto trabajo se realiza sobre el gas en esta expansión cuasiestática? ¿Cuánto calor entra en el gas en la expansión cuasiestática?

Solución