Problemas de dinámica impulsiva (CMR)

Percusión sobre una mancuerna

Supongamos dos masas iguales $m/2$ unidas por una barra rígida de longitud $2b$, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. Se comunica una percusión ${\vec {P}}$ perpendicular a la barra a una distancia $c$ de su centro.

1. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra tras la percusión?
2. ¿Dónde se encuentra el centro instantáneo de rotación justo tras la percusión?
3. ¿Cómo es el movimiento del sistema a partir de ese momento?

Solución

Percusión sobre una barra

¿Cómo cambian los resultados del problema anterior si en lugar de una mancuerna tenemos una barra homogénea de longitud $2b$ y masa $m$ a la cual se comunica una percusión ${\vec {P}}$ perpendicular a la barra a una distancia $c$ de su centro?

Solución

Percusión sobre una barra articulada

¿Cómo cambian los resultados de los dos problemas anteriores si la barra está articulada a un punto fijo O, situado en uno de los extremos de la barra? ¿Cuánto valen las percusiones y momentos impulsivos de reacción en O?

¿Y sí en lugar de estar articulada, está empotrada en O?

Solución

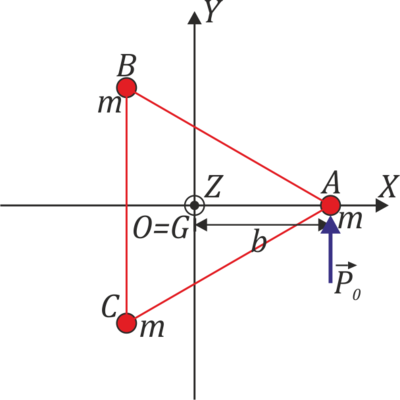
Percusión en sistema de tres masas

Un sólido está formado por tres masas iguales $m$ unidas por varillas rígidas de la misma longitud, de masa despreciable. El triángulo se encuentra situado sobre un plano horizontal, sin rozamiento. Se elige un sistema de ejes tal que el baricentro del triángulo es el origen de coordenadas y la masa A se encuentra en $b{\vec {\imath }}$, hallándose las masas B y C en las posiciones correspondientes del plano OXY. Estando el triángulo en reposo, se golpea la masa A con una percusión ${\vec {P}}=P_{0}{\vec {\jmath }}$. Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas):

1. La velocidad del centro de masas del triángulo.
2. La velocidad angular del triángulo.
3. La velocidad de cada una de las masas.
4. La posición del centro instantáneo de rotación.
5. Calcule los valores de las percusiones de reacción que se producen en las tres varillas en el momento en que se aplica la percusión ${\vec {P}}_{0}$.

Solución

Percusión sobre una barra. Estudio analítico

Suponga una barra homogénea, de masa $m$ y longitud $b$, situada horizontalmente sobre un plano sin rozamiento.

Estando la barra en reposo, se efectúa sobre ella una percusión ${\vec {P}}_{0}$ perpendicular a la dirección de la barra y a una distancia c de su centro.

Empleando las técnicas de la mecánica analítica, determine la velocidad del centro de la barra y la velocidad angular de ésta, así como las posibles fuerzas y momentos impulsivos de reacción, en los casos siguientes:

1. La barra puede moverse libremente por el plano.
2. La barra se halla articulada por un extremo A a una pared inmóvil.
3. La barra se halla empotrada por su extremo A a una pared inmóvil.

Percusión sobre un sistema articulado

Considerando el sistema de dos barras articuladas del problema “dos barras articuladas” suponga que el sistema se halla completamente extendido y en reposo. Entonces, se efectúa una percusión ${\vec {P}}_{0}$ perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.

Determine la velocidad angular de cada barra, así como la velocidad de los puntos A y B (extremo libre de la segunda barra) en los casos:

1. Se golpea la barra OA en un punto D a una distancia c de la articulación A.
2. Se golpea la barra AB en un punto D a una distancia c de la articulación A.

Percusión sobre una barra con resorte

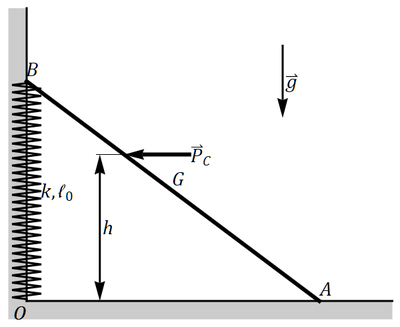
Se tiene un sistema formado por una varilla de masa $m=1.2\,\mathrm {kg}$ y longitud $b=1\,\mathrm {m}$, apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared está conectado a la esquina mediante un resorte de constante $k=30\,\mathrm {N} /\mathrm {m}$ y longitud natural $\ell _{0}=1\,\mathrm {m}$. Por efecto de la gravedad (tómese $g=10\,\mathrm {m} /\mathrm {s} ^{2}$) la varilla resbala hasta que la compresión del resorte la detiene.

1. Determine la posición de los extremos A y B de la barra en la posición de equilibrio.
2. Suponiendo que se encuentra en la posición de equilibrio, se efectúa sobre la barra una percusión horizontal en un punto C a una altura $h=20\,\mathrm {cm}$ y de magnitud ${\vec {P}}_{C}=-1.5\,{\vec {\imath }}\,\mathrm {N} \cdot \mathrm {s} .$ Calcule la velocidad del centro de masas inmediatamente después de la percusión, así como las percusiones de reacción en la pared y el suelo.
3. Tras la percusión anterior, la varilla se acerca a la pared. Calcule la velocidad del centro de masas de la varilla en el momento en que impacta con la pared.

Percusión sobre una barra articulada con muelle

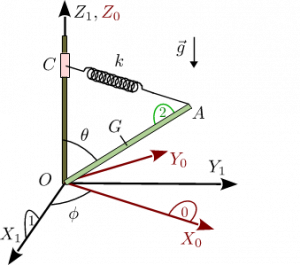
El mecanismo de la figura está formado por una varilla delgada $OA$ (sólido "2"), de masa $m$ y longitud $L$, y un resorte ideal de constante recuperadora $k$ y longitud natural nula. El extremo $O$ de la varilla está unido mediante una rótula ideal al origen de un sistema de referencia fijo $OX_{1}Y_{1}Z_{1}$ (sólido "1"). El otro extremo $A$ de la varilla está conectado mediante el resorte a un pasador $C$ de masa despreciable que puede deslizar libremente y sin rozamiento por el eje vertical $OZ_{1}$. En todo momento la orientación del eje del resorte es perpendicular a $OZ_{1}$. Todos los vínculos son lisos. En el instante inicial $t=0$, el sistema se halla en reposo en la posición $\theta (0)=\pi /4$, $\phi (0)=0$. Recibe entonces una percusión ${\vec {\hat {F}}}=[{\hat {F}}_{x},\,{\hat {F}}_{y},\,0]_{1}$ en el extremo $A$. Justo después de la percusión tenemos ${\dot {\theta }}(0^{+})=3\Omega /{\sqrt {2}}$, ${\dot {\phi }}(0^{+})=3{\sqrt {2}}\Omega$, donde $\Omega$ es una constante conocida. Calcula el valor de la percusión.

Barra oscilante sometida a una percusión horizontal

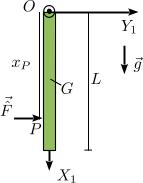
Una barra homogénea de longitud $L$ está articulada en un punto fijo $O$ de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia $x_{P}$ del punto $O$. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica.

Disco rodando sobre plataforma con muelle

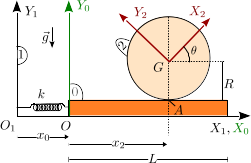
Un disco de masa $m$ y radio $R$ (sólido "2") rueda sin deslizar sobre una placa rectangular de masa $m$ (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo $O_{1}X_{1}$. Un muelle de constante elástica $k$ y longitud natural nula conecta la placa con el eje $O_{1}Y_{1}$.

1. Encuentra la reducción cinemática del movimiento absoluto.
2. Escribe la Lagrangiana del sistema.
3. Escribe las ecuaciones de Lagrange.
4. En el estado inicial los dos sólidos están en reposo y $x_{0}(0)=0$, $x_{2}(0)=L/2$. Se somete la placa a una percusión ${\vec {\hat {F}}}={\hat {F}}_{0}\,{\vec {\imath }}_{1}$ aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión?