Percusión en sistema de tres masas

Enunciado

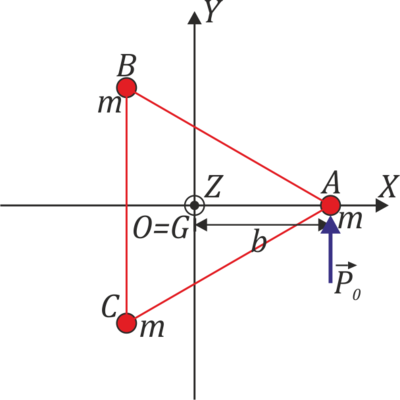
Un sólido está formado por tres masas iguales $m$ unidas por varillas rígidas de la misma longitud, de masa despreciable. El triángulo se encuentra situado sobre un plano horizontal, sin rozamiento. Se elige un sistema de ejes tal que el baricentro del triángulo es el origen de coordenadas y la masa A se encuentra en $b{\vec {\imath }}$, hallándose las masas B y C en las posiciones correspondientes del plano OXY. Estando el triángulo en reposo, se golpea la masa A con una percusión ${\vec {P}}=P_{0}{\vec {\jmath }}$. Para el instante inmediatamente posterior a la percusión determine (empleando mecánica vectorial o analítica o ambas):

1. La velocidad del centro de masas del triángulo.
2. La velocidad angular del triángulo.
3. La velocidad de cada una de las masas.
4. La posición del centro instantáneo de rotación.
5. Calcule los valores de las percusiones de reacción que se producen en las tres varillas en el momento en que se aplica la percusión ${\vec {P}}_{0}$.

Velocidad del CM

El sistema describe un movimiento plano. Las velocidades de las tres partículas se gallan sobre el plano OXY, mientras que la velocidad angular apunta en la dirección de OZ. Esto permite simplificar los cálculos.

El teorema de la cantidad de movimiento, aplicada a percusiones da

$\Delta {\vec {p}}=m_{T}({\vec {v}}_{G}^{\,+}-\overbrace {{\vec {v}}_{G}^{\,-}} ^{={\vec {0}}})={\vec {P}}_{0}$

siendo la masa total $m_{T}=3m$. Por tanto

${\vec {v}}_{G}^{\,+}={\dfrac {P_{0}}{3m}}{\vec {\jmath }}$

Velocidad angular

El teorema del momento cinético para percusiones da

$\Delta {\vec {L}}_{O}=I({\vec {\omega }}^{\,+}-\overbrace {{\vec {\omega }}^{\,-}} ^{={\vec {0}}})={\overrightarrow {OA}}\times {\vec {P}}_{0}$

Dado que las tres masas están la misma distancia del origen, el momento de inercia vale, simplemente

$I=I_{zz}=3mb^{2}\,$

mientras que el momento de la percusión es

${\overrightarrow {OA}}\times {\vec {P}}_{0}=(b{\vec {\imath }})\times (P_{0}{\vec {\jmath }})=bP_{0}{\vec {k}}$

lo que nos da la velocidad angular

${\vec {\omega }}^{\,+}={\dfrac {P_{0}}{3mb}}{\vec {k}}$

Velocidad de cada masa

Una vez que tenemos la velocidad de un punto, el centro de masas situado en el origen, y la velocidad angular podemos determinar la velocidad de cualquier otro punto.

Las tres masas se encuentran localizadas en

${\begin{array}{rcl}{\overrightarrow {OA}}&=&b{\vec {\imath }}\\&&\\{\overrightarrow {OB}}&=&b(\cos(120^{\circ }){\vec {\imath }}+\mathrm {sen} (120^{\circ }){\vec {\jmath }})=-{\dfrac {b}{2}}{\vec {\imath }}+{\dfrac {b{\sqrt {3}}}{2}}{\vec {\jmath }}\\&&\\{\overrightarrow {OC}}&=&b(\cos(240^{\circ }){\vec {\imath }}+\mathrm {sen} (240^{\circ }){\vec {\jmath }})=-{\dfrac {b}{2}}{\vec {\imath }}-{\dfrac {b{\sqrt {3}}}{2}}{\vec {\jmath }}\end{array}}$

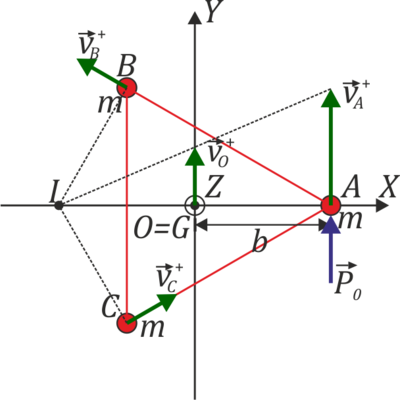
A se mueve con la velocidad

${\vec {v}}_{A}^{\,+}={\vec {v}}_{O}^{\,+}+{\vec {\omega }}^{\,+}\times {\overrightarrow {OA}}={\dfrac {P_{0}}{3m}}{\vec {\jmath }}+{\dfrac {P_{0}}{3mb}}{\vec {k}}\times (b{\vec {\imath }})={\dfrac {2P_{0}}{3m}}{\vec {\jmath }}$

B lo hace con

${\vec {v}}_{B}^{\,+}={\vec {v}}_{O}^{\,+}+{\vec {\omega }}^{\,+}\times {\overrightarrow {OB}}={\dfrac {P_{0}}{3m}}{\vec {\jmath }}+{\dfrac {P_{0}}{3mb}}{\vec {k}}\times \left(-{\dfrac {b}{2}}{\vec {\imath }}+{\dfrac {b{\sqrt {3}}}{2}}{\vec {\jmath }}\right)={\dfrac {P_{0}}{3m}}\left(-{\dfrac {\sqrt {3}}{2}}{\vec {\imath }}+{\frac {1}{2}}{\vec {\jmath }}\right)$

y C

${\vec {v}}_{C}^{\,+}={\vec {v}}_{O}^{\,+}+{\vec {\omega }}^{\,+}\times {\overrightarrow {OC}}={\dfrac {P_{0}}{3m}}{\vec {\jmath }}+{\dfrac {P_{0}}{3mb}}{\vec {k}}\times \left(-{\dfrac {b}{2}}{\vec {\imath }}-{\dfrac {b{\sqrt {3}}}{2}}{\vec {\jmath }}\right)={\dfrac {P_{0}}{3m}}\left({\dfrac {\sqrt {3}}{2}}{\vec {\imath }}+{\frac {1}{2}}{\vec {\jmath }}\right)$

Posición del C.I.R.

La posición del CIR puede determinarse gráficamente, a partir de la velocidad de dos puntos, o analíticamente, a partir de la velocidad de un punto y la velocidad angular

${\overrightarrow {OI}}={\dfrac {{\vec {k}}\times {\vec {v}}_{O}^{\,+}}{\omega ^{+}}}={\dfrac {{\vec {k}}\times ((P_{0}/3m){\vec {\jmath }})}{P_{0}/3mb}}=-b{\vec {\imath }}$

El centro instantáneo de rotación, justo tras la percusión, se halla en el punto opuesto a A por el origen.

Percusiones de reacción

Cuando la percusión se produce sobre A, los puntos B y C comienzan también a moverse porque las varillas producen percusiones de reacción sobre ellas. Cada masa está sujeta entonces a dos percusiones de reacción, que además cumplen la 3ª ley de Newton.

${\vec {P}}_{B\to A}=-{\vec {P}}_{A\to B}$

Estas percusiones van dirigidas a lo largo de cada varilla, de forma que

${\vec {P}}_{A\to B}=P_{AB}{\vec {u}}_{AB}=P_{AB}\left(-{\dfrac {\sqrt {3}}{2}}{\vec {\imath }}+{\dfrac {1}{2}}{\vec {\jmath }}\right)\qquad \qquad {\vec {P}}_{B\to A}=-{\vec {P}}_{A\to B}$

Análogamente

${\vec {P}}_{A\to C}=P_{AC}{\vec {u}}_{AC}=P_{AC}\left(-{\dfrac {\sqrt {3}}{2}}{\vec {\imath }}-{\dfrac {1}{2}}{\vec {\jmath }}\right)\qquad \qquad {\vec {P}}_{C\to A}=-{\vec {P}}_{A\to C}$

y

${\vec {P}}_{C\to B}=P_{CB}{\vec {u}}_{CB}=P_{CB}{\vec {\jmath }}\qquad \qquad {\vec {P}}_{B\to C}=-{\vec {P}}_{C\to B}$

El punto A está sometido además a la percusión externa.

Si aplicamos el teorema de la cantidad de movimiento al punto A nos queda

$m{\vec {v}}_{A}^{\,+}={\vec {P}}_{0}+{\vec {P}}_{B\to A}+{\vec {P}}_{C\to A}\qquad \qquad \left\{{\begin{array}{rcrcl}x:&\ &0&=&P_{AB}{\dfrac {\sqrt {3}}{2}}+P_{AC}{\dfrac {\sqrt {3}}{2}}\\&&&&\\y:&\ &{\dfrac {2P_{0}}{3}}&=&-{\dfrac {P_{AB}}{2}}+{\dfrac {P_{AC}}{2}}\end{array}}\right.$

lo que nos da

$P_{AB}={\dfrac {P_{0}}{3}}\qquad \qquad P_{AC}=-{\dfrac {P_{0}}{3}}$

Aplicamos ahora el teorema a la masa B

$m{\vec {v}}_{B}^{\,+}={\vec {P}}_{A\to B}+{\vec {P}}_{C\to B}\qquad \qquad \left\{{\begin{array}{rcrcl}x:&\ &-{\dfrac {P_{0}{\sqrt {3}}}{6}}&=&-P_{AB}{\dfrac {\sqrt {3}}{2}}\\&&&&\\y:&\ &{\dfrac {P_{0}}{6}}&=&{\dfrac {P_{AB}}{2}}+P_{CB}\end{array}}\right.$

Si sustituimos el valor de $P_{AB}$ nos queda

$P_{CB}=0\,$

Aplicando el mismo teorema a la masa C resultan los mismos valores, como cabe esperar.

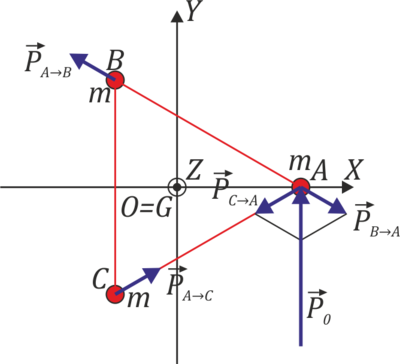
Por tanto tenemos que la percusión hace que A empuje a B (y esa varilla está en compresión), mientras tira de C (y esa varilla está en tracción), mientras que en la varilla BC no se produce percusión.