Disco rodando sobre plataforma con muelle (Ene 2018 MR)

Enunciado

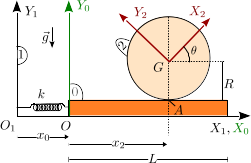
Un disco de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} y radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} (sólido "2") rueda sin deslizar sobre una placa rectangular de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O_1X_1} . Un muelle de constante elástica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula conecta la placa con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O_1Y_1} .

1. Encuentra la reducción cinemática del movimiento absoluto.
2. Escribe la Lagrangiana del sistema.
3. Escribe las ecuaciones de Lagrange.
4. En el estado inicial los dos sólidos están en reposo y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_0(0)=0} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_2(0)=L/2} . Se somete la placa a una percusión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\hat{F}} = \hat{F}_0\,\vec{\imath}_1} aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión?

Solución

Reducción cinemática

Movimiento {01}

La placa realiza una traslación. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{01} = \vec{0}, \qquad \vec{v}_{01} = \dot{x}_0\,\vec{\imath}_1. }

Movimiento {20}

El disco rueda sin deslizar sobre la placa. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20} = \omega_{20}\,\vec{k}, \qquad \vec{v}^{\,G}_{20} = \dot{x}_2\,\vec{\imath}_1, \qquad \vec{v}^{\,A}_{20} = \vec{0}. }

Aplicando el Teorema de Chasles entre los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} tenemos

${\vec {v}}_{20}^{\,G}={\vec {v}}_{20}^{\,A}+{\vec {\omega }}_{20}\times {\overrightarrow {AG}}=(\omega _{20}\,{\vec {k}})\times (R\,{\vec {\jmath }}_{1})=-R\omega _{20}\,{\vec {\imath }}_{1}.$

Comparando obtenemos

${\vec {\omega }}_{20}=-{\dfrac {{\dot {x}}_{2}}{R}}\,{\vec {k}}.$

Movimiento {21}

Usamos la composición {21} = {20} + {01}. Tenemos

${\begin{array}{l}{\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}=-{\dfrac {{\dot {x}}_{2}}{R}}\,{\vec {k}},\\\\{\vec {v}}_{21}^{\,G}={\vec {v}}_{20}^{\,G}+{\vec {v}}_{01}^{\,G}=({\dot {x}}_{0}+{\dot {x}}_{2})\,{\vec {\imath }}_{1}.\end{array}}$

Vemos que el sistema tiene dos grados de libertad, elegidos aquí como $\{x_{0},x_{2}\}$.

Lagrangiana

Energía cinética

La placa hace una traslación, por lo que su energía cinética es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T_{0} = \dfrac{1}{2}m|\vec{v}_{01}|^2 = \dfrac{1}{2}m\dot{x}_0^2. }

Como hace un movimiento plano, la energía cinética del disco es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T_2 = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}I_G|\vec{\omega}_{21}|^2. }

El momento de inercia es $I_{G}=mR^{2}/2$. Entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T_2 =\dfrac{1}{2}m\left(\dot{x}_0 + \dot{x}_2\right)^2 + \dfrac{1}{4}m\dot{x}_2^2. }

Entonces la energía cinética total es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T = T_0 + T_2 = m\dot{x}_0^2 + m\dot{x}_0\dot{x}_2 + \dfrac{3}{4}m\dot{x}_2^2. }

Energía pontencial

Los centros de masas de los dos sólidos están siempre a la misma altura. Entonces su energía potencial gravitatoria es constante y no interviene en la dinámica del problema. El muelle aporta una energía potencial elástica

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U = \dfrac{1}{2}kx_0^2. }

Función de Lagrange

Con esto, la función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle L = T - U = m\dot{x}_0^2 + m\dot{x}_0\dot{x}_2 + \dfrac{3}{4}m\dot{x}_2^2 - \dfrac{1}{2}kx_0^2. }

Ecuaciones de Lagrange

Ecuación para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_0}

Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{x}_0}\right) -\dfrac{\partial L}{\partial x_0} = 0 \Longrightarrow m\ddot{x}_2 + 2m\ddot{x}_0 + k x_0 = 0. \quad(1) }

Ecuación para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_2}

Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{x}_2}\right) -\dfrac{\partial L}{\partial x_2} = 0 \Longrightarrow m\ddot{x}_0 + \dfrac{3}{2}m\ddot{x}_2 = 0. \quad (2) }

Percusión

Las ecuaciones de Lagrange percusivas son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta p_{x_0} = \hat{Q}_{x_0}, \qquad \Delta p_{x_2} = \hat{Q}_{x_2} }

Los momentos generalizados son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} p_{x_0} = \dfrac{\partial L}{\partial \dot{x}_0} = 2m\dot{x}_0 + m\dot{x}_2, \\ \\ p_{x_2} = \dfrac{\partial L}{\partial \dot{x}_2} = m\dot{x}_0 + \dfrac{3}{2}m\dot{x}_2. \end{array} }

Sus variaciones son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \Delta p_{x_0} = 2m\Delta \dot{x}_0 + m\Delta\dot{x}_2 = 2m\dot{x}_0^+ + m\dot{x}_2^+, \\ \\ \Delta p_{x_2} = m\Delta \dot{x}_0 + \dfrac{3}{2}m\Delta\dot{x}_2 = m\dot{x}_0^+ + \dfrac{3}{2} m\dot{x}_2^+. \end{array} }

Hemos usado que los dos sólidos estaban en reposo antes de la percusión.

La percusión se placa en el lado izquierdo de la placa. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \hat{Q}_{x_0} = \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}_{01}}{\partial \dot{x}_0} = \hat{F}_0, \\ \\ \hat{Q}_{x_2} = \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}_{01}}{\partial \dot{x}_2} = 0. \end{array} }

Despejando llegamos a

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{x}^+_0 = \dfrac{3\hat{F}_0}{4m}, \qquad \dot{x}^+_2 = -\dfrac{\hat{F}_0}{2m}. }

A pesar de ese signo negativo, el movimiento absoluto del centro del justo después de la percusión es hacia la derecha (suponiendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \hat{F}_0>0} )

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,G+}_{21} = (\dot{x}^+_0 + \dot{x}^+_2)\,\vec{\imath}_1 = \dfrac{\hat{F}_0}{4m}\,\vec{\imath}_1. }

Después de la percusión el movimiento está controlado por las ecuaciones (1) y (2). Podemos despejar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \ddot{x}_2} de (2) para obtener

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \ddot{x}_0 = -\dfrac{3k}{4m}\,x_0. }

Esta es la ecuación de un movimiento armónico simple de frecuencia angular

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle w = \sqrt{\dfrac{3k}{4m}}. }