Problemas de electrostática en medios materiales (GIOI)

Acumulación de carga en un conductor

Sobre una lámina metálica de cobre, de 1m² de área y 1cm de espesor se aplica perpendicularmente un campo eléctrico de 1V/m de intensidad. Calcule cuantos electrones se acumulan en la cara del conductor cargada negativamente. ¿Qué proporción suponen estos electrones respecto al total de electrones disponibles, que en el caso del cobre, es 1 por átomo?

Solución

Esfera conductora en equilibrio electrostático

Se tiene una esfera metálica maciza de radio $a$ y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total $Q$ calcule:

1. el potencial y el campo eléctrico en todos los puntos del espacio.
2. el voltaje al que se encuentra
3. la densidad superficial de carga.
4. la energía electrostática que almacena.
5. Particularice los resultados anteriores para un radio $a=10\,\mathrm {cm}$ y una carga $Q=36\,\mathrm {nC}$.

Solución

Esfera conductora en equilibrio electrostático (II)

Suponga que en el problema “Esfera conductora en equilibrio electrostático”lo que se conoce inicialmente su voltaje $V_{0}$, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje $V_{0}=1.8\,\mathrm {kV}$.

Solución

Energía en la carga de un conductor

Un determinado sistema está formado exclusivamente por un conductor de capacidad C. Inicialmente este conductor almacena una carga $Q_{A}$. Una fuente de tensión continua $V_{B}$ se conecta al conductor mediante un interruptor que se cierra bruscamente.

1. ¿Cuánto cambia la carga almacenada en el conductor?
2. ¿Cuánto cambia la energía electrostática del sistema?
3. ¿Qué trabajo realiza la fuente en este proceso? ¿Cuánta energía se disipa?

Solución

Energía en la carga de un conductor (II)

Suponga ahora que, en el problema anterior, la fuente es una de tensión regulable que se hace variar lentamente desde $V_{A}$ (la correspondiente al estado inicial) a $V_{B}$. ¿Cómo quedan en ese caso las respuestas a los tres apartados?

Solución

Dos esferas conductoras concéntricas

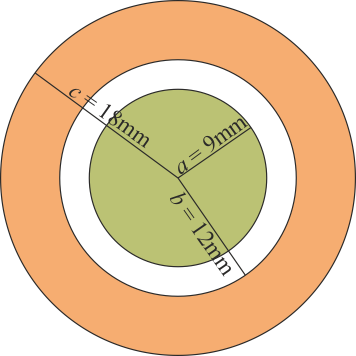
Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle:

1. la carga almacenada en cada conductor
2. el potencial al que se encuentra cada conductor
3. la energía almacenada en el sistema

para los siguientes casos:

1. La esfera almacena una carga de +4 nC y la corona está aislada y descargada.
2. La esfera está aislada y descargada y la corona almacena +6 nC
3. La esfera almacena una carga de +4 nC y la corona de +6 nC
4. La esfera almacena una carga de −4 nC y la corona de +4 nC
5. La esfera almacena una carga de −4 nC y la corona de +6 nC
6. La esfera almacena una carga de +4 nC y la corona está a tierra.
7. La esfera está a tierra y la corona almacena una carga de +6 nC.
8. La esfera está a +2 kV y la corona está a tierra.
9. La esfera está a tierra y la corona a +2 kV.
10. La esfera y la corona están a +2 kV
11. La esfera está a +2 kV y la corona está a −2 kV.

Sugerencia: Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente.

Solución

Conexión de dos esferas alejadas

Se tiene un conductor formado por dos esferas de radios $a$ y $b$ ($a<b$), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga $Q_{0}$.

1. ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
2. ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?
3. Suponga que inicialmente la esfera grande almacena una carga $Q_{0}$ y la pequeña una carga nula, estando el cable desconectado. Se conecta el cable y se espera hasta que se alcance de nuevo el equilibrio electrostático. ¿Cuánto varía la energía almacenada en el sistema? ¿A qué se debe esta diferencia en la energía?

Solución

Triángulo de esferas conductoras

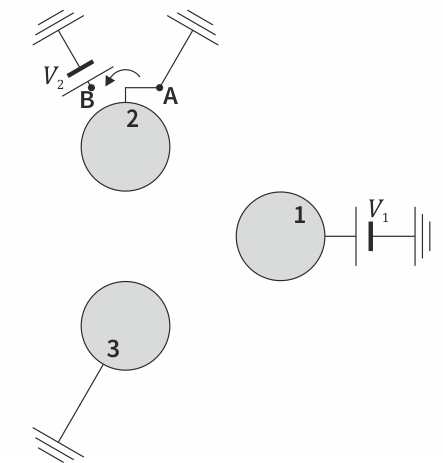
Un sistema de conductores está formado por tres esferas metálicas idénticas de radio b, situadas en los vértices de un triángulo equilátero de lado a ($a>2b$). No hay más conductores ni cargas en el sistema.

Se encuentra experimentalmente que cuando la esfera “1” se encuentra a 10 kV y la “2” y la “3” a tierra, la carga de la propia esfera “1” es de +8 nC, mientras que la de la “2” es de −3 nC.

1. Calcule la energía eléctrica almacenada en el sistema.
2. Dibuje el circuito equivalente y calcule las capacidades de sus condensadores.

Suponga que, sin tocar las esferas 1 y 3, se pasa el interruptor de la esfera 2 a la posición B, de manera que su voltaje pasa a ser de 5kV. Una vez que se llega al equilibrio:

3. ¿Cuál es la nueva carga de cada esfera?
4. ¿Y la energía almacenada?
5. ¿Qué trabajo realiza en el proceso el generador conectado a la esfera 1 y el conectado a la esfera 2?

Solución

Tres placas conductoras paralelas

Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm y ésta de la tercera 0.8 mm. Entre las placas hay un dieléctrico de permitividad $\varepsilon =40\,\mathrm {pF} /\mathrm {m}$. HalleHalle:

1. La carga almacenada en cada placa.
2. El potencial al que se encuentra cada una.
3. El campo eléctrico entre las placas.
4. La energía almacenada en el sistema.

para los siguientes casos:

• La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra.
• La placa central está a 24 V y las otras dos a tierra.
• La primera está a −24 V, la central a +24 V y la tercera a tierra.
• La placa central almacena una carga de 4 nC y las dos placas exteriores están conectadas entre sí.

Solución

Asociación de tres condensadores

Dado el sistema de tres condensadores de la figura,

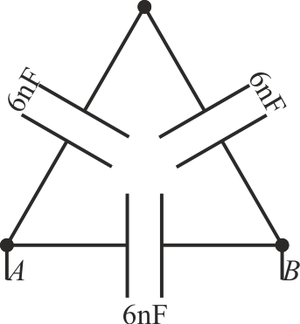
¿cuánto vale la capacidad equivalente entre A y B?

Solución

Carga frente a esfera

Una esfera conductora se encuentra conectada a tierra. Frente a ella se coloca una carga puntual positiva. No hay más cargas ni conductores en el sistema. ¿Qué signo tienen el potencial y la carga de la esfera?

Solución

Carga frente a esfera (II)

¿Cómo cambian los resultados del problema anterior si la esfera se halla aislada y descargada?

Solución

Dos conductores enfrentados

Se colocan dos conductores uno frente al otro. El primero tiene $Q_{1}>0$ y el segundo $Q_{2}=0$. No hay más cargas ni conductores en el sistema. ¿Qué signos tienen sus potenciales?

Solución

Dos conductores enfrentados (II)

Se colocan dos conductores uno frente al otro. El primero tiene $V_{1}>0$ y el segundo $V_{2}=0$. No hay más cargas ni conductores en el sistema. ¿Qué signos tienen sus cargas?

Solución

Sistema de tres conductores

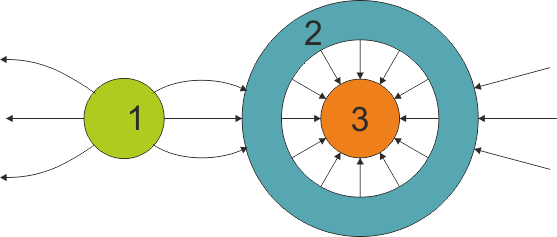
En un sistema de tres conductores, el esquema de las líneas de campo es aproximadamente como el de la figura.

1. ¿Cuál de los tres conductores está a mayor potencial? ¿Cuál a menor? ¿Es negativo o nulo alguno de ellos?
2. ¿Cómo es el circuito equivalente que representa este sistema?

Solución

Sistema de cuatro condensadores

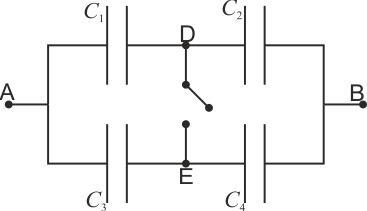
El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: $C_{1}=30\,\mathrm {nF}$, $C_{2}=60\,\mathrm {nF}$, $C_{3}=120\,\mathrm {nF}$ y $C_{4}=40\,\mathrm {nF}$. La diferencia de potencial entre A y B es de $12\,\mathrm {V}$.

1. ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E?
2. Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
3. Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?

Solución

Transformación Δ-Y (delta-estrella)

En la transformación Δ-Y (delta-estrella) se trata de relacionar dos sistemas equivalentes. En la configuración delta tenemos tres condensadores formando un triángulo entre tres nodos. En la configuración en estrella tenemos tres condensadores unidos a un nodo central descargado.

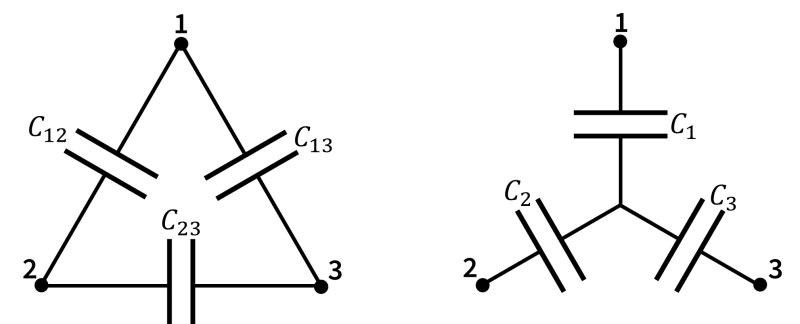
1. Demuestre que dadas las capacidades de la estrella $C_{1}$, $C_{2}$ y $C_{3}$, las capacidades de la delta $C_{12}$, $C_{13}$ y $C_{23}$ vienen dadas por

${\begin{array}{ccccc}C_{12}={\dfrac {C_{1}C_{2}}{S}}&\qquad &C_{13}={\dfrac {C_{1}C_{3}}{S}}&\qquad &C_{23}={\frac {C_{2}C_{3}}{S}}\\&&&&\\&&S=C_{1}+C_{2}+C_{3}&&\end{array}}$

1. Demuestre las relaciones inversas: dadas las capacidades de la delta, $C_{12}$, $C_{13}$ y $C_{23}$, las capacidades de la estrella, $C_{1}$, $C_{2}$ y $C_{3}$. vienen dadas por

${\begin{array}{ccccc}C_{1}={\dfrac {P}{C_{23}}}&\qquad &C_{2}={\dfrac {P}{C_{13}}}&\qquad &C_{3}={\dfrac {P}{C_{12}}}\\&&&&\\&&P=C_{12}C_{13}+C_{12}C_{23}+C_{13}C_{23}&&\end{array}}$

1. Calcule la configuración en estrella equivalente a una configuración delta en la que las capacidades valen $C_{12}=20\,\mathrm {nF}$, $C_{13}=30\,\mathrm {nF}$, $C_{23}=12\,\mathrm {nF}$.
2. Calcule la configuración en delta equivalente a una configuración en estrella en la cual $C_{1}=100\,\mathrm {pF}$, $C_{2}=400\,\mathrm {pF}$,$C_{3}=500\,\mathrm {pF}$.
3. Para los dos apartados anteriores, suponga que $V_{1}=10\,\mathrm {V}$, $V_{2}=5\,\mathrm {V}$, $V_{3}=0\,\mathrm {V}$. Para las dos configuraciones equivalentes calcule la energía almacenada y compruebe que se llega al mismo resultado.

Solución

Sistema de 5 condensadores

Se tiene el sistema de 5 condensadores de la figura. Calcule la capacidad equivalente entre los nodos de los extremos A y B.

Solución

Condensador que se rellena de dieléctrico

El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.

Entre las placas se establece una diferencia de potencial de 20 V

1. ¿Cuánto vale la energía almacenada en el sistema?
2. Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato ($\varepsilon _{r}=3.3$) de 3 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
3. Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?

Solución

Condensador con dos capas de dieléctrico

Se tiene el condensador de la figura, formado por dos placas conductoras paralelas de sección $S$ y distancia entre placas $a$. Entre ellas la mitad del espacio está ocupado por un dieléctrico ideal de permitividad relativa 1.5 y la otra mitad por uno de permitividad 3.0, siendo la frontera paralela a las placas. La capacidad del condensador en vacío en ausencia de los dieléctricos es $C_{0}$.

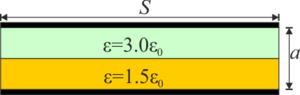
1. ¿Cuánto vale la capacidad de este condensador?
2. Suponga que este condensador se conecta a una fuente de tensión $V_{0}$. Si $E_{1}$ es el campo en el material de permitividad 1.5 y $E_{2}$ en el de permitividad 3.0, ¿en cuál de las dos regiones es más intenso el campo eléctrico? ¿O son iguales?

Solución

Condensador con dos bloques de dieléctrico

¿Cómo cambian las respuestas del problema “Condensador con dos capas de dieléctrico” si la frontera entre los dos dieléctricos es perpendicular a las placas, de manera que la mitad de la izquierda está ocupada por el dieléctrico de permitividad relativa $\varepsilon _{1}=3.0$ y la de la derecha por el de permitividad $\varepsilon _{2}=1.5$?

Solución

Sistema de tres conductores esféricos

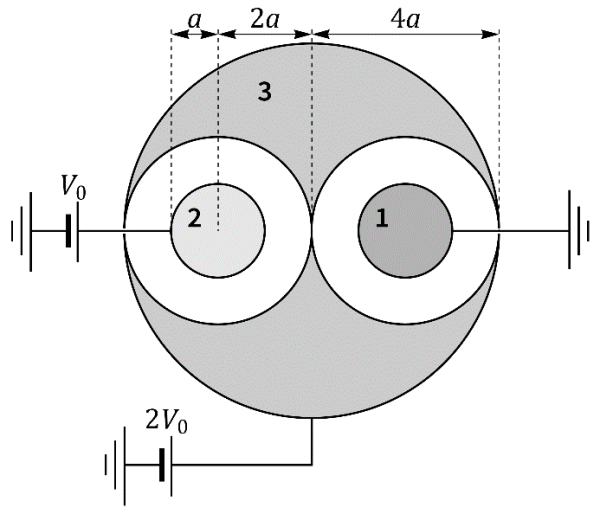
Se tiene un sistema formado por tres conductores metálicos. Dos de ellos (“1” y “2”) son esferas macizas de radio $a=9\,\mathrm {mm}$. El tercero es una esfera de radio $c=4a=36\,\mathrm {mm}$, que tiene dos huecos esféricos de radio $b=2a=18\,\mathrm {mm}$ en cuyo interior se encuentran los conductores “1” y “2”, concéntricamente a cada hueco. El conductor “1” se encuentra conectado a tierra, el “2” a una fuente de tensión de $V_{0}=+1\,\mathrm {kV}$, y el “3” a una de tensión $V_{3}=2V_{0}=2\,\mathrm {kV}$. El infinito se halla a potencial 0 (tierra). No hay más conductores en el sistema. Calcule

1. Las capacidades entre cada par de conductores y de cada uno con el infinito, si las hubiera.
2. La carga neta de cada uno de los 3 conductores.
3. La carga de cada una de las 5 superficies, tanto las exteriores de cada uno como las paredes de los huecos.
4. La energía electrostática almacenada en el sistema.

Solución

Tres superficies esféricas concéntricas

Se tiene un sistema formado por tres superficies conductoras esféricas concéntricas, de radios $2b$, $3b$ y $6b$. Inicialmente la esfera interior almacena una carga $-Q_{0}$, la intermedia está aislada y descargada y la exterior almacena una carga $+Q_{0}$.

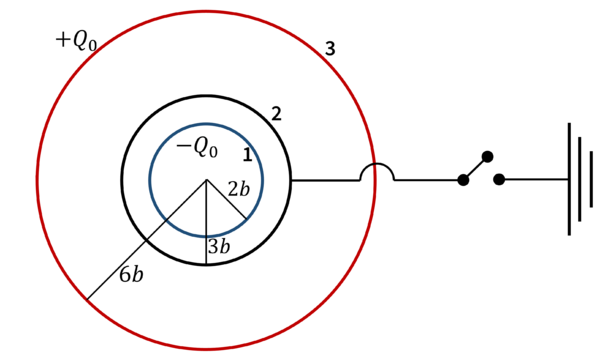
1. Calcule el potencial al que se encuentra cada esfera.
2. Halle el campo eléctrico en los puntos del eje OZ siguientes: $z=0$, $z=5b/2$, $z=4b$ y $z=8b$, siendo el origen de coordenadas el centro de las esferas.
3. Halle la energía almacenada en el sistema

En un momento dado se cierra el interruptor que conecta la esfera intermedia a tierra. Una vez que se alcanza de nuevo el equilibrio electrostático:

4. ¿Cuáles son las nuevas cargas y potenciales de los tres conductores?
5. ¿Cuánto vale ahora el campo eléctrico en los puntos del apartado 2?
6. ¿Cuánto vale la energía almacenada en el sistema?
7. ¿Cuánta energía se ha perdido en el proceso?

Solución