Triángulo de esferas conductoras

Enunciado

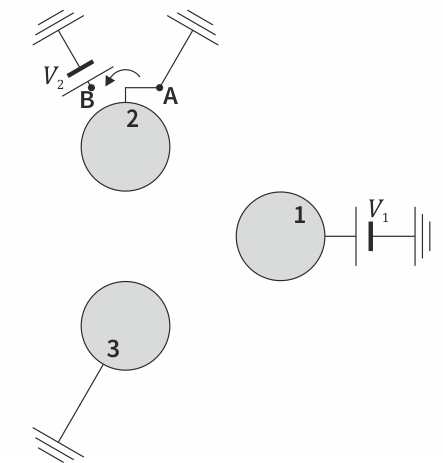
Un sistema de conductores está formado por tres esferas metálicas idénticas de radio b, situadas en los vértices de un triángulo equilátero de lado a ($a>2b$). No hay más conductores ni cargas en el sistema.

Se encuentra experimentalmente que cuando la esfera “1” se encuentra a 10 kV y la “2” y la “3” a tierra, la carga de la propia esfera “1” es de +8 nC, mientras que la de la “2” es de −3 nC.

1. Calcule la energía eléctrica almacenada en el sistema.
2. Dibuje el circuito equivalente y calcule las capacidades de sus condensadores.

Suponga que, sin tocar las esferas 1 y 3, se pasa el interruptor de la esfera 2 a la posición B, de manera que su voltaje pasa a ser de 5kV. Una vez que se llega al equilibrio:

3. ¿Cuál es la nueva carga de cada esfera?
4. ¿Y la energía almacenada?
5. ¿Qué trabajo realiza en el proceso el generador conectado a la esfera 1 y el conectado a la esfera 2?

Energía almacenada

Inicialmente no conocemos la carga del conductor “3” (aunque es fácil de deducir), pero no la necesitamos, porque su voltaje es nulo. La energía almacenada es

$U_{\mathrm {e} }={\frac {1}{2}}Q_{1}V_{1}+{\frac {1}{2}}Q_{2}V_{2}+{\frac {1}{2}}Q_{3}V_{3}={\frac {1}{2}}(8\,\mathrm {nC} )(10\,\mathrm {kV} )+{\frac {1}{2}}(-3\,\mathrm {nC} )\cdot 0+{\frac {1}{2}}Q_{3}\cdot 0=40\,\mu \mathrm {J}$

Circuito equivalente

Un sistema de conductores se puede modelar por un sistema de condensadores.

Entre cada para de conductores se stúa un condensador que representa las partes de cada uno que están en influencia total. En este caso, por la simetría del sistema, las capacidades entre cada par de condensadores son idénticas. Llamemos $C_{a}$ a esta capacidad.

Además de estos, se añaden en el modelo otros condensadores que representan la parte de cada conductor que está en influencia con el infinito, que está a tierra. De nuevo, por la simetría del sistema, estos tres condensadores son iguales. Llamemos $C_{b}$ a sus capacidades.

Para completar el circuito, se añaden las fuentes de tensión y los interruptores. Con esto nos queda el circuito de la figura:

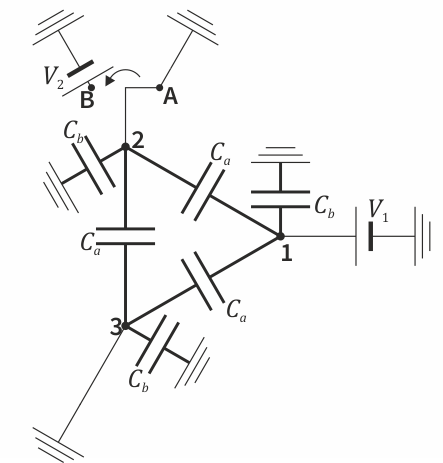
Para hallar las capacidades de los condensadores, usamos los datos de las cargas y potenciales que nos da el enunciado.

En el circuito, la carga del conductor $1$ es la suma de las cargas de las placas conectadas al nodo “1”. Puesto que la carga en una placa es el producto de la capacidad por la diferencia de potencial entre esa laca y la otra nos queda

$Q_{1}=C_{a}(V_{1}-V_{2})+C_{a}(V_{1}-V_{3})+C_{b}(V_{1}-0)\,$

Si medimos la carga en nC y el voltaje en kV, la capacidad nos resulta en pF. Poniendo valores numéricos nos queda

$+8=C_{a}(10)+C_{a})10+C_{b}(10)=20C_{a}+10C_{b}\,$

Operamos de la misma manera para la esfera "2"

$Q_{2}=C_{a}(V_{2}-V_{1})+C_{a}(V_{2}-V_{3})+C_{b}(V_{2}-0)\,$ $-3=C_{a}(-10)+C_{a}(0)+C_{b}(0)=-10C_{a}$

lo que nos da la capacidad $C_{a}$

$C_{a}={\frac {3}{10}}\mathrm {pF} =0.3\,\mathrm {pF}$

y, sustituyendo en la ecuación anterior,

$8=20\cdot 0.3+10C_{b}$

obtenemos

$C_{b}=0.2\,\mathrm {pF}$

Nuevo estado de equilibrio

Una vez conectada la segunda fuente, obtenemos las nuevas cargas empleando el circuito equivalente (que no cambia por el hecho de que se modifiquen los voltajes o cargas). Tenemos, para el conductor “1”.

$Q_{1}=C_{a}(V_{1}-V_{2})+C_{a}(V_{1}-V_{3})+C_{b}(V_{1}-0)=0.3(10-5)+0.3(10-0)+0.2(10-0)=+6.5\,\mathrm {nC}$

Para el conductor 2

$Q_{2}=C_{a}(V_{2}-V_{1})+C_{a}(V_{2}-V_{3})+C_{b}(V_{2}-0)=0.3(5-10)+0.3(5-0)+0.2(5-0)=+1.0\,\mathrm {nC}$

y para el conductor 3

$Q_{3}=C_{a}(V_{3}-V_{1})+C_{a}(V_{3}-V_{2})+C_{b}(V_{3}-0)=0.3(0-10)+0.3(0-5)+0.2(0-0)=-4.5\,\mathrm {nC}$

Nueva energía almacenada

Empleamos de nuevo la fórmula para la energía de un sistema de conductores

$U_{\mathrm {e} }={\frac {1}{2}}Q_{1}V_{1}+{\frac {1}{2}}Q_{2}V_{2}+{\frac {1}{2}}Q_{3}V_{3}={\frac {1}{2}}(6.5\,\mathrm {nC} )(10\,\mathrm {kV} )+{\frac {1}{2}}(1\,\mathrm {nC} )\cdot 5+{\frac {1}{2}}(-4.5)\cdot 0=35\,\mu \mathrm {J}$

Trabajo de los generadores

Cada generador realiza un trabajo igual a la carga que pasa por él multiplicada por la diferencia de potencial a que la somete. Para el 1

$W_{1}=V_{1}\,\Delta Q_{1}=10(6.5-8.0)=-15\,\mu \mathrm {J}$

y para el 2

$W_{2}=V_{2}\,\Delta Q_{2}=5(1-(-3))=20\,\mu \mathrm {J}$