Se tiene una esfera metálica maciza de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle a}
y no hay más conductores ni cargas en el sistema. Si la esfera almacena una carga total Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q}
calcule:
el potencial y el campo eléctrico en todos los puntos del espacio.
el voltaje al que se encuentra
la densidad superficial de carga.
la energía electrostática que almacena.
Particularice los resultados anteriores para un radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle a = 10\,\mathrm{cm}}
y una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q= 36\,\mathrm{nC}}
.
Suponga ahora que lo que se conoce inicialmente su voltaje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0}
, pero no su carga. Halle en ese caso la carga que almacena, así como el resto de las cantidades obtenidas anteriormente. Particularice los resultados anteriores para un voltaje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0 = 1.8\,\mathrm{kV}}
.
Potencial y campo eléctrico
Una de las herramientas básica en el estudio del problema del potencial eléctrico es el “teorema de existencia y unicidad” que nos dice que la distribución de potencial en un conjunto de conductores en equilibrio electrostático existe y es única. Esto quiere decir que podemos hallarla por cualquier método, incluida la inspiración. Si cumple las condiciones del problema, es la solución, porque no hay otra.
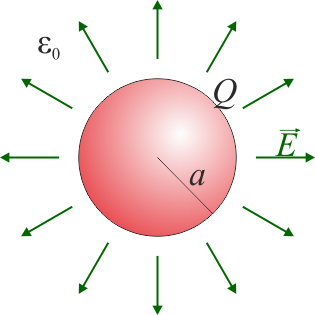
En este problema tenemos un conductor esférico que almacena una carga Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q}
. De este sistema sabemos que:
El potencial en todos los puntos de la esfera es el mismo, aunque no sabemos cuanto vale
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V= V_0 \qquad (r < a)}
La carga total de la esfera es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q}
, lo que implica, para cualquier superficie que la rodee
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_0 \oint \vec{E}\cdot\mathrm{d}\vec{S}= Q}
Lejos de la esfera el potencial eléctrico se anula
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V \to 0\qquad (r\to\infty)}
No hay más conductores ni cargas en el sistema.
En principio no podemos suponer que la carga se distribuye uniformemente por la superficie del conductor. Ese no es un dato del problema.
Tal como se ve en la solución de ese problema, el potencial de esa esfera vale
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V(r)=\begin{cases} \displaystyle \frac{Q}{4\pi\varepsilon_0a} & r \leq a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r > a \end{cases}}
y por simple comprobación vemos que satisface todas las propiedades del sistema.
Por tanto, esta es la solución del problema.
El campo eléctrico, para este mismo sistema vale
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}=\begin{cases} \vec{0} & r < a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & r > a \end{cases}}
Voltaje de la esfera
El voltaje de la esfera es el correspondiente a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r < a}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0 = \frac{Q}{4\pi\varepsilon_0 a}}
o, equivalente, si lo que conocemos es el potencial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q = CV\qquad\qquad C = 4\pi\varepsilon_0a}
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C}
la capacidad de un conductor esférico.
Densidad superficial de carga
Puesto que la carga resulta estar distribuida uniformemente, la densidad vale
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sigma_s = \frac{Q}{4\pi a^2}}
En la superficie de la esfera, por ser esta conductora, se cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}(r=a^+)=\frac{Q}{4\pi\varepsilon_0 a^2}\vec{u}_r = \frac{Q/4\pi a^2}{\varepsilon_0}\vec{u}_r=\frac{\sigma_s}{\varepsilon_0}\vec{n}}
El campo en la superficie se relaciona con el potencial al que se encuentra ésta, sustituyendo la relación entre la carga y el potencial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}(r=a^+)=\frac{Q}{4\pi\varepsilon_0 a^2}\vec{u}_r = \frac{4\pi\varepsilon_0a V}{4\pi\varepsilon_0 a^2}\vec{u}_r = \frac{V}{a}\vec{u}_r}
Energía electrostática
La energía electrostática almacenada en un sistema de conductores puede hallarse mediante la fórmula
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_\mathrm{e}=\frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2+\cdots}
En este caso, que tenemos un solo conductor, esta suma se reduce a un solo término
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_\mathrm{e}= \frac{1}{2}QV_0}
Sustituyendo el valor del potencial de la esfera queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_\mathrm{e}=\frac{1}{2}\,\frac{Q^2}{4\pi\varepsilon_0a}}
Valores numéricos
Sustituyendo los datos del enunciado
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q = 36\,\mathrm{nC}\qquad a = 10\,\mathrm{cm}}
obtenemos el voltaje de la esfera
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V = \frac{Q}{4\pi\varepsilon_0 a}=9\times 10^9\times \frac{36\times 10^{-9}}{10^{-1}}\,\mathrm{V}=3.24\,\mathrm{kV}}
la densidad de carga superficial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sigma_s = \frac{Q}{4\pi a^2}=2.86\times 10^{-7}\,\frac{\mathrm{C}}{\mathrm{m}^2}}
y la energía almacenada
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_\mathrm{e}=\frac{1}{2}QV = 58.32\,\mu\mathrm{J}}
Caso de voltaje conocido
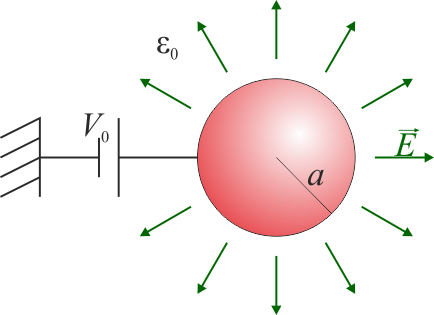
Si el dato que nos dan es el voltaje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0}
tenemos que el problema es exactamente el mismo, solo que ahora sabemos el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V}
, pero ignoramos el de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q}
. Por tanto, no necesitamos volver a resolver el problema. Nos basta con emplear la solución que acabamos de dar, buscando previamente el valor de la carga que nos da Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0}
. Del potencial en el conductor tenemos que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V_0=\frac{Q}{4\pi\varepsilon_0a}\qquad \Rightarrow\qquad Q = 4\pi\varepsilon_0 a V_0}
y ahora con este valor de la carga, simplemente sustituimos en las expresiones anteriores.
Potencial en todo el espacio
Queda, sustituyendo,
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle V(r)=\begin{cases} \displaystyle V_0 & r \leq a \\ & \\ \displaystyle\frac{V_0a}{r} & r > a \end{cases}}
Campo eléctrico en todo el espacio
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}=\begin{cases} \vec{0} & r < a \\ & \\ \displaystyle\frac{V_0a}{r^2}\vec{u}_r & r > R \end{cases}}
Densidad de carga superficial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sigma_s = \frac{\varepsilon_0 V_0}{a}}
Dividiendo por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \varepsilon_0}
queda el campo en la superficie de la esfera.
Energía almacenada
Ahora, en lugar de sustituir el potencial, sustituimos la carga
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_\mathrm{e}=\frac{1}{2}QV_0=\frac{1}{2}4\pi\varepsilon_0a V_0^2}
Siendo los valores numéricos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q = 4\pi\varepsilon_0 a V_0 = 2.0\,\mathrm{nC}}Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sigma_s = 0.159\,\frac{\mu\mathrm{C}}{\mathrm{m}^2}}Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U_e = 18\,\mu\mathrm{J}}
