Energía en la carga de un conductor

Energía en la carga de un condensador

Un determinado sistema está formado exclusivamente por un conductor de capacidad C. Inicialmente este conductor almacena una carga $Q_{A}$. Una fuente de tensión continua $V_{B}$ se conecta al conductor mediante un interruptor que se cierra bruscamente.

1. ¿Cuánto cambia la carga almacenada en el conductor?
2. ¿Cuánto cambia la energía electrostática del sistema?
3. ¿Qué trabajo realiza la fuente en este proceso? ¿Cuánta energía se disipa?

Carga almacenada

Inicialmente tenemos una craga almacenada $Q_{A}$. Tras la conexión de la fuente, el voltaje del conductor pasa a ser $V_{B}$ y la carga del condensador que forma con el infinito este

$Q_{B}=C(V_{B}-0)=CV_{B}$

con lo que la variación de la carga almacenada es

$\Delta Q=Q_{B}-Q_{A}=CV_{B}-Q_{A}\,$

Energía almacenada

Antes de la consexión la energía es

$U_{mathrm{e}A}={\frac {Q_{A}^{2}}{2C}}$

y tras la conexión

$U_{mathrm{e}B}={\frac {CV_{B}^{2}}{2}}$

siendo la diferencia

$\Delta U_{\mathrm {e} }={\frac {CV_{B}^{2}}{2}}-{\frac {Q_{A}^{2}}{2C}}={\frac {(CV_{B})^{2}-Q_{A}^{2}}{2}}$

Vemos que esta energía no cambia cuando $V_{B}=Q_{A}/C$, es decir, cuando el conductor ya estaba a potencial $V_{B}$. También se anula si $CV_{B}=-Q_{A}$, es decir, cuando la carga cambia de signo.

Trabajo realizado por el generador

Una fuente de tensión de corriente continua fija en todo momento la misma diferencia de potencial. En este caso $V_{B}$. Para ello, pone o quita carga en el conductor al que está conectada. El trabajo que realiza es igual al producto de la carga que pasa por él, multiplicada por la diferencia de potencial que suministra

$W_{\mathrm {gen} }=V_{B}\,\Delta Q=V_{B}(CV_{B}-Q_{A})=CV_{B}^{2}-Q_{A}V_{B}$

Vemos que el trabajo se anula cuando el potencial inicial ya es $V_{B}$ (porque entonces no hace nada, ni pone ni quita carga) y también cuando $V_{B}=0$, ya que en ese caso no hay generador, solo una conexión a tierra.

Energía disipada

El trabajo que realiza el generador (que es de entrada en el sistema) no coincide con la variación en la energía eléctrica almacenada. La razón es que hay disipación de energía, bien en forma de aumento de la temperatura (incremento en la energía interna), bien en la producción de calor. Identificando ambos efectos como calor tenemos que

$W_{\mathrm {in} }=\Delta U_{\mathrm {e} }+Q_{\mathrm {out} }$

lo que nos da

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q_\mathrm{out}=W_\mathrm{gen}-\Delta U_\mathrm{e}=CV_B^2-Q_AV_B-\frac{CV_B^2}{2}+\frac{Q_A^2}{2C}= \frac{CV_B^2}{2}-Q_AV_B+\frac{Q_A^2}{2C}}

Esta cantidad essiempre positiva, ya que se puede poner como un cuadrado perfecto.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q_\mathrm{out}=\frac{(CV_B-Q_A)^2}{2C}}

Este calor solo se anula cuando el voltaje inicial del conductor coincide con su voltaje final.

Representación gráfica

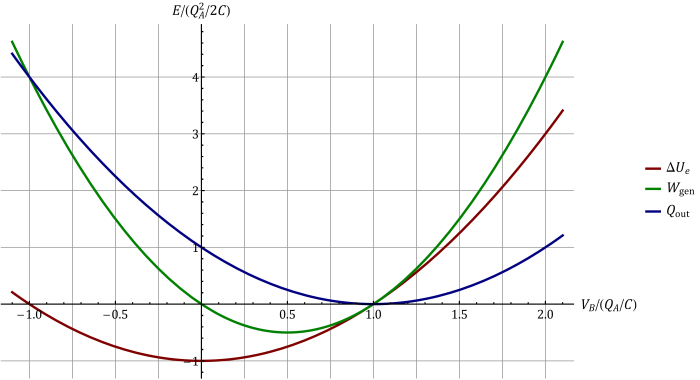
Podemos trazar las gráficas de las tres cantidades como función del voltaje aplicado por la fuente.

Resultan tres parábolas. Podemos ver que si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q_A=CV_B} se anulan las tres, ya que no ocurre nada en el sistema.

También podemos representarlas como función de la carga inicial, para un voltaje fijado de la fuente. En este caso resultan dos parábolas y una recta.

Podemos ver que cuando la carga inicial del conductor es nula, la fuente realiza un trabajo que es exactamente el doble de lo que aumenta la carga almacenada y que la mitad de ese trabajo se va en calor.

Caso de una fuente de tensión variable

Imaginemos que la fuente de tensión no aplica siempre el mismo voltaje, sino que este va variando gradualmente desde su valor inicial al valor final. Tenemos aquí lo que en termodinámica es un proceso cuasiestático.

El procedimiento no afecta a la energía almacenada. Su valor inicial y su valor final son los mismos que en el caso anterior ya

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta U_\mathrm{e}=\frac{1}{2}CV_B^2-\frac{Q_A^2}{2C}}

El trabajo que realiza el generador sí es diferente. Ahora el voltaje comienza valiendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle V_A=Q_A/C} y de ahí cambia hasta un valor Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle V_B} . En medio va pasando por todos los valores de V. El trabajo que realiza corresponde a la cantidad de carga que pasa cuando está a ese voltaje

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W_\mathrm{gen}=V\,\mathrm{d}Q}

y, por tanto,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W_\mathrm{gen}=\int_A^B V\,\mathrm{d}Q}

La ecuación de estado es muy simple en este caso: la carga del conductor es proporcional a su voltaje y, por tanto,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q=CV\qquad\Rightarrow\qquad \mathrm{d}Q=C\,\mathrm{d}V}

lo que nos da el trabajo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W_\mathrm{gen}=C\int_{V_A}^{V_B} V\,\mathrm{d}V = \frac{CV_B^2}{2}-\frac{CV_A^2}{2}}

Sustituimos el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle V_A} y queda

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W_\mathrm{gen}=\frac{1}{2}CV_B^2-\frac{Q_A^2}{2C}}

Este trabajo sí coincide con la variación de energía eléctrica. Por tanto, en este proceso cuasiestático no se genera calor.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Q_\mathrm{out}=W_\mathrm{in}-\Delta U=0}