Problemas de introducción a la termodinámica (GIOI)

Conversión entre escalas de temperaturas

Exprese las siguientes temperaturas en la escala Celsius, absoluta y Fahrenheit:

1. Cero absoluto
2. 0°F
3. 100°F
4. Punto triple del agua
5. Punto de fusión del azufre a 1 atm
6. Punto de sublimación del hielo seco a 1 atm

Solución

Nueva escala de temperatura

Zorg, un habitante de Titán, construye una escala de temperaturas basada en el metano tal que a la fusión (91 K) le corresponden 0 °Z y a la ebullición (116 K) 100 °Z. ¿Cuál es la temperatura del cero absoluto en esta escala?

Solución

Fahrenheit 451

El título de la novela de Ray Bradbury “Fahrenheit 451” se refiere a la temperatura a la que arde el papel. Si 32°F son 0℃ y 212 °F son 100℃, ¿cómo se titularía esta novela en la escala absoluta?

Solución

Aire en una habitación

Estime la masa de aire en el aula 310 de la ETSI (a) Un día de enero a las 5 de la madrugada. (b) Un día de julio a las 4 de la tarde. Razone las aproximaciones efectuadas.

Solución

Dilatación de una esfera metálica

Se tiene una bola hueca de hierro que a 20°C tiene un radio interior de 12.0 mm y un radio exterior de 15.0 mm, siendo la densidad del hierro a esta temperatura 7874 kg/m³ y su coeficiente de dilatación lineal 11.8×10⁻⁶K⁻¹.

Se eleva la temperatura de la bola a 50°C. Determine:

1. Los nuevos radios interior y exterior de la bola.
2. El incremento en el volumen ocupado por el hierro.
3. La variación en la densidad del hierro

Solución

Dilatación de raíles

Los raíles ferroviarios son de acero y tienen 18 m de longitud a 20°C. Si deben operar entre -10°C y 60°, ¿qué espacio debe dejarse como mínimo entre un tramo y el siguiente si se tienden a una temperatura de 20°?

Dato: Coeficiente de dilatación lineal del acero: 13×10⁻⁶K⁻¹

Solución

Dilatación de tapa

Una forma de abrir un bote de vidrio cuya tapa metálica está demasiado apretada consiste en sumergirlo en un baño de agua caliente. Si sumergimos en agua a 60 °C un bote de 4.0 cm de radio con tapa de estaño que a 20 °C encaja perfectamente y el coeficiente de dilatación lineal del vidrio es $9\times 10^{-6}\mathrm {K} ^{-1}$ y el del estaño es $23\times 10^{-6}\mathrm {K} ^{-1}$, ¿cuánta holgura queda al calentarlo?

Solución

Cálculo de coeficientes

La densidad del agua, en kg/m³, para valores próximos a una presión de 15.0 MPa y una temperatura de 300℃ (estado del agua en una central nuclear) viene dada por la siguiente tabla:

ρ (kg/m³)	T = 300 ℃	T = 301 ℃
p = 15.0 MPa	725.55	723.46
p = 15.1 MPa	725.75	723.66

1. ¿Cuánto vale, aproximadamente, el coeficiente de dilatación volumétrica, β, a 300℃ y 15.0 MPa?
2. ¿Cuánto vale, aproximadamente, el coeficiente de compresibilidad, $\kappa _{T}$, a 300℃ y 15.0 MPa?

Solución

Compresión de un gas por una pesa

Un cilindro vertical de sección cuadrada (esto es, un prisma) de 4.0 cm de lado contiene hidrógeno a 27°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Se coloca sobre la tapa una pesa de 40 N. Halle la altura de la tapa una vez que se alcanza de nuevo el equilibrio térmico con el exterior. ¿A qué temperatura habrá que calentar el gas para que la tapa vuelva a su posición inicial, con el peso todavía encima?

Solución

Termómetro con dos cámaras de gas

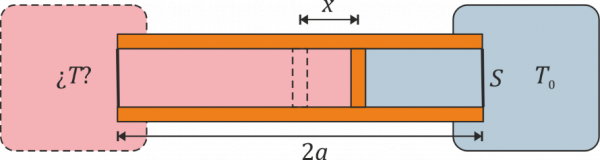
Se construye un termómetro de gas ideal según el siguiente principio: un tubo cilíndrico de sección $S$ y longitud $2a$ con paredes adiabáticas y bases diatermas es dividido por un pistón, también adiabático, que puede deslizarse sin rozamiento por el interior del tubo. En el interior de las dos cámaras se encuentra un gas ideal. Una de las dos cámaras se mantiene en contacto térmico con un foco a temperatura $T_{0}$, mientras que la otra se pone en contacto con el sistema cuya temperatura se quiere medir. Cuando las dos temperaturas son iguales el pistón se encuentra en la posición central y la presión del gas es $p_{0}$.

1. Calcule la temperatura absoluta $T$ a la que se encuentra el sistema cuando el pistón se ha desplazado una cantidad $x$ desde el centro hacia el sistema a $T_{0}$. ¿Resulta una escala lineal de temperaturas? ¿A cuánto tiende $x$ si $T\to 0$ o si $T\to \infty$?
2. Supongamos que el tubo mide 20 cm, la temperatura de referencia es $T_{0}=300\,\mathrm {K}$ y el pistón se desplaza 1 cm. ¿Cuál es la temperatura del sistema exterior?

Solución

Equivalencia de un psi

Una atmósfera equivale a 101325 Pa. Un psi es la presión ejercida por una libra (4.448 N) sobre un cuadrado de lado 1 pulgada (2.54 cm). ¿A cuántos psi equivale una atmósfera?

Solución

Equivalencia de una atmósfera técnica

Una atmósfera técnica (at) es la presión ejercida por el peso de un kilogramo sobre una superficie de 1 cm². ¿A cuántos pascales equivale 1 at? ¿Y cuántas atmósferas estándar, atm? ¿Y cuantos psi?

Solución

Tubo con cámaras con hidrógeno y nitrógeno

Se tiene una cámara cilíndrica horizontal de 100 cm² de sección y 60 cm de longitud de paredes rígidas no aisladas térmicamente. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 2.8 g de H₂ gaseoso y en la de la derecha 2.8 g de N₂. Los dos gases y el ambiente que los rodea están a 27°C.

1. Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central.
2. Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas

Solución

Dos cámaras inicialmente aisladas

Dos cámaras A y B con el mismo volumen de aire están separadas por un émbolo que puede moverse libremente. Las paredes y el émbolo están aislados térmicamente. Inicialmente las dos cámaras están en equilibrio. Se retira el aislante del émbolo. Una vez que se vuelve a alcanzar el equilibrio, el volumen de A es el doble que el de B.

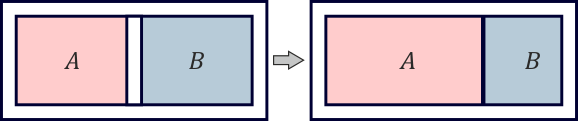
1. Antes de que se retirara el aislante, ¿qué proporción había entre las temperaturas de A y B?
2. Una vez que se ha alcanzado de nuevo el equilibrio, ¿qué proporción hay entre las densidades de masa del aire de ambas cámaras?