Problemas de cinemática del sólido rígido (CMR)

Problemas del boletín

Velocidad instantánea en tres puntos

En un determinado instante, tres puntos de un sólido rígido en movimiento ocupan las posiciones dadas por

$O(0,0,0);\qquad A(0,a,0);\qquad B(0,0,2a).$

Las velocidades instantáneas de esos puntos, medidas en el mismo sistema de referencia son:

${\vec {v}}^{O}=v_{0}\,{\vec {\imath }};\qquad {\vec {v}}^{A}={\dfrac {v_{0}}{2}}\,{\vec {k}};\qquad {\vec {v}}^{B}=v_{0}\,({\vec {\imath }}-{\vec {\jmath }}).$

1. Calcula la reducción cinemática en el punto $O$ de dicho movimiento instantáneo y averigua de qué tipo de movimiento se trata.
2. Calcula el vector velocidad instantánea de los puntos con velocidad mínima.
3. Obtén las expresión vectorial del lugar geométrico formado por los puntos con velocidad mínima.

Ejemplos de reducciones cinemáticas

Encuentra las reducciones cinemáticas instantáneas pedidas de cada uno de estos movimientos

1. Una rueda de radio $R$ que gira con velocidad angular constante $\omega$ alrededor de un eje perpendicular a ella que pasa por su centro. Encuentra la reducción canónica.
2. Una rueda de radio $R$ rueda sin deslizar sobre una superficie horizontal de modo que su centro avanza con velocidad uniforme $v_{0}$. Encuentra la reducción en el centro y la reducción canónica.
3. Una rueda de radio $R$ rueda y desliza con velocidad angular $\omega$ alrededor de un eje perpendicular a ella, de modo que el punto de contacto con el suelo tiene una vez relativa a éste de módulo $v_{des}$. Encuentra la reducción en el punto de contacto y la reducción canónica.
4. Un tornillo gira con velocidad angular uniforme $\omega$ y avanza con velocidad uniforme $v$ paralelamente a su eje. Encuentra la reducción en el punto más alto de la superficie frontal del tornillo y la reducción canónica.

Disco desenrollándose de una cuerda

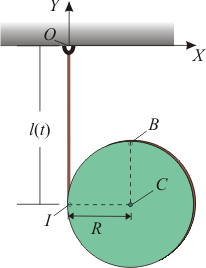
Un disco de radio $R$ gira y cae, siempre contenido en el plano vertical $OXY$, mientras se desenrrolla de una cuerda que pende verticalmente, y cuya longitud aumenta según la ley horaria $l(t)=R+K\!\ t^{2}$ (donde $K$ es una constante conocida).

1. Obtenga la reducción cinemática que describe el movimiento instantáneo del disco.
2. Velocidad y aceleración instantáneas del punto $B$ indicado en la figura.

Otros problemas

Traslación y rotación en el plano

En un movimiento plano, un sólido realiza una traslación $8{\vec {\imath }}+6{\vec {\jmath }}$ seguida de una rotación de 90° en torno a la nueva posición del origen de coordenadas. ¿Qué punto del plano está al final en la misma posición que al principio? ¿Cómo cambia el resultado si la rotación que sucede a la traslación es de un ángulo θ tal que tg⁡(θ)=3\/4?

Caso de rotación finita

Tras una determinada rotación en torno al origen de coordenadas la base ligada al sólido se expresa en función de la base fija como

${\begin{array}{rcl}{\vec {\imath }}_{2}&=&0.60{\vec {\imath }}_{1}+0.64{\vec {\jmath }}_{1}-0.48{\vec {k}}_{1}\\{\vec {\jmath }}_{2}&=&0.60{\vec {\jmath }}_{1}+0.80{\vec {k}}_{1}\\{\vec {k}}_{2}&=&0.80{\vec {\imath }}_{1}-0.48{\vec {\jmath }}_{1}+0.368{\vec {k}}_{1}\end{array}}$

1. Compruébese que la base es ortonormal.
2. Determine un vector en la dirección del eje de rotación.
3. Calcule el ángulo girado en torno a este eje (estudie el cambio de un vector perpendicular al eje).

Clasificación de movimientos de un sólido

Se tiene un sólido formado por ocho masas iguales, $m=100\,\mathrm {g}$, situadas en los vértices de un cubo de lado $b=10\,\mathrm {cm}$. En un instante dado, una de ellas se encuentra en el origen de coordenadas y las aristas son paralelas a los ejes de coordenadas.

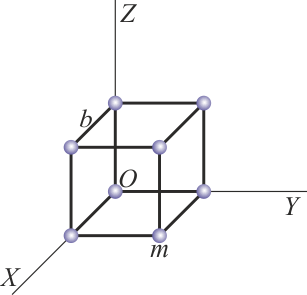
Considere los casos siguientes para las velocidades de las masas situadas en ${\vec {r}}_{1}=b{\vec {\imath }}$, ${\vec {r}}_{2}=b{\vec {\jmath }}$ y ${\vec {r}}_{3}=b{\vec {k}}$

Caso	${\vec {v}}_{1}$ (cm/s)	${\vec {v}}_{2}$ (cm/s)	${\vec {v}}_{3}$ (cm/s)
I	${\vec {\jmath }}-{\vec {k}}$	$-{\vec {\imath }}+{\vec {k}}$	${\vec {\imath }}-{\vec {\jmath }}$
II	${\vec {\imath }}+{\vec {\jmath }}-{\vec {k}}$	${\vec {k}}$	$2{\vec {\imath }}-{\vec {\jmath }}$
III	${\vec {\jmath }}-{\vec {k}}$	$-{\vec {\imath }}+{\vec {k}}$	${\vec {\imath }}-{\vec {\jmath }}+{\vec {k}}$
IV	${\vec {\imath }}-{\vec {\jmath }}$	${\vec {\imath }}-{\vec {\jmath }}$	${\vec {\imath }}-{\vec {\jmath }}$
V	${\vec {\imath }}+2{\vec {\jmath }}$	${\vec {\jmath }}+2{\vec {k}}$	$2{\vec {\imath }}+{\vec {k}}$
VI	${\vec {\imath }}+{\vec {\jmath }}+{\vec {k}}$	${\vec {\imath }}+{\vec {\jmath }}+{\vec {k}}$	${\vec {0}}$

1. Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez.
2. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
3. Para las rotaciones y movimientos helicoidales, determine la posición del EIR o EIRMD.
4. Para los movimientos compatibles, calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.

Rodadura y deslizamiento de un disco

Un disco de radio $R$ y masa $M$ rueda y desliza sobre el plano horizontal $y=0$ de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B son de la forma

${\vec {v}}_{A}=v_{A}{\vec {\imath }}\qquad {\vec {v}}_{B}=v_{B}{\vec {\imath }}$

1. Calcule la velocidad angular del disco.
2. Halle la velocidad del centro del disco, C, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
3. Determine la posición del centro instantáneo de rotación.
4. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
   1. $v_{A}=-v_{B}$
   2. $v_{A}=0$
   3. $v_{A}=v_{B}$

Velocidades y aceleraciones en un disco rodante sobre un plano

Un disco de radio $R$ rueda sin deslizamiento sobre el plano horizontal $y=0$ de forma que la posición de su centro sigue una ley

${\overrightarrow {OG}}=x{\vec {\imath }}+R{\vec {\jmath }}$

En función de x y sus derivadas temporales ${\dot {x}}$ y ${\ddot {x}}$ halle

1. La velocidad angular del disco.
2. La velocidad del punto B situado diametralmente opuesto al de contacto con el suelo, A, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
3. La aceleración angular del disco
4. Las aceleraciones de los puntos A, B, D y E.

Diferentes movimientos de una esfera

Considérese una esfera de masa $M$ y radio $R$ que se mueve sobre la superficie horizontal $z=0$. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

${\vec {v}}_{O}={\vec {0}}$

Para este mismo instante la velocidad de los puntos ${\vec {r}}_{A}=-R{\vec {\imath }}+R{\vec {k}}$ y ${\vec {r}}_{B}=+R{\vec {\imath }}+R{\vec {k}}$ situados en un diámetro horizontal valen respectivamente

${\vec {v}}_{A}=v_{A}{\vec {\jmath }}\qquad {\vec {v}}_{B}=v_{B}{\vec {\jmath }}$

Para los tres casos siguientes:

• $v_{A}=+v_{B}$
• $v_{A}=0$
• $v_{A}=-v_{B}$

1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
2. Calcule la velocidad angular del sólido.
3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

Deslizamiento de una barra

Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60 cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina

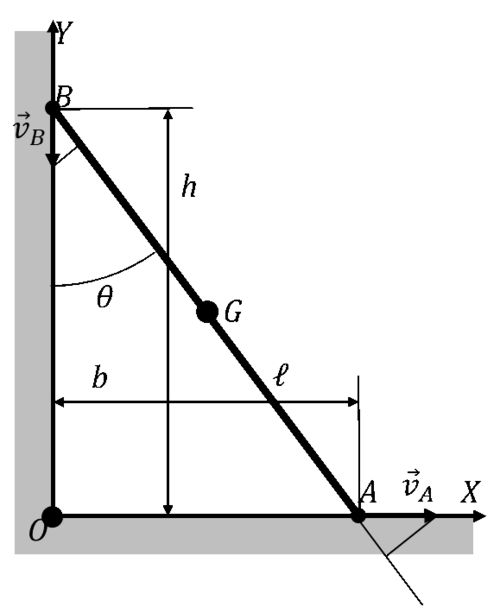
1. ¿Con qué velocidad se mueve el punto B, extremo superior de la barra?
2. Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OZ, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito?
3. Suponiendo un caso más general en el que la barra forma un ángulo θ con la pared y las derivadas de este ángulo respecto al tiempo valen ${\dot {\theta }}$ y ${\ddot {\theta }}$, siendo $\ell$ la longitud de la barra. Halle cuánto valen en ese caso
   1. Las velocidades y aceleraciones lineales de los puntos A y B de apoyo de la barra en el suelo y la pared, del centro G de la barra y de la esquina O considerada como punto del sólido.
   2. La posición del CIR, ¿qué curva describe al ir moviéndose la barra?
      1. En un sistema de referencia fijo unido al suelo y la pared.
      2. En un sistema de referencia móvil ligado a la barra.
4. Para cada instante, ¿hay algún punto que tenga aceleración nula? ¿Y aceleración normal nula? ¿Y aceleración tangencial nula?

${\displaystyle }$

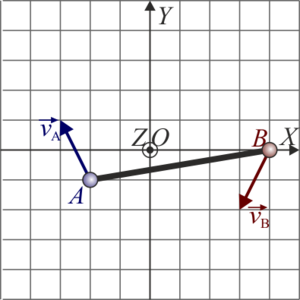
Ejemplo gráfico de movimiento plano

En un movimiento plano, se tiene que la velocidad instantánea de dos puntos A y B es la ilustrada en la figura (para la posición, la cuadrícula representa cm y para la velocidad cm/s)

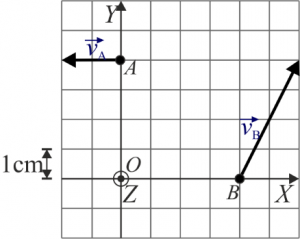
1. En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
2. ¿Dónde se encuentra el centro instantáneo de rotación?

Diferentes movimientos de una esfera

Considérese una esfera de masa $M$ y radio $R$ que se mueve sobre la superficie horizontal $z=0$. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

${\vec {v}}_{O}={\vec {0}}$

Para este mismo instante la velocidad de los puntos ${\vec {r}}_{A}=-R{\vec {\imath }}+R{\vec {k}}$ y ${\vec {r}}_{B}=+R{\vec {\imath }}+R{\vec {k}}$ situados en un diámetro horizontal valen respectivamente

${\vec {v}}_{A}=v_{A}{\vec {\jmath }}\qquad {\vec {v}}_{B}=v_{B}{\vec {\jmath }}$

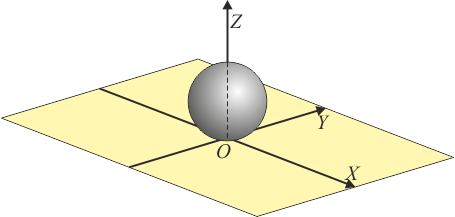
Para los tres casos siguientes:

• $v_{A}=+v_{B}$
• $v_{A}=0$
• $v_{A}=-v_{B}$

1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
2. Calcule la velocidad angular del sólido.
3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

Comparación de posibles movimientos

De las siguientes cuatro figuras, solo una representa velocidades posibles de los extremos A y B de una barra rígida que realiza un movimiento plano. ¿Cuál?

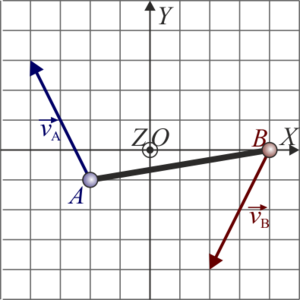
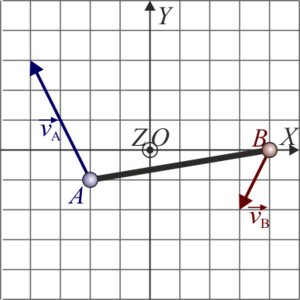
A	B
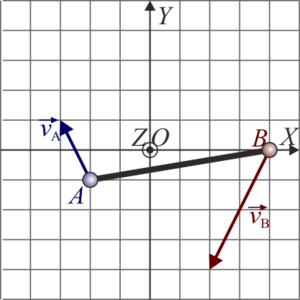
C	D

Para la barra anterior, ¿dónde se encuentra su centro instantáneo de rotación, según la cuadrícula de la figura?

¿Cuánto vale, en rad/s, la velocidad angular instantánea de este movimiento, si la cuadrícula representa m en distancias y m/s en velocidades?

Movimiento circular de sistema de referencia

Un sólido describe un movimiento plano tal que un punto A describe un movimiento circular de radio b alrededor del origen de coordenadas, con una ley $\phi =\phi (t)$. Simultáneamente, unos ejes ligados al sólido en el punto A van girando con una ley θ(t). Para cada instante, determine

1. la velocidad y aceleración del origen de coordenadas O considerado como parte del sólido.
2. la posición del CIR en función de θ, φ y sus derivadas respecto al tiempo.

Peonza rodante

Una peonza está formada por una varilla de longitud $\ell =20\,cm$ ensartada en un disco de radio $R=15\,\mathrm {cm}$. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez $v_{0}=48\,\mathrm {cm} /\mathrm {s}$. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula.

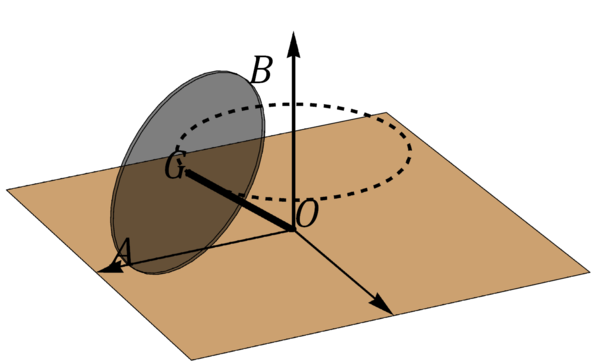
Para este movimiento, determine, en el instante en que A se encuentra sobre el eje OX:

1. La velocidad angular del sólido.
2. La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en $25{\vec {k}}\,\mathrm {cm}$, considerado como punto del sólido.
3. La aceleración angular del sólido.
4. La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.

Triángulo en movimiento helicoidal

El triángulo de vértices $A$, $B$, y $C$ constituye un sólido rígido en movimiento respecto al sistema de referencia fijo $OXYZ$. De dicho movimiento se conocen los siguientes datos:

1. Los vértices $A$ y $B$ permanecen en todo instante sobre el eje $OZ$, desplazándose ambos con igual velocidad instantánea ${\vec {v}}^{A}={\vec {v}}^{B}=v(t)\,{\vec {k}}$.
2. El vértice $C$ se mueve describiendo la hélice $\Gamma$, que en el sistema $OXYZ$ está descrita por las ecuaciones paramétricas:

$\Gamma :{\vec {r}}={\vec {r}}(\theta )\left\{{\begin{array}{l}x(\theta )=R\,\cos \theta \\y(\theta )=R\,\,\mathrm {sen} \,\theta \\z(\theta )=h\,\theta \\\end{array}}\right.$

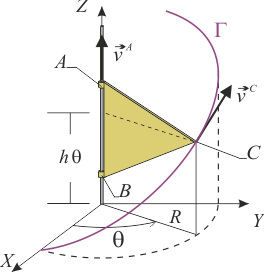
donde $R$ y $h$ son constantes conocidas. Se pide:

1. Indicar de forma razonada cual es el eje instantáneo de rotación y mínimo deslizamiento en este movimiento. Determinar el vector rotación total en términos de los datos expresados en el enunciado.
2. Expresar la componente normal de la aceleración del vértice $C$ en un instante cualquiera, en función de los datos del enunciado.
3. Para el caso en que $v(t)=v_{0}$ (cte), y $h=R/2$, calcular la aceleración del vértice $C$. Determinar la ley horaria $s=s(t)$ con que el punto $C$ describe su trayectoria.

Propiedades cinemáticas instantáneas de pieza triangular

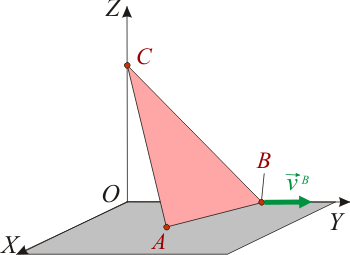
Una pieza triangular $ABC$ se mueve respecto de un sistema de referencia $OXYZ$, comportándose como un sólido rígido. Los vértices $C$ y $B$ de la pieza van recorriendo los ejes $OZ$ y $OY$, respecti-vamente, mientras que el vértice $A$ se desplaza siempre contenido en el plano $OXY$. En un determinado instante, cuando los vértices ocupan las posiciones de coordenadas

$A(a,a,0)\mathrm {;} \quad B(0,2a,0)\mathrm {;} \quad C(0,0,2a)$

la velocidad instantánea del vértice $B$ es ${\vec {v}}^{B}=v_{0}\!\ {\vec {\jmath }}$. Determine, para dicho instante de tiempo:

1. Velocidad del vértice $A$ y vector rotación instantánea.
2. Eje instantáneo de rotación y mínimo deslizamiento.
3. Derivada instantánea del vector rotación, sabiendo que el vértice $B$ se mueve con velocidad instantánea constante.