Comparación de posibles movimientos

De las siguientes cuatro figuras, solo una representa velocidades posibles de los extremos A y B de una barra rígida que realiza un movimiento plano. ¿Cuál?

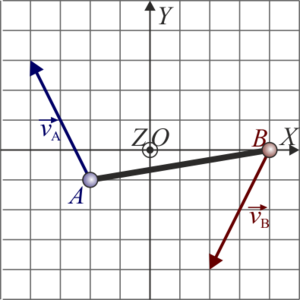
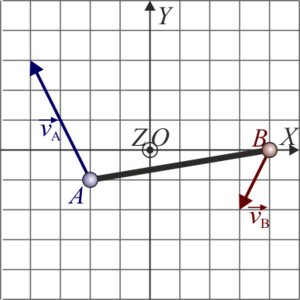
A	B
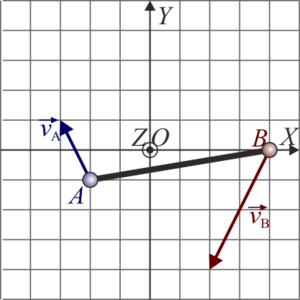
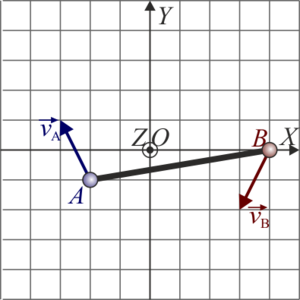
C	D

Para la barra anterior, ¿dónde se encuentra su centro instantáneo de rotación, según la cuadrícula de la figura?

¿Cuánto vale, en rad/s, la velocidad angular instantánea de este movimiento, si la cuadrícula representa m en distancias y m/s en velocidades?

Caso correcto

La respuesta correcta es la segunda.

Gráficamente, la posición del CIR se halla trazando las perpendiculares a las velocidades de A y B que pasan por A y B respectivamente. La intersección de estas dos perpendiculares es la posición buscada.

En este caso, cualquiera de las cuatro figuras conduce al mismo punto

${\overrightarrow {OI}}=2{\vec {\imath }}+{\vec {\jmath }}$

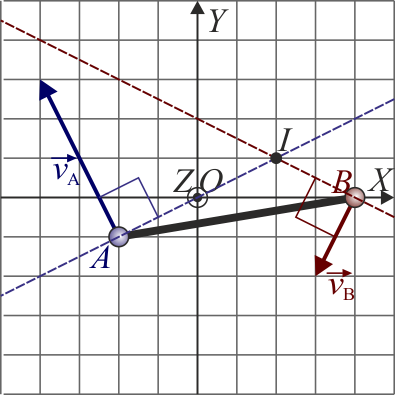
Una vez localizado el centro instantáneo de rotación, podemos usarlo para resolver la cuestión anterior. Puesto que la rapidez de un punto de un sólido es proporcional a la distancia al eje

$|{\vec {v}}_{P}|=|{\vec {\omega }}|\left|{\overrightarrow {IP}}\right|$

y el punto B está más cerca del CIR que el punto A, la solución correcta para las velocidades posibles es aquella que tiene menor rapidez para B que para A, la cual corresponde a la segunda opción de las respuestas.

Velocidad angular

De acuerdo con la ecuación para la rapidez de los puntos de un sólido tenemos que

$|{\vec {v}}_{B}|=|{\vec {\omega }}|\left|{\overrightarrow {IB}}\right|\qquad \Rightarrow \qquad |{\vec {\omega }}|={\frac {|{\vec {v}}_{B}|}{\left|{\overrightarrow {IB}}\right|}}$

En este caso,

$\left|{\overrightarrow {IB}}\right|={\sqrt {2^{2}+1^{2}}}\,\mathrm {m} ={\sqrt {5}}\,\mathrm {m} \qquad \qquad |{\vec {v}}_{B}|={\sqrt {1^{2}+2^{2}}}\,{\frac {\mathrm {m} }{\mathrm {s} }}={\sqrt {5}}\,{\frac {\mathrm {m} }{\mathrm {s} }}$

y por tanto

$|{\vec {\omega }}|=1\,{\frac {\mathrm {rad} }{\mathrm {s} }}$

El sentido lo da la regla de la mano derecha. La barra está girando en sentido horario y por tanto el vector velocidad angular va hacia adentro del plano, lo que corresponde al eje Z negativo. Por tanto

${\vec {\omega }}=-{\vec {k}}\,{\frac {\mathrm {rad} }{\mathrm {s} }}$

También puede llegarse a este reusltado sin haber determinado previamente el CIR. Tenemos que

${\vec {v}}_{A}={\vec {B}}+{\vec {\omega }}\times {\overrightarrow {BA}}$

y por tanto

$-2{\vec {\imath }}+4{\vec {\jmath }}=-{\vec {\imath }}-2{\vec {\jmath }}+(\omega {\vec {k}})\times (-6{\vec {\imath }}-{\vec {\jmath }})$

Calculamos el producto vectorial y separamos en componentes

$-2=-1+\omega \qquad \qquad 4=-2-6\omega \qquad \Rightarrow \qquad \omega =-1\,{\frac {\mathrm {rad} }{\mathrm {s} }}$

y en forma vectorial

${\vec {\omega }}=-{\vec {k}}\,{\frac {\mathrm {rad} }{\mathrm {s} }}$