Enunciado
Encuentra las reducciones cinemáticas instantáneas pedidas de cada uno de estos movimientos
- Una rueda de radio que gira con velocidad angular constante alrededor de un eje perpendicular a ella que pasa por su centro. Encuentra la reducción canónica.
- Una rueda de radio rueda sin deslizar sobre una superficie horizontal de modo que su centro avanza con velocidad uniforme . Encuentra la reducción en el centro y la reducción canónica.
- Una rueda de radio rueda y desliza con velocidad angular alrededor de un eje perpendicular a ella, de modo que el punto de contacto con el suelo tiene una vez relativa a éste de módulo . Encuentra la reducción en el punto de contacto y la reducción canónica.
- Un tornillo gira con velocidad angular uniforme y avanza con velocidad uniforme paralelamente a su eje. Encuentra la reducción en el punto más alto de la superficie frontal del tornillo y la reducción canónica.
Solución
Rueda girando alrededor de su centro
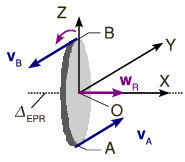
En este movimiento el eje de giro es siempre el mismo, la recta perpendicular a la rueda que pasa por su centro. Estamos pues ante una rotación permanente. La velocidad del centro de la rueda es nula en todo instante, pues el eje de giro pasa por ella. La figura adjunta ilustra la forma del campo de velocidades de los puntos de la rueda.
Un sistema de vectores cuyo campo de momentos es igual al campo de velocidades en los puntos de la rueda es un vector suelto , cuyo módulo es la velocidad angular , su dirección es perpendicular a la rueda y su sentido el dado por la regla de la mano derecha. La recta soporte del vector es el eje de giro. Así pues, la reducción en el centro de la rueda es la reducción canónica. Tenemos
Una vez tenemos esta reducción, podemos calcular la velocidad en cualquier punto del sólido a través de la ecuación del campo de velocidades. Así, en el punto tenemos
Este caso corresponde a una rotación pura, como se puede ver del hecho de que la velocidad de deslizamiento (el momento mínimo del s.v.d.) es nula.
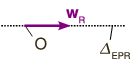
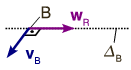
Resulta interesante comparar las reducciones canónicas y en otro punto. En la figura de la derecha vemos la reducción canónica arriba y la reducción en el punto . En la reducción canónica sólo aparece un vector suelto, , pues en los puntos del eje la velocidad es nula. En la reducción en el punto aparece el vector y un vector perpendicular a . En este caso el sistema equivalente de vectores deslizantes está compuesto por tres vectores, el vector y un par de vectores cuyo momento sea . Además, en este caso la recta soporte de no es el eje permanente de rotación. A partir de la reducción en , la velocidad en cualquier otro punto del sólido sería
Rueda que rueda sin deslizar
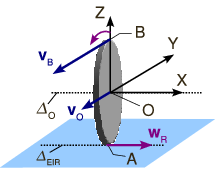
Consideramos a hora el caso en que tenemos un disco de radio que rueda sin deslizar sobre una superficie, de modo que el centro del disco avanza con una velocidad . El hecho de que ruede sin deslizar quiere decir que en cada instante la velocidad del punto de contacto con la superficie respecto a ésta es nula. La figura de la derecha muestra las velocidades en el punto de contacto (nula), el centro de la rueda () y el punto más alto, . Como la velocidad del punto es nula, el eje instantáneo de rotación tiene que pasar por el punto . Esto se debe a que en los puntos del eje la velocidad debe alcanzar su valor mínimo, y el cero es el valor más pequeño que puede tener. Por tanto, en cada instante el movimiento puede describirse como una rotación instantánea con vector rotación alrededor de una recta perpendicular al disco que pasa por el punto de contacto con el suelo.
La diferencia de este caso con el anterior es que la rotación no es permanente, es decir, el eje instantáneo de rotación va cambiando con el tiempo. En cada instante, será la recta perpendicular a la rueda que pasa por el punto de contacto entre la rueda y el suelo.
Como el eje instantáneo de rotación pasa por el punto , la reducción en ese punto es la reducción canónica. Tenemos
A partir de esta reducción, la velocidad en cualquier punto de la rueda es
Esto nos permite relacionar el vector rotación con el dato del enunciado, el módulo de la velocidad del centro de la rueda, . Escogiendo el sistema de ejes de la figura tenemos
Usando la reducción canónica, la velocidad en el centro de la rueda es
Por tanto, el vector rotación que describe este movimiento es
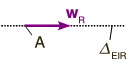
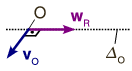
Como en el caso anterior, podemos comparar la reducción canónica con la reducción en otro punto, por ejemplo en el centro de la rueda, como dice el enunciado. La reducción canónica consiste en un único vector con recta soporte el eje instantáneo de rotación, como se muestra en la parte superior de la figura de la derecha. La reducción en el punto consiste en el vector deslizando sobre la recta y un par de vectores cuyo momento sea , como se muestra en la parte inferior de la figura. Es decir
Debe cumplirse que . A partir de la reducción en , la velocidad en cualquier punto del sólido es
Disco que rueda y desliza
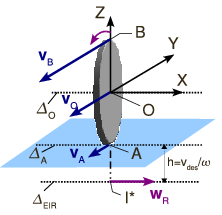
Vamos a estudiar ahora una situación en la que un disco de radio rueda y desliza sobre una superficie de modo que gira alrededor de un eje perpendicular a él con velocidad angular , y la velocidad del punto de contacto del disco respecto al suelo tiene módulo . La figura muestra la distribución de velocidades en el punto de contacto, el centro del disco y su punto superior. El enunciado no dice que el eje de rotación es perpendicular al disco. Entonces el vector es perpendicular a la velocidad de todos los puntos del sólido. Esto quiere decir que la velocidad mínima es cero, pues tenemos para cualquier del sólido. Por tanto, el movimiento instantáneo es una rotación pura.
Podemos obtener ya la reducción en el punto , el punto de contacto entre el sólido y el suelo. Conocemos la velocidad , que es la velocidad de deslizamiento, y el vector rotación . Escogiendo el sistema de ejes de la figura tenemos
Por tanto, la reducción en el punto es
¿Dónde está el eje instantáneo de rotación? Como tenemos la velocidad en un punto (el momento resultante del s.v.d.) y el vector rotación (la resultante del s.v.d.) podemos aplicar las técnicas de los s.v.d. para calcular la posición de un punto del eje instantáneo de rotación (el eje central del s.v.d.). Partiendo del puto
Vemos en la figura que el EIR es una recta situada a una distancia por debajo del suelo. Puede resultar chocante que el EIR no pase por un punto del sólido, para nada obliga a ello. Lo que tiene que ocurrir es que el campo de momentos del vector deslizando sobre el EIR reproduzca la velocidad de cada punto del sólido.
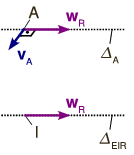
La reducción canónica es
De nuevo, es la reducción canónica correspondiente a una rotación pura. La reducción en el punto de contacto es
La figura muestra las dos reducciones, arriba la canónica y abajo la reducción en .
Tornillo que avanza

Veamos el caso de un tornillo que gira con velocidad angular uniforme y avanza con velocidad uniforme paralelamente a su eje. Al avanzar y girar, los puntos del eje central del tornillo tienen una velocidad que es paralela al propio eje. En los puntos fuera del eje, la velocidad tiene una componente paralela al eje y otra componente perpendicular debido a la rotación. La figura muestra las velocidades en el punto del eje de la cara de avance () y en los puntos superior () e inferior(). Así pues, la velocidad de los puntos del eje es mínima y su módulo es igual a la velocidad de avance del tornillo como un todo. Por tanto, el eje instantáneo de rotación y mínimo deslizamiento (EIRMD) es la línea que pasa por el punto . El vector rotación tiene como módulo la velocidad angular del enunciado y desliza sobre el EIRMD. La velocidad en el punto tiene como módulo la velocidad de avance del enunciado, , y como dirección y sentido la indicada en la figura. La reducción en el punto es la reducción canónica
El movimiento es helicoidal tangente, pues la velocidad mínima (el momento mínimo) es distinto de cero y el vector rotación (la resultante) también. La reducción canónica consta de un vector suelto, , deslizando sobre el EIRMD, y un par de vectores cuyo momento es .
La reducción en un punto fuera del eje central consta del vector deslizando sobre una recta paralela al EIRMD que pasa por ese punto, y un par de vectores cuyo momento sea la velocidad en ese punto. Si consideramos el punto tenemos
La reducción en es
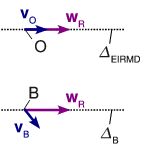
En este caso, el vector no es perpendicular al vector rotación, como en una rotación pura, sino que tiene una componente paralela a él. Esto se debe a que la velocidad mínima es distinta de cero y por tanto
donde es un vector unitario en la dirección y sentido de . La figura muestra arriba la reducción canónica y abajo la reducción en el punto .




































