Diferencia entre revisiones de «Problemas de cinemática del movimiento relativo (CMR)»
Secciones
| (No se muestran 12 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
= Problemas del boletín = | |||
==[[Giro de un triedro (G.I.A.) | Giro de un triedro ]]== | |||
[[Imagen:derivadas.gif|right]] | |||
Los triedros <math>O_1X_1Y_1Z_1</math> y <math>OX_0Y_0Z_0</math> están definidos de modo que sus orígenes y los ejes <math>O_1Z_1</math> coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme <math>\vec{\omega}_{01} = \omega\,\vec{k}_1 =\omega\,\vec{k}_0</math>, de modo que el ángulo <math>\theta</math> indicado en la figura es <math>\theta = \omega\, t</math>. | |||
#Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1". | |||
#Dado el vector <math>\vec{A}(t) = a\,\vec{\imath}_0</math> calcula | |||
<center> | |||
<math> | |||
\left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_1 \qquad\qquad \left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_0 | |||
</math> | |||
</center> | |||
#Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1"). | |||
#Haz el mismo cálculo para el vector <math>\vec{B}(t) = b\,t\,\vec{\imath}_0</math> | |||
==[[ Hélice de un avión que gira (G.I.A.) | Hélice de un avión que gira ]]== | |||
[[Imagen:avion_girando.gif|right]] | |||
El avión (sólido "0") de la figura se mueve de modo que el centro <math>C</math> de su hélice describe una circunferencia de radio <math>L</math>. La velocidad angular de este giro es uniforme y su módulo es <math>|\vec{\omega}_{01}|=\Omega</math>. Además, la hélice (sólido "2"), cuyo radio es <math>R</math>, gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad también uniforme y de módulo <math>|\vec{\omega}_{20}|=\omega</math>. Se pide | |||
#La reducción cinemática de los movimientos {01} y {20}. | |||
#Aplicando la composición de velocidades, la velocidad <math>\vec{v}_{21}^P</math> y aceleración <math>\vec{a}_{21}^P</math> del punto más alto de la hélice (punto <math>P</math> en la figura). | |||
# La reducción cinemática del movimiento {21} en <math>P</math> y la ecuación del E.I.R.M.D. ¿Qué tipo de movimiento describe la hélice respecto al sólido "1"? | |||
# Calcule numéricamente <math>|\vec{v}_{21}^P|</math> y <math>|\vec{a}_{21}^P|</math> para los valores <math>R=1\,\mathrm{m}</math>, <math>L=100\,\mathrm{m}</math>, <math>\omega=100\,\mathrm{rad/s}</math> y <math>\Omega=1\,\mathrm{rad/s}</math>. | |||
'''Nota:''' Se recomienda utilizar el triedro asociado al sólido "0" para resolver el problema. | |||
==[[Barras articuladas con barra fija (Nov. 2019) | Barras articuladas con barra fija ]]== | |||
[[File:MRGIC-2019-barras.png|right]] | |||
Una barra delgada de longitud <math>2\sqrt{2}b</math> (sólido "0") está articulada en el punto | |||
fijo <math>O</math>. En el otro extremo de la barra (punto <math>A</math>) se articula otra barra | |||
(sólido "2") de longitud <math>\sqrt{2}b</math>. A su vez, el otro extremo de la barra 2 (punto | |||
<math>B</math>) se articula en un pasador obligado a moverse sobre una barra fija | |||
vertical. En todo instante la velocidad del punto <math>B</math> es <math>\vec{v}_0= | |||
v_0\,\vec{\jmath}_1</math>, con <math>v_0>0</math> y constante. En el instante indicado en la | |||
figura las dos barra son perpendiculares y forman un ángulo <math>\pi/4</math> con la | |||
barra fija vertical. Todas las preguntas siguientes corresponden a este instante. | |||
# Determina el vector de posición del punto <math>B</math> es | |||
# Encuentra gráficamente y analíticamente la posición de los C.I.R. de los movimientos {01}, {20} y {21}. | |||
#Calcula los vectores rotación de los movimientos {21} y {01}. | |||
#Calcula el vector aceleración del movimiento {21}. | |||
= Otros problemas = | |||
==Rotaciones finitas sucesivas de 90°== | ==Rotaciones finitas sucesivas de 90°== | ||
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden. | Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden. | ||
| Línea 9: | Línea 51: | ||
==Rotaciones finitas sucesivas== | ==Rotaciones finitas sucesivas== | ||
¿Cómo quedan los resultados del [[Rotaciones_finitas_sucesivas_de_90°_(CMR)|problema anterior]] si los giros no son de +90° sino de <math>\beta=\ | ¿Cómo quedan los resultados del [[Rotaciones_finitas_sucesivas_de_90°_(CMR)|problema anterior]] si los giros no son de +90° sino de <math>\beta=\arctan(3/4)</math>? (recomendable hacer los cálculos con ayuda de un ordenador). | ||
[[Rotaciones finitas sucesivas (CMR)|Solución]] | [[Rotaciones finitas sucesivas (CMR)|Solución]] | ||
| Línea 31: | Línea 73: | ||
<table class="bordeado"> | <table class="bordeado"> | ||
<tr> | <tr> | ||
<td>[[Archivo:vagonetas-relativa.01.png]]</td> | <td>[[Archivo:vagonetas-relativa.01.png|300px]]</td> | ||
<td>[[Archivo:vagonetas-relativa.02.png]]</td> | <td>[[Archivo:vagonetas-relativa.02.png|300px]]</td> | ||
<td rowspan="3">[[Archivo:vagonetas-relativa.05.png]]</td> | <td rowspan="3">[[Archivo:vagonetas-relativa.05.png|300px]]</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Línea 40: | Línea 82: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>[[Archivo:vagonetas-relativa.03.png]]</td> | <td>[[Archivo:vagonetas-relativa.03.png|300px]]</td> | ||
<td>[[Archivo:vagonetas-relativa.04.png]]</td> | <td>[[Archivo:vagonetas-relativa.04.png|300px]]</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Línea 49: | Línea 91: | ||
</tr> | </tr> | ||
</table> | </table> | ||
[[Velocidad relativa de dos vagones|''' | [[Velocidad relativa de dos vagones|Solución]] | ||
==Peonza rodante oblicua== | |||
Una peonza está formada por una varilla de longitud <math>\ell=20\,\mathrm{cm}</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje <math>OZ_1</math> con rapidez <math>v_0=48\,\mathrm{cm/s}</math>. El disco rueda sin deslizar sobre el plano <math>OX_1Y_1</math>, de manera que en todo instante la velocidad del punto de contacto A es nula. | |||
Para este movimiento, determine: | |||
# La velocidad angular del sólido en el movimiento {21}. | |||
# La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en <math>25\vec{k}\,\mathrm{cm}</math>, considerado como punto del sólido. | |||
# La aceleración angular del sólido. | |||
# La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido. | |||
<center>[[Archivo:Peonza-rodante.png|400px]] [[Archivo:Peonza-rodante-b.png]]</center> | |||
Sugerencia: Introduzca un sólido intermedio “0” que simplemente gira en torno al eje OZ_1, de manera que el eje OX_0 siempre pasa por el O y por el punto de contacto con el suelo. | |||
[[Peonza rodante oblicua (CMR)|Solución]] | |||
==Peonza rodante horizontal== | |||
Un disco de radio ''R'' (“sólido 3”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud ''h'' (“sólido 2”). Este eje está montado sobre un soporte vertical fijo de altura ''R''. El disco rueda sin deslizar sobre la superficie horizontal <math>z=0</math> (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje <math>{OX}_2</math> es a lo largo de la barra horizontal y <math>{OZ}_2={OZ}_1</math> en todo momento. Sea <math>\phi(t)</math> el ángulo que el eje <math>{OX}_2</math> forma con el <math>{OX}_1</math>. En un instante dado <math>\phi=0\,</math>,<math>\dot{\phi}=\Omega</math>,<math>\ddot{\phi}=\alpha</math>. Para ese instante: | |||
# Determine los vectores <math>\vec{\omega}_{21}</math>, <math>\vec{\omega}_{31}</math> y <math>\vec{\omega}_{32}</math>. | |||
# Halle la posición de los ejes instantáneos de rotación en los movimientos {21}, {32} y {31}. | |||
# Calcule las velocidades en el movimiento {31} y el {21} del punto A de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco. | |||
# Halle las aceleraciones angulares <math>\vec{\alpha}_{21}</math>, <math>\vec{\alpha}_{32}</math> y <math>\vec{\alpha}_{31}</math>. | |||
# Calcule las aceleraciones en los movimientos {31} y {32} de los puntos A, G y D del apartado (3). | |||
<center>[[Archivo:Peonza-rodante-horizontal.png|400px]]</center> | |||
[[Peonza rodante horizontal (CMR)|Solución]] | |||
==Bola que rueda en carril== | |||
Una bola (sólido “2”), de radio <math>R=15\,\mathrm{cm}</math>, se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios <math>b=7\,\mathrm{cm}</math> y <math>c=25\,\mathrm{cm}</math>, situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que en todo instante, rueda sin deslizar sobre ambos carriles. | |||
Consideramos como sólido móvil intermedio (“sólido 0”) al plano <math>O_1 X_0 Z_0</math> que contiene en todo instante al centro C de la esfera (ver figura). | |||
<center>[[Archivo:Bola-carril.png|400px]]</center> | |||
# ¿Cuántos grados de libertad tiene este sistema? | |||
# Sea θ(t) el ángulo que forma el eje <math>{OX}_0</math> con el <math>{OX}_1</math>. Con ayuda del sólido intermedio halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}. | |||
# Halle las velocidades angulares y aceleraciones angulares de los movimientos {21}, {20} y {01} | |||
# Para el punto de la bola en contacto con el carril de mayor radio (punto B), determine <math>\vec{v}_20^B</math> y <math>\vec{a}_{21}^B</math>. | |||
[[Bola que rueda en carril (CMR)|Solución]] | |||
==Barra que desliza en eje rotatorio== | |||
El armazón de barras paralelas a los ejes <math>OX_0</math> y <math>OZ_0</math> (sólido “0”) rota alrededor del eje vertical fijo OZ1, de tal modo que el eje OX0 permanece siempre contenido en el plano horizontal fijo OX1Y1 (sólido “1”). Por otra parte, la varilla AB (sólido “2”), de longitud b, se mueve de forma que su extremo A desliza a lo largo del eje OX0, mientras que su extremo B desliza a lo largo del eje OZ0. Utilizando los ángulos θ y φ (definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine: | |||
# La velocidad de A, B y G (siendo G el punto medio de la barra) en los movimientos {01}, {20} y {21}, así como la velocidad angular <math>\vec{\omega}_{21}</math>. | |||
# ¿De qué tipo es el movimiento {21}? ¿Dónde está su EIRMD? | |||
# La aceleración angular <math>\vec{\alpha}_{21}</math> y las aceleraciones de A, B y G en los movimientos {01}, {20} y {21} | |||
<center>[[Archivo:Barra-desliza-rota.png|400px]]</center> | |||
[[Barra que desliza en eje rotatorio (CMR)|Solución]] | |||
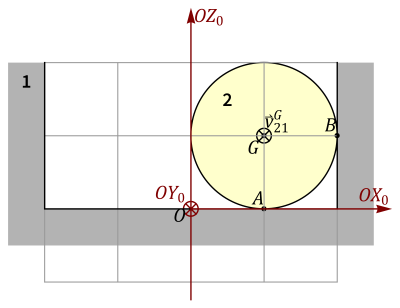
==Esfera en recipiente cilíndrico== | |||
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante <math>v_0</math> alrededor del eje vertical. | |||
Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje <math>{OZ}_1</math>=OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano <math>{OX}_0Z_0</math> . Con ayuda de este sistema determine y exprese: | |||
# Las velocidades angulares <math>\vec{\omega}_{01}</math>, <math>\vec{\omega}_{21}</math> y <math>\vec{\omega}_{20}</math> | |||
# La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura) | |||
# Las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math> | |||
# Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1. | |||
<center>[[Archivo:Esfera-recipiente-cilindrico.png|400px]]</center> | |||
[[Esfera en recipiente cilíndrico|Solución]] | |||
Revisión actual - 16:33 17 oct 2024
Problemas del boletín
Giro de un triedro
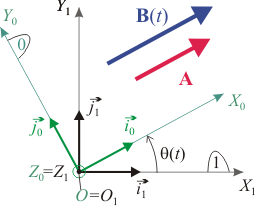
Los triedros y están definidos de modo que sus orígenes y los ejes coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme , de modo que el ángulo indicado en la figura es .
- Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1".
- Dado el vector calcula
- Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1").
- Haz el mismo cálculo para el vector
Hélice de un avión que gira
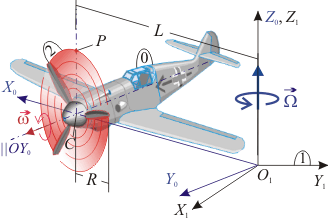
El avión (sólido "0") de la figura se mueve de modo que el centro de su hélice describe una circunferencia de radio . La velocidad angular de este giro es uniforme y su módulo es . Además, la hélice (sólido "2"), cuyo radio es , gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad también uniforme y de módulo . Se pide
- La reducción cinemática de los movimientos {01} y {20}.
- Aplicando la composición de velocidades, la velocidad y aceleración del punto más alto de la hélice (punto en la figura).
- La reducción cinemática del movimiento {21} en y la ecuación del E.I.R.M.D. ¿Qué tipo de movimiento describe la hélice respecto al sólido "1"?
- Calcule numéricamente y para los valores , , y .
Nota: Se recomienda utilizar el triedro asociado al sólido "0" para resolver el problema.
Barras articuladas con barra fija
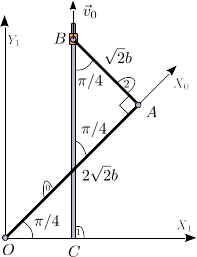
Una barra delgada de longitud (sólido "0") está articulada en el punto fijo . En el otro extremo de la barra (punto ) se articula otra barra (sólido "2") de longitud . A su vez, el otro extremo de la barra 2 (punto ) se articula en un pasador obligado a moverse sobre una barra fija vertical. En todo instante la velocidad del punto es , con y constante. En el instante indicado en la figura las dos barra son perpendiculares y forman un ángulo con la barra fija vertical. Todas las preguntas siguientes corresponden a este instante.
- Determina el vector de posición del punto es
- Encuentra gráficamente y analíticamente la posición de los C.I.R. de los movimientos {01}, {20} y {21}.
- Calcula los vectores rotación de los movimientos {21} y {01}.
- Calcula el vector aceleración del movimiento {21}.
Otros problemas
Rotaciones finitas sucesivas de 90°
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a . ¿Cuál es la matriz de rotación que permite pasar de las coordenadas (X,Y,Z) en la posición final del sistema ligado a las coordenadas en el sistema fijo (x,y,z)? ¿Cuál es el eje de rotación de la composición? ¿Cuál es el ángulo girado?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a ?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a ?
- Si se realizan las dos rotaciones del apartado (a) (1º +90° en torno a ; 2º +90° en torno a ) y a continuación se gira −90° en torno a seguido de −90° en torno a , ¿vuelve el sólido a su posición inicial? Si no es así, ¿cuál es el eje de rotación y el ángulo girado?
Rotaciones finitas sucesivas
¿Cómo quedan los resultados del problema anterior si los giros no son de +90° sino de ? (recomendable hacer los cálculos con ayuda de un ordenador).
Composición de dos rotaciones de 90°
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación −90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación −90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
Velocidad relativa de dos vagones
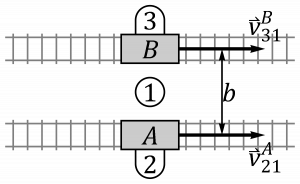
Se tienen dos vagonetas A y B (sólidos “2” y “3”), que avanzan por raíles sobre el suelo horizontal (sólido “1”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades . El vector de posición relativo entre las dos vagonetas es . Los ejes de los tres sistemas se toman paralelos de forma que los vectores de las respectivas bases son coincidentes en ese instante. Halle las velocidades relativas y en los siguientes casos:
- Las vagonetas se mueven por vías rectilíneas paralelas.
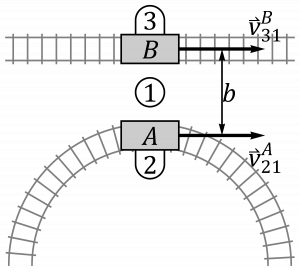
- La vagoneta B se mueve por una vía circular de radio R, mientras que A se mueve por una vía rectilínea. El instante descrito es el de máximo acercamiento entre las dos vías.
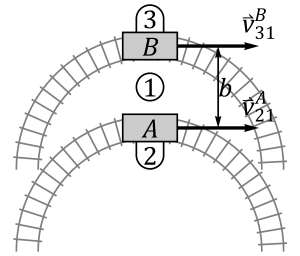
- Las dos se mueven por vías circulares concéntricas, de radios R y R+b, respectivamente.
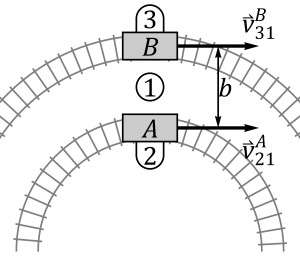
- Las dos se mueven por arcos de circunferencia de radio R con centros hacia el mismo lado.
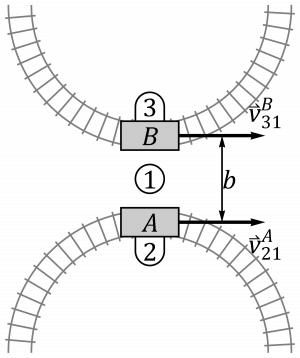
- Las dos se mueven por arcos de circunferencia de radio R con centros en lados opuestos.
 |
 |
 |
| (1) | (2) | |
|---|---|---|
 |
 |
|
| (3) | (4) | (5) |
Peonza rodante oblicua
Una peonza está formada por una varilla de longitud ensartada en un disco de radio . Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje con rapidez . El disco rueda sin deslizar sobre el plano , de manera que en todo instante la velocidad del punto de contacto A es nula. Para este movimiento, determine:
- La velocidad angular del sólido en el movimiento {21}.
- La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en , considerado como punto del sólido.
- La aceleración angular del sólido.
- La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.
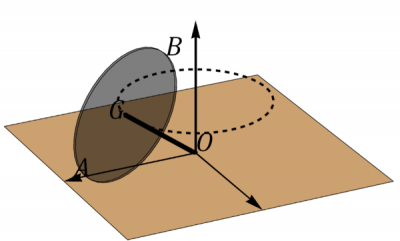
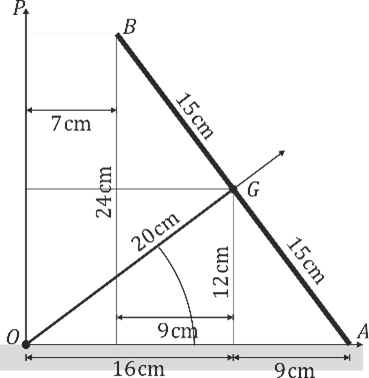
Sugerencia: Introduzca un sólido intermedio “0” que simplemente gira en torno al eje OZ_1, de manera que el eje OX_0 siempre pasa por el O y por el punto de contacto con el suelo.
Peonza rodante horizontal
Un disco de radio R (“sólido 3”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 2”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje es a lo largo de la barra horizontal y en todo momento. Sea el ángulo que el eje forma con el . En un instante dado ,,. Para ese instante:
- Determine los vectores , y .
- Halle la posición de los ejes instantáneos de rotación en los movimientos {21}, {32} y {31}.
- Calcule las velocidades en el movimiento {31} y el {21} del punto A de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco.
- Halle las aceleraciones angulares , y .
- Calcule las aceleraciones en los movimientos {31} y {32} de los puntos A, G y D del apartado (3).
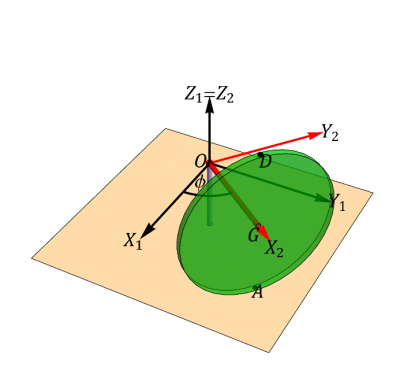
Bola que rueda en carril
Una bola (sólido “2”), de radio , se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios y , situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que en todo instante, rueda sin deslizar sobre ambos carriles. Consideramos como sólido móvil intermedio (“sólido 0”) al plano que contiene en todo instante al centro C de la esfera (ver figura).
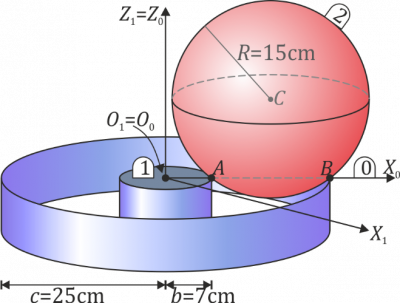
- ¿Cuántos grados de libertad tiene este sistema?
- Sea θ(t) el ángulo que forma el eje con el . Con ayuda del sólido intermedio halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
- Halle las velocidades angulares y aceleraciones angulares de los movimientos {21}, {20} y {01}
- Para el punto de la bola en contacto con el carril de mayor radio (punto B), determine y .
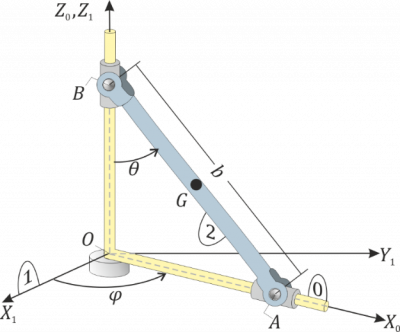
Barra que desliza en eje rotatorio
El armazón de barras paralelas a los ejes y (sólido “0”) rota alrededor del eje vertical fijo OZ1, de tal modo que el eje OX0 permanece siempre contenido en el plano horizontal fijo OX1Y1 (sólido “1”). Por otra parte, la varilla AB (sólido “2”), de longitud b, se mueve de forma que su extremo A desliza a lo largo del eje OX0, mientras que su extremo B desliza a lo largo del eje OZ0. Utilizando los ángulos θ y φ (definidos en la figura), así como sus derivadas temporales de primer y segundo orden, determine:
- La velocidad de A, B y G (siendo G el punto medio de la barra) en los movimientos {01}, {20} y {21}, así como la velocidad angular .
- ¿De qué tipo es el movimiento {21}? ¿Dónde está su EIRMD?
- La aceleración angular y las aceleraciones de A, B y G en los movimientos {01}, {20} y {21}
Esfera en recipiente cilíndrico
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante alrededor del eje vertical. Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje =OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano . Con ayuda de este sistema determine y exprese:
- Las velocidades angulares , y
- La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura)
- Las aceleraciones angulares , y
- Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1.