Primera Prueba de Control 2014/15 (G.I.C.)

Partícula moviéndose sobre una parábola

Una partícula se mueve siguiendo la trayectoria descrita por la curva de ecuaciones implícitas $y=A(1-x^{2}/A^{2})$ y $z=0$, donde $A$ es una constante. La coordenada $x$ varía en el intervalo $x\in [0,A]$.

1. Determina el vector tangente en función de la posición de la partícula
2. Suponiendo que en $t=0$ la distancia recorrida es $s=0$ encuentra la expresión que da la distancia total recorrida sobre la curva.
3. ¿Cuál es el vector normal a la trayectoria en $x=0$?

Partícula con curvatura y aceleración tangencial dependientes del tiempo

Una partícula se mueve de modo que, en todo instante, su curvatura es $\kappa =At$ y su aceleración tangencial es $a_{T}=Bt$, siendo $A$ y $B$ constantes. Suponemos que en el instante inicial la partícula está en reposo.

1. ¿Cuáles son las unidades base de las constantes en el SI?
2. Suponiendo que en $t=0$ se tiene $s=0$, calcula la distancia recorrida en cada instante de tiempo
3. Calcula el módulo de la aceleración en cada instante.

Partícula con dos muelles apoyada sobre un plano vertical

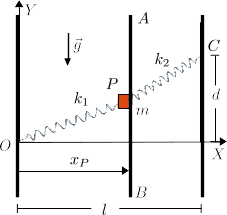
Un partícula de masa $m$ reposa sin rozamiento sobre un plano vertical definido por los puntos $A$ y $B$ de la figura. Está atada a dos muelles de constantes elásticas $k_{1}$ y $k_{2}$ y longitud natural nula, anclados en los puntos $O$ y $C$, respectivamente. La partícula no puede deplazarse a lo largo del eje $OZ$. El plano $AB$ puede desplazarse a lo largo del eje $OX$ de modo que se mantiene siempre vertical.

1. Dibuja el diagrama de cuerpo libre de la partícula.
2. ¿Que condición debe cumplirse para que el punto de equilibrio de la masa esté sobre el eje $OX$
3. ¿Qué condición debe cumplir $x_{P}$ para que el plano $AB$ ejerza una fuerza sobre la partícula?
4. Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático $\mu _{e}$. Si $y_{m}$ es la coordenada de la partícula sobre el eje $OY$, calcula el módulo de la fuerza de rozamiento.
5. En la situación con rozamiento, supongamos que $k_{1}=k_{2}=k$, $mg=2kd$, $d=l$ y $x_{P}=l/4$. ¿Cuál es el rango de posiciones de equilibrio de la partícula sobre el plano?

Masas deslizando sobre un plano horizontal

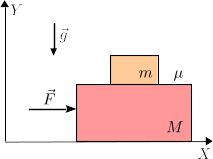
Las dos masas de la derecha se mueven horizontalmente. El contacto de la masa $M$ sobre el suelo es liso, mientras que el contacto entre las dos masas es rugoso con un coeficiente de rozamiento estático $\mu$. Una fuerza ${\vec {F}}$ horizontal actúa sobre la masa $M$.

1. Si durante el movimiento las dos masas mantienen su posición relativa, ¿cuál es su aceleración?
2. Calcula la fuerza total que la masa $m$ ejerce sobre la masa $M$.
3. ¿Qué condición debe cumplir $|{\vec {F}}|$ para que la masa $m$ no deslice respecto de la masa $M$?