Diferencia entre las páginas «Archivo:MR 2018 barras muelle enunciado.png» y «Sep. 2018 (M.R.) Barra rotando alrededor de barra horizontal con muelle»
Sin resumen de edición |
(Página creada con «= Enunciado = right Una barra de longitud <math>2d</math> y masa despreciable (sólido "0") puede rotar alrededor del eje <math>OZ_1</math>. El punto <math>O</math> de la barra es fijo. La barra "0" siempre está contenida en el plano <math>OX_1Y_1</math>. Otra barra, también de longitud <math>2d</math> y masa <math>m</math> (sólido "2"), está conectada a la barra "0" por un pasador en el punto <math>A</math>. El pa…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Imagen:MR_2018_barras_muelle_enunciado.png|right]] | |||
Una barra de longitud <math>2d</math> y masa despreciable (sólido "0") puede rotar alrededor del eje <math>OZ_1</math>. El punto <math>O</math> de la barra es fijo. La barra "0" siempre está contenida en el plano <math>OX_1Y_1</math>. Otra barra, también de longitud <math>2d</math> y masa <math>m</math> (sólido "2"), está conectada a la barra "0" por un pasador en el punto <math>A</math>. El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica <math>k</math> y longitud natural nula <math>l_0=d</math> conecta los puntos <math>O</math> y <math>A</math>. | |||
#Determina las reducciones cinemáticas <math>\{01\}, \{20\}</math> y <math>\{21\}</math> en <math>G</math>. | |||
#Calcula el momento cinético de la barra "2" respecto de <math>G</math>. | |||
#A partir de ahora suponemos que <math>\phi=\dot{\phi}=\ddot{\phi}=0</math>, es decir, la coordenada <math>\phi</math> ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema. | |||
#En <math>t=0</math> tenemos <math>s(0)=d</math>, <math>\theta(0)=-\pi/2</math>, <math>\dot{s}(0)=0</math> y <math>\dot{\theta}=0</math> (<math>\phi</math> sigue estando fijada). La barra "2" recibe una percusión <math>\vec{\hat{F}} = [\hat{F}_0, 0, \hat{F}_0]_1</math> en el punto B. Determina el estado del sistema justo después de la percusión. | |||
= Solución = | |||
== Reducciones cinemáticas en <math>G</math> == | |||
Para el movimiento {01} tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \dot{\phi}\,\vec{k}_0, \qquad \vec{v}^{\,O}_{01} = \vec{0}. | |||
</math> | |||
</center> | |||
Teniendo en cuenta que | |||
<center> | |||
<math> | |||
\overrightarrow{OG} = s\,\vec{\imath}_0 + d\cos{\theta}\,\vec{\jmath}_0 + d\,\mathrm{sen}\,\theta\,\vec{k}_0, | |||
</math> | |||
</center> | |||
tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG} | |||
=-d\dot{\phi}\cos\theta\,\vec{\imath}_0 + s\dot{\phi}\,\vec{\jmath}_0. | |||
</math> | |||
</center> | |||
Para el movimiento {20} | |||
<center> | |||
<math> | |||
\vec{\omega}_{20} = \dot{\theta}\,\vec{\imath}_0, \qquad \vec{v}^{\,A}_{01} = \dot{s}\,\vec{\imath}_0. | |||
</math> | |||
</center> | |||
Teniendo en cuenta que | |||
<center> | |||
<math> | |||
\overrightarrow{AG} = d\cos{\theta}\,\vec{\jmath}_0 + d\,\mathrm{sen}\,\theta\,\vec{k}_0, | |||
</math> | |||
</center> | |||
tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{20} = \dot{s}\,\vec{\imath}_0 -d\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\jmath}_0 + d\dot{\theta}\cos\theta\,\vec{k}_0. | |||
</math> | |||
</center> | |||
Para el movimiento {21} usamos las leyes de composición | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} =\dot{\theta}\,\vec{\imath}_0 + \dot{\phi}\,\vec{k}_0.\\ | |||
\\ | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01} = | |||
(\dot{s} - d\dot{\phi}\cos\theta)\,\vec{\imath}_0 -d\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\jmath}_0 + d\dot{\theta}\cos\theta\,\vec{k}_0. | |||
\end{array} | |||
</math> | |||
</center> | |||
== Momento cinético de la barra respecto a <math>G</math> == | |||
El momento cinético respecto al Centro de Masas <math>G</math> es | |||
<center> | |||
<math> | |||
\vec{L}_G = \overset\leftrightarrow{I}_G\cdot\vec{\omega}_{21}. | |||
</math> | |||
</center> | |||
El tensor de inercia es | |||
<center> | |||
<math> | |||
\overset\leftrightarrow{I}_G | |||
\left[ | |||
\begin{array}{ccc} | |||
I_0 & 0 & 0\\ | |||
0 & I_0 & 0\\ | |||
0 & 0 & 0 | |||
\end{array} | |||
\right]_2 | |||
\qquad\qquad | |||
I_0 = \dfrac{1}{12}m(2d)^2 = \dfrac{1}{3}md^2. | |||
</math> | |||
</center> | |||
Hay que expresar <math>\vec{\omega}_{21}</math> en la base "2". Del dibujo tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\imath}_0 = \vec{\imath}_2,\\ | |||
\vec{\jmath}_0 = \mathrm{sen}\,\theta\,\vec{\jmath}_2 + \cos\theta\,\vec{k}_2,\\ | |||
\vec{k}_0 = -\cos\theta\,\vec{\jmath}_2 + \mathrm{sen}\,\theta\,\vec{k}_2. | |||
\end{array} | |||
</math> | |||
</center> | |||
Entonces | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = \dot{\theta}\,\vec{\imath}_0 + \dot{\phi}\,\vec{k}_0 | |||
= | |||
\dot{\theta}\,\vec{\imath}_2 -\dot{\phi}\cos\theta\,\vec{\jmath}_0 + \dot{\phi}\,\mathrm{sen}\,\theta\,\vec{k}_2. | |||
</math> | |||
</center> | |||
El momento cinético es | |||
<center> | |||
<math> | |||
\vec{L}_G | |||
= | |||
\left[ | |||
\begin{array}{ccc} | |||
I_0 & 0 & 0\\ | |||
0 & I_0 & 0\\ | |||
0 & 0 & 0 | |||
\end{array} | |||
\right]_2 | |||
\left[ | |||
\begin{array}{c} | |||
\dot{\theta} \\ -\dot{\phi}\cos\theta \\ \dot{\phi}\,\mathrm{sen}\,\theta | |||
\end{array} | |||
\right]_2 | |||
= | |||
\left[ | |||
\begin{array}{c} | |||
I_0\dot{\theta} \\ -I_0\dot{\phi}\cos\theta \\ 0 | |||
\end{array} | |||
\right]_2 | |||
</math> | |||
</center> | |||
== Ecuaciones de Lagrange == | |||
Al restringir el grado de libertad <math>\phi</math>, el problema tiene sólo dos grados de libertad <math>\{s, \theta\}</math>. La reducción cinemática y el momento angular quedan | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\omega}_{21} = [\dot{\theta},\, 0,\, 0]_0\\ | |||
\\ | |||
\vec{v}^{\,G}_{21} = | |||
[\dot{s},\, -d\dot{\theta}\,\mathrm{sen}\,\theta\, d\dot{\theta}\cos\theta]_0\\ | |||
\\ | |||
\vec{L}_G = [I_0\dot{\theta}, \, 0, \, 0]_0. | |||
\end{array} | |||
</math> | |||
</center> | |||
=== Energía cinética === | |||
Tenemos | |||
<center> | |||
<math> | |||
T = T_{tra} + T_{rot} | |||
</math> | |||
</center> | |||
Para la energía cinética de traslación | |||
<center> | |||
<math> | |||
T_{tra} = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 | |||
= | |||
\dfrac{1}{2}m(\dot{s}^2 + d^2\dot{\theta}^2). | |||
</math> | |||
</center> | |||
La de rotación es | |||
<center> | |||
<math> | |||
T_{rot} = \dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} | |||
= | |||
\dfrac{1}{6}md^2\dot{\theta}^2. | |||
</math> | |||
</center> | |||
Hemos usado la expresión de <math>\vec{\omega}_{21}</math> para calcular el producto escalar con el momento cinético <math>\vec{L}_G</math>. Entonces | |||
<center> | |||
<math> | |||
T = \dfrac{1}{6}m(3\dot{s}^2 + 4d^2\dot{\theta}^2). | |||
</math> | |||
</center> | |||
=== Energía potencial === | |||
Contribuyen el muelle y la gravedad | |||
<center> | |||
<math> | |||
U_g = m g d\,\mathrm{sen}\,\theta, \qquad U_k = \dfrac{1}{2}k(s-d)^2. | |||
</math> | |||
</center> | |||
Para la energía potencial gravitatoria hemos tomado como referencia el plano <math>OX_1Y_1</math>. La energía potencial total es | |||
<center> | |||
<math> | |||
U = U_g + U_k = | |||
m g d\,\mathrm{sen}\,\theta + \dfrac{1}{2}k(s-d)^2. | |||
</math> | |||
</center> | |||
=== Ecuaciones de Lagrange === | |||
La función de Lagrange es | |||
<center> | |||
<math> | |||
L = T - U = | |||
\dfrac{1}{6}m(3\dot{s}^2 + 4d^2\dot{\theta}^2) - | |||
m g d\,\mathrm{sen}\,\theta - \dfrac{1}{2}k(s-d)^2. | |||
</math> | |||
</center> | |||
Ecuación de Lagrange para <math>s</math>: | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\dfrac{\partial L}{\partial \dot{s}} = m\dot{s},\\ | |||
\\ | |||
\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{s}}\right) = m\ddot{s},\\ | |||
\\ | |||
\dfrac{\partial L}{\partial s} = -k(s-d). | |||
\end{array} | |||
\right\} | |||
\to | |||
\ddot{s} + \dfrac{k}{m}(s-d) = 0 | |||
</math> | |||
</center> | |||
Ecuación de Lagrange para <math>\theta</math>: | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\dfrac{\partial L}{\partial \dot{\theta}} = \dfrac{4}{3}md^2\dot{\theta},\\ | |||
\\ | |||
\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial \dot{\theta}}\right) = \dfrac{4}{3}md^2\ddot{\theta},\\ | |||
\\ | |||
\dfrac{\partial L}{\partial \theta} = -mgd\cos\theta. | |||
\end{array} | |||
\right\} | |||
\to | |||
\ddot{\theta} + \dfrac{3g}{4d}\cos\theta=0. | |||
</math> | |||
</center> | |||
En este caso las dos ecuaciones están desacopladas. | |||
== Percusión == | |||
El estado inicial del sistema es | |||
<center> | |||
<math> | |||
s(0) = d, \qquad \dot{s}(0) = 0, \qquad \theta(0) = -\pi/2, \qquad \dot{\theta}(0)=0. | |||
</math> | |||
</center> | |||
La percusión se aplica en <math>B</math> y vale <math>\vec{\hat{F}} = [\hat{F}_0, 0, \hat{F}_0]</math>. Vamos a necesitar la velocidad absoluta del punto <math>B</math>. Teniendo en cuenta que <math>\overrightarrow{GB} = [0,d\cos\theta, d\,\mathrm{sen}\,\theta]_0 </math>, tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,B}_{21} = \vec{v}^{\,G}_{21} + \vec{\omega}_{21}\times\overrightarrow{GB} = | |||
[\dot{s}, -2d\dot{\theta}\,\mathrm{sen}\,\theta, 2d\dot{\theta}\cos\theta]_0. | |||
</math> | |||
</center> | |||
Los momentos generalizados son | |||
<center> | |||
<math> | |||
p_s = \dfrac{\partial L}{\partial \dot{s}} = m\dot{s}, \qquad | |||
p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}} = \dfrac{4}{3}md^2\dot{\theta}. | |||
</math> | |||
</center> | |||
Las ecuaciones de Lagrange impulsivas son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\Delta p_s = \hat{Q}^{NC}_s = \left.\vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{s}}\right|_{t=0},\\ | |||
\\ | |||
\Delta p_{\theta} = \hat{Q}^{NC}_s = \left.\vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{\theta}}\right|_{t=0}. | |||
\end{array} | |||
</math> | |||
</center> | |||
Como se parte del reposo | |||
<center> | |||
<math> | |||
\Delta p_s = m\dot{s}^+, \qquad \Delta p_{\theta} = \dfrac{4}{3}md^2\dot{\theta}^+. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{s}} = [1,\,0,\,0]_0, | |||
\qquad | |||
\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{\theta}} = [0,\, -2d\,\mathrm{sen}\,\theta, \, 2d\cos\theta ]_0. | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | |||
<math> | |||
\left.\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{s}}\right|_{t=0} = [1,\,0,\,0]_0, | |||
\qquad | |||
\left.\dfrac{\partial\vec{v}^{\,B}_{21}}{\partial \dot{\theta}}\right|_{t=0} = [0,\, 2d, \, 0 ]_0. | |||
</math> | |||
</center> | |||
Las percusiones generalizadas son | |||
<center> | |||
<math> | |||
Q^{NC}_{s} = \hat{F}_0, \qquad Q^{NC}_{\theta} = 0. | |||
</math> | |||
</center> | |||
Y el estado después de la percusión es | |||
<center> | |||
<math> | |||
\dot{s}(0^+) = \dfrac{\hat{F}_0}{m}, \qquad \dot{\theta}(0^+) = 0. | |||
</math> | |||
</center> | |||
[[Categoría:Problemas de mecánica analítica]] | |||
[[Categoría:Problemas de Dinámica Analítica]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión actual - 12:49 8 nov 2023
Enunciado
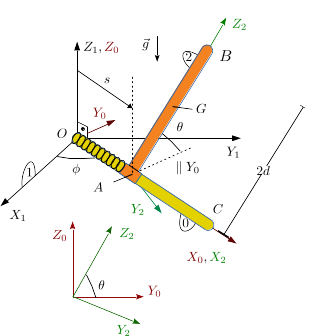
Una barra de longitud y masa despreciable (sólido "0") puede rotar alrededor del eje . El punto de la barra es fijo. La barra "0" siempre está contenida en el plano . Otra barra, también de longitud y masa (sólido "2"), está conectada a la barra "0" por un pasador en el punto . El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica y longitud natural nula conecta los puntos y .
- Determina las reducciones cinemáticas y en .
- Calcula el momento cinético de la barra "2" respecto de .
- A partir de ahora suponemos que , es decir, la coordenada ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema.
- En tenemos , , y ( sigue estando fijada). La barra "2" recibe una percusión en el punto B. Determina el estado del sistema justo después de la percusión.
Solución
Reducciones cinemáticas en
Para el movimiento {01} tenemos
Teniendo en cuenta que
tenemos
Para el movimiento {20}
Teniendo en cuenta que
tenemos
Para el movimiento {21} usamos las leyes de composición
Momento cinético de la barra respecto a
El momento cinético respecto al Centro de Masas es
El tensor de inercia es
Hay que expresar en la base "2". Del dibujo tenemos
Entonces
El momento cinético es
Ecuaciones de Lagrange
Al restringir el grado de libertad , el problema tiene sólo dos grados de libertad . La reducción cinemática y el momento angular quedan
Energía cinética
Tenemos
Para la energía cinética de traslación
La de rotación es
Hemos usado la expresión de para calcular el producto escalar con el momento cinético . Entonces
Energía potencial
Contribuyen el muelle y la gravedad
Para la energía potencial gravitatoria hemos tomado como referencia el plano . La energía potencial total es
Ecuaciones de Lagrange
La función de Lagrange es
Ecuación de Lagrange para :
Ecuación de Lagrange para :
En este caso las dos ecuaciones están desacopladas.
Percusión
El estado inicial del sistema es
La percusión se aplica en y vale . Vamos a necesitar la velocidad absoluta del punto . Teniendo en cuenta que , tenemos
Los momentos generalizados son
Las ecuaciones de Lagrange impulsivas son
Como se parte del reposo
Tenemos
Por tanto
Las percusiones generalizadas son
Y el estado después de la percusión es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 12:49 8 nov 2023 |  | 312 × 336 (43 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:


















![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4a23b503f604c1368ebbf85e321e420e2f0f41)








![{\displaystyle {\overset {\leftrightarrow }{I}}_{G}\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\qquad \qquad I_{0}={\dfrac {1}{12}}m(2d)^{2}={\dfrac {1}{3}}md^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37269dc5f1c7a263239a96c2075aa35a40fb3517)



![{\displaystyle {\vec {L}}_{G}=\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\left[{\begin{array}{c}{\dot {\theta }}\\-{\dot {\phi }}\cos \theta \\{\dot {\phi }}\,\mathrm {sen} \,\theta \end{array}}\right]_{2}=\left[{\begin{array}{c}I_{0}{\dot {\theta }}\\-I_{0}{\dot {\phi }}\cos \theta \\0\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc996eec2dd249119be24488967d2e4b740e08af)

![{\displaystyle {\begin{array}{l}{\vec {\omega }}_{21}=[{\dot {\theta }},\,0,\,0]_{0}\\\\{\vec {v}}_{21}^{\,G}=[{\dot {s}},\,-d{\dot {\theta }}\,\mathrm {sen} \,\theta \,d{\dot {\theta }}\cos \theta ]_{0}\\\\{\vec {L}}_{G}=[I_{0}{\dot {\theta }},\,0,\,0]_{0}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f66aef68b890f5e57444b4706d61ebff8c40f079)














![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74504845096ff25661e04eb45d3e8c36ef687be)
![{\displaystyle {\overrightarrow {GB}}=[0,d\cos \theta ,d\,\mathrm {sen} \,\theta ]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad29b3dbd6390be8914616511de963441f031407)
![{\displaystyle {\vec {v}}_{21}^{\,B}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GB}}=[{\dot {s}},-2d{\dot {\theta }}\,\mathrm {sen} \,\theta ,2d{\dot {\theta }}\cos \theta ]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cab4d4c8dcf3ad613d4754475feefb37fdc237b4)



![{\displaystyle {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}=[1,\,0,\,0]_{0},\qquad {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}=[0,\,-2d\,\mathrm {sen} \,\theta ,\,2d\cos \theta ]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0964b443529aa4ec3893885b107b4c7376717527)
![{\displaystyle \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}\right|_{t=0}=[1,\,0,\,0]_{0},\qquad \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}\right|_{t=0}=[0,\,2d,\,0]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76703a72063ff26a36b8eb366d8a94645b578305)

