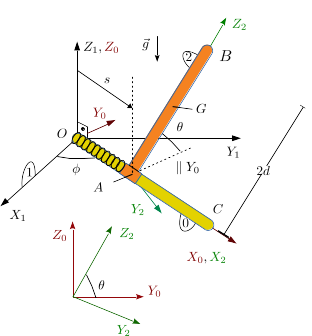
Enunciado Una barra de longitud
2
d
{\displaystyle 2d}
O
Z
1
{\displaystyle OZ_{1}}
O
{\displaystyle O}
O
X
1
Y
1
{\displaystyle OX_{1}Y_{1}}
2
d
{\displaystyle 2d}
m
{\displaystyle m}
A
{\displaystyle A}
k
{\displaystyle k}
l
0
=
d
{\displaystyle l_{0}=d}
O
{\displaystyle O}
A
{\displaystyle A}
Determina las reducciones cinemáticas
{
01
}
,
{
20
}
{\displaystyle \{01\},\{20\}}
{
21
}
{\displaystyle \{21\}}
G
{\displaystyle G}
Calcula el momento cinético de la barra "2" respecto de
G
{\displaystyle G}
A partir de ahora suponemos que
ϕ
=
ϕ
˙
=
ϕ
¨
=
0
{\displaystyle \phi ={\dot {\phi }}={\ddot {\phi }}=0}
ϕ
{\displaystyle \phi }
En
t
=
0
{\displaystyle t=0}
s
(
0
)
=
d
{\displaystyle s(0)=d}
θ
(
0
)
=
−
π
/
2
{\displaystyle \theta (0)=-\pi /2}
s
˙
(
0
)
=
0
{\displaystyle {\dot {s}}(0)=0}
θ
˙
=
0
{\displaystyle {\dot {\theta }}=0}
ϕ
{\displaystyle \phi }
F
^
→
=
[
F
^
0
,
0
,
F
^
0
]
1
{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]_{1}}
Solución Reducciones cinemáticas en
G
{\displaystyle G}
Para el movimiento {01} tenemos
ω
→
01
=
ϕ
˙
k
→
0
,
v
→
01
O
=
0
→
.
{\displaystyle {\vec {\omega }}_{01}={\dot {\phi }}\,{\vec {k}}_{0},\qquad {\vec {v}}_{01}^{\,O}={\vec {0}}.}
Teniendo en cuenta que
O
G
→
=
s
ı
→
0
+
d
cos
θ
ȷ
→
0
+
d
s
e
n
θ
k
→
0
,
{\displaystyle {\overrightarrow {OG}}=s\,{\vec {\imath }}_{0}+d\cos {\theta }\,{\vec {\jmath }}_{0}+d\,\mathrm {sen} \,\theta \,{\vec {k}}_{0},}
tenemos
v
→
01
G
=
v
→
01
O
+
ω
→
01
×
O
G
→
=
−
d
ϕ
˙
cos
θ
ı
→
0
+
s
ϕ
˙
ȷ
→
0
.
{\displaystyle {\vec {v}}_{01}^{\,G}={\vec {v}}_{01}^{\,O}+{\vec {\omega }}_{01}\times {\overrightarrow {OG}}=-d{\dot {\phi }}\cos \theta \,{\vec {\imath }}_{0}+s{\dot {\phi }}\,{\vec {\jmath }}_{0}.}
Para el movimiento {20}
ω
→
20
=
θ
˙
ı
→
0
,
v
→
01
A
=
s
˙
ı
→
0
.
{\displaystyle {\vec {\omega }}_{20}={\dot {\theta }}\,{\vec {\imath }}_{0},\qquad {\vec {v}}_{01}^{\,A}={\dot {s}}\,{\vec {\imath }}_{0}.}
Teniendo en cuenta que
A
G
→
=
d
cos
θ
ȷ
→
0
+
d
s
e
n
θ
k
→
0
,
{\displaystyle {\overrightarrow {AG}}=d\cos {\theta }\,{\vec {\jmath }}_{0}+d\,\mathrm {sen} \,\theta \,{\vec {k}}_{0},}
tenemos
v
→
20
G
=
s
˙
ı
→
0
−
d
θ
˙
s
e
n
θ
ȷ
→
0
+
d
θ
˙
cos
θ
k
→
0
.
{\displaystyle {\vec {v}}_{20}^{\,G}={\dot {s}}\,{\vec {\imath }}_{0}-d{\dot {\theta }}\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{0}+d{\dot {\theta }}\cos \theta \,{\vec {k}}_{0}.}
Para el movimiento {21} usamos las leyes de composición
ω
→
21
=
ω
→
20
+
ω
→
01
=
θ
˙
ı
→
0
+
ϕ
˙
k
→
0
.
v
→
21
G
=
v
→
20
G
+
v
→
01
G
=
(
s
˙
−
d
ϕ
˙
cos
θ
)
ı
→
0
−
d
θ
˙
s
e
n
θ
ȷ
→
0
+
d
θ
˙
cos
θ
k
→
0
.
{\displaystyle {\begin{array}{l}{\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}={\dot {\theta }}\,{\vec {\imath }}_{0}+{\dot {\phi }}\,{\vec {k}}_{0}.\\\\{\vec {v}}_{21}^{\,G}={\vec {v}}_{20}^{\,G}+{\vec {v}}_{01}^{\,G}=({\dot {s}}-d{\dot {\phi }}\cos \theta )\,{\vec {\imath }}_{0}-d{\dot {\theta }}\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{0}+d{\dot {\theta }}\cos \theta \,{\vec {k}}_{0}.\end{array}}}
Momento cinético de la barra respecto a
G
{\displaystyle G}
El momento cinético respecto al Centro de Masas
G
{\displaystyle G}
L
→
G
=
I
↔
G
⋅
ω
→
21
.
{\displaystyle {\vec {L}}_{G}={\overset {\leftrightarrow }{I}}_{G}\cdot {\vec {\omega }}_{21}.}
El tensor de inercia es
I
↔
G
[
I
0
0
0
0
I
0
0
0
0
0
]
2
I
0
=
1
12
m
(
2
d
)
2
=
1
3
m
d
2
.
{\displaystyle {\overset {\leftrightarrow }{I}}_{G}\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\qquad \qquad I_{0}={\dfrac {1}{12}}m(2d)^{2}={\dfrac {1}{3}}md^{2}.}
Hay que expresar
ω
→
21
{\displaystyle {\vec {\omega }}_{21}}
ı
→
0
=
ı
→
2
,
ȷ
→
0
=
s
e
n
θ
ȷ
→
2
+
cos
θ
k
→
2
,
k
→
0
=
−
cos
θ
ȷ
→
2
+
s
e
n
θ
k
→
2
.
{\displaystyle {\begin{array}{l}{\vec {\imath }}_{0}={\vec {\imath }}_{2},\\{\vec {\jmath }}_{0}=\mathrm {sen} \,\theta \,{\vec {\jmath }}_{2}+\cos \theta \,{\vec {k}}_{2},\\{\vec {k}}_{0}=-\cos \theta \,{\vec {\jmath }}_{2}+\mathrm {sen} \,\theta \,{\vec {k}}_{2}.\end{array}}}
Entonces
ω
→
21
=
θ
˙
ı
→
0
+
ϕ
˙
k
→
0
=
θ
˙
ı
→
2
−
ϕ
˙
cos
θ
ȷ
→
0
+
ϕ
˙
s
e
n
θ
k
→
2
.
{\displaystyle {\vec {\omega }}_{21}={\dot {\theta }}\,{\vec {\imath }}_{0}+{\dot {\phi }}\,{\vec {k}}_{0}={\dot {\theta }}\,{\vec {\imath }}_{2}-{\dot {\phi }}\cos \theta \,{\vec {\jmath }}_{0}+{\dot {\phi }}\,\mathrm {sen} \,\theta \,{\vec {k}}_{2}.}
El momento cinético es
L
→
G
=
[
I
0
0
0
0
I
0
0
0
0
0
]
2
[
θ
˙
−
ϕ
˙
cos
θ
ϕ
˙
s
e
n
θ
]
2
=
[
I
0
θ
˙
−
I
0
ϕ
˙
cos
θ
0
]
2
{\displaystyle {\vec {L}}_{G}=\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\left[{\begin{array}{c}{\dot {\theta }}\\-{\dot {\phi }}\cos \theta \\{\dot {\phi }}\,\mathrm {sen} \,\theta \end{array}}\right]_{2}=\left[{\begin{array}{c}I_{0}{\dot {\theta }}\\-I_{0}{\dot {\phi }}\cos \theta \\0\end{array}}\right]_{2}}
Ecuaciones de Lagrange Al restringir el grado de libertad
ϕ
{\displaystyle \phi }
{
s
,
θ
}
{\displaystyle \{s,\theta \}}
ω
→
21
=
[
θ
˙
,
0
,
0
]
0
v
→
21
G
=
[
s
˙
,
−
d
θ
˙
s
e
n
θ
d
θ
˙
cos
θ
]
0
L
→
G
=
[
I
0
θ
˙
,
0
,
0
]
0
.
{\displaystyle {\begin{array}{l}{\vec {\omega }}_{21}=[{\dot {\theta }},\,0,\,0]_{0}\\\\{\vec {v}}_{21}^{\,G}=[{\dot {s}},\,-d{\dot {\theta }}\,\mathrm {sen} \,\theta \,d{\dot {\theta }}\cos \theta ]_{0}\\\\{\vec {L}}_{G}=[I_{0}{\dot {\theta }},\,0,\,0]_{0}.\end{array}}}
Energía cinética Tenemos
T
=
T
t
r
a
+
T
r
o
t
{\displaystyle T=T_{tra}+T_{rot}}
Para la energía cinética de traslación
T
t
r
a
=
1
2
m
|
v
→
21
G
|
2
=
1
2
m
(
s
˙
2
+
d
2
θ
˙
2
)
.
{\displaystyle T_{tra}={\dfrac {1}{2}}m|{\vec {v}}_{21}^{\,G}|^{2}={\dfrac {1}{2}}m({\dot {s}}^{2}+d^{2}{\dot {\theta }}^{2}).}
La de rotación es
T
r
o
t
=
1
2
L
→
G
⋅
ω
→
21
=
1
6
m
d
2
θ
˙
2
.
{\displaystyle T_{rot}={\dfrac {1}{2}}{\vec {L}}_{G}\cdot {\vec {\omega }}_{21}={\dfrac {1}{6}}md^{2}{\dot {\theta }}^{2}.}
Hemos usado la expresión de
ω
→
21
{\displaystyle {\vec {\omega }}_{21}}
L
→
G
{\displaystyle {\vec {L}}_{G}}
T
=
1
6
m
(
3
s
˙
2
+
4
d
2
θ
˙
2
)
.
{\displaystyle T={\dfrac {1}{6}}m(3{\dot {s}}^{2}+4d^{2}{\dot {\theta }}^{2}).}
Energía potencial Contribuyen el muelle y la gravedad
U
g
=
m
g
d
s
e
n
θ
,
U
k
=
1
2
k
(
s
−
d
)
2
.
{\displaystyle U_{g}=mgd\,\mathrm {sen} \,\theta ,\qquad U_{k}={\dfrac {1}{2}}k(s-d)^{2}.}
Para la energía potencial gravitatoria hemos tomado como referencia el plano
O
X
1
Y
1
{\displaystyle OX_{1}Y_{1}}
U
=
U
g
+
U
k
=
m
g
d
s
e
n
θ
+
1
2
k
(
s
−
d
)
2
.
{\displaystyle U=U_{g}+U_{k}=mgd\,\mathrm {sen} \,\theta +{\dfrac {1}{2}}k(s-d)^{2}.}
Ecuaciones de Lagrange La función de Lagrange es
L
=
T
−
U
=
1
6
m
(
3
s
˙
2
+
4
d
2
θ
˙
2
)
−
m
g
d
s
e
n
θ
−
1
2
k
(
s
−
d
)
2
.
{\displaystyle L=T-U={\dfrac {1}{6}}m(3{\dot {s}}^{2}+4d^{2}{\dot {\theta }}^{2})-mgd\,\mathrm {sen} \,\theta -{\dfrac {1}{2}}k(s-d)^{2}.}
Ecuación de Lagrange para
s
{\displaystyle s}
∂
L
∂
s
˙
=
m
s
˙
,
d
d
t
(
∂
L
∂
s
˙
)
=
m
s
¨
,
∂
L
∂
s
=
−
k
(
s
−
d
)
.
}
→
s
¨
+
k
m
(
s
−
d
)
=
0
{\displaystyle \left.{\begin{array}{l}{\dfrac {\partial L}{\partial {\dot {s}}}}=m{\dot {s}},\\\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {s}}}}\right)=m{\ddot {s}},\\\\{\dfrac {\partial L}{\partial s}}=-k(s-d).\end{array}}\right\}\to {\ddot {s}}+{\dfrac {k}{m}}(s-d)=0}
Ecuación de Lagrange para
θ
{\displaystyle \theta }
∂
L
∂
θ
˙
=
4
3
m
d
2
θ
˙
,
d
d
t
(
∂
L
∂
θ
˙
)
=
4
3
m
d
2
θ
¨
,
∂
L
∂
θ
=
−
m
g
d
cos
θ
.
}
→
θ
¨
+
3
g
4
d
cos
θ
=
0.
{\displaystyle \left.{\begin{array}{l}{\dfrac {\partial L}{\partial {\dot {\theta }}}}={\dfrac {4}{3}}md^{2}{\dot {\theta }},\\\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)={\dfrac {4}{3}}md^{2}{\ddot {\theta }},\\\\{\dfrac {\partial L}{\partial \theta }}=-mgd\cos \theta .\end{array}}\right\}\to {\ddot {\theta }}+{\dfrac {3g}{4d}}\cos \theta =0.}
En este caso las dos ecuaciones están desacopladas.
Percusión El estado inicial del sistema es
s
(
0
)
=
d
,
s
˙
(
0
)
=
0
,
θ
(
0
)
=
−
π
/
2
,
θ
˙
(
0
)
=
0.
{\displaystyle s(0)=d,\qquad {\dot {s}}(0)=0,\qquad \theta (0)=-\pi /2,\qquad {\dot {\theta }}(0)=0.}
La percusión se aplica en
B
{\displaystyle B}
F
^
→
=
[
F
^
0
,
0
,
F
^
0
]
{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]}
B
{\displaystyle B}
G
B
→
=
[
0
,
d
cos
θ
,
d
s
e
n
θ
]
0
{\displaystyle {\overrightarrow {GB}}=[0,d\cos \theta ,d\,\mathrm {sen} \,\theta ]_{0}}
v
→
21
B
=
v
→
21
G
+
ω
→
21
×
G
B
→
=
[
s
˙
,
−
2
d
θ
˙
s
e
n
θ
,
2
d
θ
˙
cos
θ
]
0
.
{\displaystyle {\vec {v}}_{21}^{\,B}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GB}}=[{\dot {s}},-2d{\dot {\theta }}\,\mathrm {sen} \,\theta ,2d{\dot {\theta }}\cos \theta ]_{0}.}
Los momentos generalizados son
p
s
=
∂
L
∂
s
˙
=
m
s
˙
,
p
θ
=
∂
L
∂
θ
˙
=
4
3
m
d
2
θ
˙
.
{\displaystyle p_{s}={\dfrac {\partial L}{\partial {\dot {s}}}}=m{\dot {s}},\qquad p_{\theta }={\dfrac {\partial L}{\partial {\dot {\theta }}}}={\dfrac {4}{3}}md^{2}{\dot {\theta }}.}
Las ecuaciones de Lagrange impulsivas son
Δ
p
s
=
Q
^
s
N
C
=
F
^
→
⋅
∂
v
→
21
B
∂
s
˙
|
t
=
0
,
Δ
p
θ
=
Q
^
s
N
C
=
F
^
→
⋅
∂
v
→
21
B
∂
θ
˙
|
t
=
0
.
{\displaystyle {\begin{array}{l}\Delta p_{s}={\hat {Q}}_{s}^{NC}=\left.{\vec {\hat {F}}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}\right|_{t=0},\\\\\Delta p_{\theta }={\hat {Q}}_{s}^{NC}=\left.{\vec {\hat {F}}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}\right|_{t=0}.\end{array}}}
Como se parte del reposo
Δ
p
s
=
m
s
˙
+
,
Δ
p
θ
=
4
3
m
d
2
θ
˙
+
.
{\displaystyle \Delta p_{s}=m{\dot {s}}^{+},\qquad \Delta p_{\theta }={\dfrac {4}{3}}md^{2}{\dot {\theta }}^{+}.}
Tenemos
∂
v
→
21
B
∂
s
˙
=
[
1
,
0
,
0
]
0
,
∂
v
→
21
B
∂
θ
˙
=
[
0
,
−
2
d
s
e
n
θ
,
2
d
cos
θ
]
0
.
{\displaystyle {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}=[1,\,0,\,0]_{0},\qquad {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}=[0,\,-2d\,\mathrm {sen} \,\theta ,\,2d\cos \theta ]_{0}.}
Por tanto
∂
v
→
21
B
∂
s
˙
|
t
=
0
=
[
1
,
0
,
0
]
0
,
∂
v
→
21
B
∂
θ
˙
|
t
=
0
=
[
0
,
2
d
,
0
]
0
.
{\displaystyle \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}\right|_{t=0}=[1,\,0,\,0]_{0},\qquad \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}\right|_{t=0}=[0,\,2d,\,0]_{0}.}
Las percusiones generalizadas son
Q
s
N
C
=
F
^
0
,
Q
θ
N
C
=
0.
{\displaystyle Q_{s}^{NC}={\hat {F}}_{0},\qquad Q_{\theta }^{NC}=0.}
Y el estado después de la percusión es
s
˙
(
0
+
)
=
F
^
0
m
,
θ
˙
(
0
+
)
=
0.
{\displaystyle {\dot {s}}(0^{+})={\dfrac {{\hat {F}}_{0}}{m}},\qquad {\dot {\theta }}(0^{+})=0.}


















![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4a23b503f604c1368ebbf85e321e420e2f0f41)








![{\displaystyle {\overset {\leftrightarrow }{I}}_{G}\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\qquad \qquad I_{0}={\dfrac {1}{12}}m(2d)^{2}={\dfrac {1}{3}}md^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37269dc5f1c7a263239a96c2075aa35a40fb3517)



![{\displaystyle {\vec {L}}_{G}=\left[{\begin{array}{ccc}I_{0}&0&0\\0&I_{0}&0\\0&0&0\end{array}}\right]_{2}\left[{\begin{array}{c}{\dot {\theta }}\\-{\dot {\phi }}\cos \theta \\{\dot {\phi }}\,\mathrm {sen} \,\theta \end{array}}\right]_{2}=\left[{\begin{array}{c}I_{0}{\dot {\theta }}\\-I_{0}{\dot {\phi }}\cos \theta \\0\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc996eec2dd249119be24488967d2e4b740e08af)

![{\displaystyle {\begin{array}{l}{\vec {\omega }}_{21}=[{\dot {\theta }},\,0,\,0]_{0}\\\\{\vec {v}}_{21}^{\,G}=[{\dot {s}},\,-d{\dot {\theta }}\,\mathrm {sen} \,\theta \,d{\dot {\theta }}\cos \theta ]_{0}\\\\{\vec {L}}_{G}=[I_{0}{\dot {\theta }},\,0,\,0]_{0}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f66aef68b890f5e57444b4706d61ebff8c40f079)














![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74504845096ff25661e04eb45d3e8c36ef687be)
![{\displaystyle {\overrightarrow {GB}}=[0,d\cos \theta ,d\,\mathrm {sen} \,\theta ]_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad29b3dbd6390be8914616511de963441f031407)
![{\displaystyle {\vec {v}}_{21}^{\,B}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GB}}=[{\dot {s}},-2d{\dot {\theta }}\,\mathrm {sen} \,\theta ,2d{\dot {\theta }}\cos \theta ]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cab4d4c8dcf3ad613d4754475feefb37fdc237b4)



![{\displaystyle {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}=[1,\,0,\,0]_{0},\qquad {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}=[0,\,-2d\,\mathrm {sen} \,\theta ,\,2d\cos \theta ]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0964b443529aa4ec3893885b107b4c7376717527)
![{\displaystyle \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {s}}}}\right|_{t=0}=[1,\,0,\,0]_{0},\qquad \left.{\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}\right|_{t=0}=[0,\,2d,\,0]_{0}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76703a72063ff26a36b8eb366d8a94645b578305)

