Disco rodando sobre escuadra giratoria
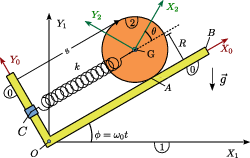
Un disco (sólido "2") de masa y radio , rueda sin deslizar sobre una escuadra (sólido "0") de masa despreciable. La escuadra gira en el plano con velocidad angular constante .
- Encuentra reducciones cinemáticas de todos los movimientos del problema en el centro del disco .
- Calcula el momento cinético del disco respecto a y , su energía cinética y su energía potencial.
- Aplicando los métodos de la Mecánica Vectorial, encuentra las ecuaciones de movimiento del disco. ¿Cuál es la frecuencia propia de oscilación del sistema (también llamada frecuencia natural)?
- Encuentra las fuerzas y momentos que actúan sobre la escuadra (sólido "0") para que se mueva de la forma descrita.
Barra rotando alrededor de barra horizontal con muelle
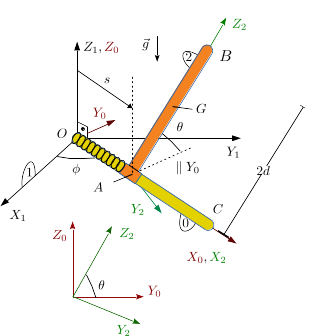
Una barra de longitud y masa despreciable (sólido "0") puede rotar alrededor del eje . El punto de la barra es fijo. La barra "0" siempre está contenida en el plano . Otra barra, también de longitud y masa (sólido "2"), está conectada a la barra "0" por un pasador en el punto . El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica y longitud natural nula conecta los puntos y .
- Determina las reducciones cinemáticas y en .
- Calcula el momento cinético de la barra "2" respecto de .
- A partir de ahora suponemos que , es decir, la coordenada ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema.
- En tenemos , , y ( sigue estando fijada). La barra "2" recibe una percusión en el punto B. Determina el estado del sistema justo después de la percusión.





















![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4a23b503f604c1368ebbf85e321e420e2f0f41)