(Página creada con «= Enunciado = right Una cuerda ideal sin masa está completamente enrollada en una polea de masa <math>M=2m</math> y radio <math>R</math>. Al extremo de la cuerda está atada una masa <math>m</math>. El centro de la polea, que es un punto fijo, se encuentra a una altura <math>H</math> del suelo. En el instante inicial la masa estaba a la altura del centro de la polea (punto <math>A</math> de la figura) y la polea estaba en…»)
 
(Página creada con «== Tiro parabólico con plano inclinado == right|350px Se tiene el plano inclinado de la figura que forma un ángulo <math>\theta</math> con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial <math>\vec{v}_0</math>, de módulo <math>10v_p</math> y con un ángulo <math>\alpha</math> con la horizontal. Los ángulos son t…»)
 
Línea 1: Línea 1:
= Enunciado =
==[[ Tiro parabólico con plano inclinado, Septiembre 2019 (G.I.E.R.M.)| Tiro parabólico con plano inclinado ]]==
[[File:F1GIERM_polea_masa_enunciado.png|right]]
[[Archivo:F1GIC-particula-rampa.png|right|350px]]
Una cuerda ideal sin masa está completamente enrollada en una polea de masa <math>M=2m</math> y radio <math>R</math>. Al extremo de la
Se tiene el plano inclinado de la figura que forma un ángulo <math>\theta</math> con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial <math>\vec{v}_0</math>, de módulo <math>10v_p</math> y con un ángulo <math>\alpha</math> con la horizontal. Los ángulos son tales que
cuerda está atada una masa <math>m</math>.  El centro de la polea, que es un punto fijo, se encuentra a una altura <math>H</math> del suelo.
En el instante inicial la masa estaba a la altura del centro de la polea
(punto <math>A</math> de la figura) y la polea estaba en reposo. Entonces, se deja girar libremente a la polea.
La gravedad actúa como se indica en la figura. Supondremos que la cuerda está siempre tensa y que la
masa se mueve verticalmente. El momento de inercia de un disco de masa <math>M</math> y radio <math>R</math> respecto a un eje perpendicular a él que
pasa por su centro es <math>I=MR^2/2</math>.
 
#Usando la conservación de Energía Mecánica, calcula la rapidez con la que la masa impacta en el suelo.
#Dibuja el diagrama de fuerzas que actúan sobre la masa y la polea.
#Aplicando la Segunda Ley de Newton. el T.C.M. y el T.M.C, calcula la aceleración de la masa, la tensión de la cuerda y las fuerzas sobre la polea durante el movimiento.
 
= Solución =
 
== Impacto con el suelo ==
La única fuerza que hace trabajo es la gravedad. Al ser conservativa, se conserva la energía mecánica. Pero hay que tener en cuenta '''la energía cinética de la polea''', pues tiene masa.
 
Tomando como referencia de energía potencial el suelo, en el instante inicial la energía mecánica es puramente potencial gravitatoria
<center>
<math>
E = mgH + MgH = 3mgH.
</math>
</center>
Cuando la masa <math>m</math> impacta con el suelo la energía mecánica consta de la energía cinética y la energía pontencial gravitatoria de la polea
<center>
<center>
<math>
<math>
E = T + MgH.
\mathrm{sen}\,\theta = \dfrac{3}{5}\qquad \cos\theta=\dfrac{4}{5} \qquad\qquad\qquad
</math>
\mathrm{sen}\,\alpha= \dfrac{4}{5}\qquad \cos\alpha=\dfrac{3}{5}.
</center>
La energía cinética es la suma de las energías cinéticas de la masa, <math>T_m</math> y de la polea, <math>T_M</math>
<center>
<math>
\begin{array}{l}
T_m = \dfrac{1}{2}mv_m^2, \\
\\
T_M = \dfrac{1}{2}I\omega^2 = \dfrac{1}{2}\dfrac{2mR^2}{2}\dfrac{v_m^2}{R^2} =  
\dfrac{1}{2}mv_m^2.
\end{array}
</math>
</center>
Hemos usado que <math>\omega=v_m/R</math>, pues la velocidad de la masa es en todo instante
igual a la del punto <math>A</math> de la polea. Entonces, la energía mecánica del sistema
cuando la masa impacta con el suelo es
<center>
<math>
E = T_m + T_M + MgH = mv_m^2 + 2mgH.
</math>
</center>
Igualando con el valor inicial de la energía mecánica tenemos
<center>
<math>
3mgH = mv_m^2 + 2mg \Longrightarrow v_m = \sqrt{gH}.
</math>
</math>
</center>
</center>


== Diagrama de fuerzas ==
[[File:F1GIERM_polea_masa_fuerzas.png|right]]
El diagrama de la derecha muestra las fuerzas que actúan sobre la masa y la polea. Sobre la masa actúan el peso y la tensión de la cuerda. Sobre la polea son su peso, la tensión de la cuerda en <math>A</math> y la fuerza vincular en <math>O</math> que garantiza que este punto nose mueve.
La expresión de estas fuerzas en el sistema de ejes de la figura es, para la masa <math>m</math>
<center>
<math>
\begin{array}{l}
\vec{P}_m = mg\,\vec{\imath}, \\
\vec{T}_m = -T\,\vec{\imath}.
\end{array}
</math>
</center>
Para la polea tenemos
<center>
<math>
\begin{array}{l}
\vec{P}_M = Mg\,\vec{\imath}, \\
\vec{T}_A = T\,\vec{\imath}, \\
\vec{O} = O_x\,\vec{\imath} + O_y\,\vec{\jmath}.
\end{array}
</math>
</center>
Como la cuerda no tiene masa tenemos <math>\vec{T}_A = -\vec{T}_m</math>. La fuerza <math>\vec{O}</math> tiene dos componentes a priori no nulas pues el punto <math>O</math> tiene dos movimientos prohibidos, en las direcciones de los ejes.


== Aplicación de los Teoremas Fundamentales ==
#Calcula la distancia <math>l</math> entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
Hemos de aplicar la Segunda Ley de Newton a la masa y el T.C.M. y el T.M.C. a la polea. Para la masa tenemos
#Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos <math>O</math> y <math>A</math>.  
<center>
#Calcula la potencia que la gravedad transmite a la partícula en cada. Discute el significado físico del signo de esta potencia.
<math>
#Calcula las componentes intrínsecas de la aceleración en el punto de impacto.
m\vec{a}_m = \vec{P}_m + \vec{T}_m
\Longrightarrow
ma = mg - T. \qquad (1)
</math>
</center>
Aplicando el T.C.M. a la polea tenemos
<center>
<math>
m\vec{a}_O = \vec{P}_M + \vec{T}_A + \vec{O}.
</math>
</center>
El centro de masas de la polea no se mueve, <math>\vec{a}_O=\vec{0}</math>. Obtenemos así
dos ecuaciones
<center>
<math>
\begin{array}{lr}
Mg + T + O_x = 0, & (2)\\
O_y = 0. & (3)
\end{array}
</math>
</center>
Aplicamos el T.M.C. en el centro de la polea. La única fuerza que crea momento en este caso es <math>\vec{T}_A</math>
<center>
<math>
\dot{\vec{L}}_O = \overrightarrow{OA}\times\vec{T}_A.
</math>
</center>
El momento cinético es
<center>
<math>
\vec{L}_O = I\vec{\omega}.
</math>
</center>
Su derivada temporal es
<center>
<math>
\dot{\vec{L}}_O = I\vec{\alpha} = I\alpha\,\vec{k}.
</math>
</center>
La aceleración tangencial del punto <math>A</math> de la polea coincide con la aceleración del punto <math>A</math> de la cuerda y, por tanto, con la aceleración de la masa
<center>
<math>
\alpha = a/R \Longrightarrow \dot{\vec{L}}_O = I\dfrac{a}{R}\,\vec{k} = mRa\,\vec{k}.
</math>
</center>
El momento creado por la fuerza es
<center>
<math>
\overrightarrow{OA}\times\vec{T}_A = (-R\,\vec{\jmath})\times(T\,\vec{\imath})
= RT\,\vec{k}.
</math>
</center>
El T.M.C. nos da entonces la ecuación
<center>
<math>
ma = T. \qquad (4)
</math>
</center>
Tenemos cuatro incógnitas: <math>\{a, T, O_x, O_y\} </math> con cuatro ecuaciones.
Resolviendo llegamos a
<center>
<math>
a = \dfrac{1}{2}g, \qquad T = \dfrac{1}{2}mg, \qquad O_x = -\dfrac{5}{2}mg, \qquad O_y = 0.
</math>
</center>
La aceleración de la masa y las fuerzas sobre la polea son
<center>
<math>
\vec{a}_m = \dfrac{1}{2}g\,\vec{\imath}, \qquad
\vec{T}_A = \dfrac{1}{2}mg\,\vec{\imath}, \qquad
\vec{O} = -\dfrac{5}{2}mg\,\vec{\imath}, \qquad
\vec{P}_M = 2mg\,\vec{\imath}.
</math>
</center>


== Errores comunes detectados durante la corrección ==
==[[ Barra rotando con disco, Septiembre 2019 (G.I.E.R.M.)| Barra rotando con disco ]]==
#Al aplicar la conservación de Energía Mecánica hay que tener en cuenta la energía cinética de rotación de la polea.
[[File:F1GIERM_barra_disco_enunciado.png|right]]
#No hay que confundir la aceleración de la masa con la del centro de la polea. Ésta última es nula.
Una varilla recta y rígida (sólido "0") se mueve siempre contenida en el plano
#El T.C.M. y el T.M.C. se aplican sólo a la polea. No hay que incluir el momento angular de la masa ni el momento de fuerza creado por su peso.
fijo <math>OX_1Y_1</math> (sólido "1"), girando, con velocidad angular constante <math>\Omega</math>
y en el sentido indicado en la figura, alrededor de su extremo articulado el
punto fijo <math>O</math>. El centro <math>C</math> de un disco de radio <math>R</math> (sólido "2"), recorre
la varilla alejándose con aceleración constante <math>2a_0</math>. En el instante inicial
<math>t=0</math>, el punto <math>C</math> coincidía con el <math>O</math> y su velocidad era nula.
A su vez, el disco gira
alrededor de su centro <math>C</math> en el sentido indicado, con velocidad angular
constante <math>\omega</math> (respecto a la varilla) y permaneciendo siempre paralelo al
plano fijo <math>OX_1Y_1</math>. En el instante inicial la varilla recta
coincidía con el eje <math>OX_1</math>,


[[Categoría:Problemas de dinámica del sólido rígido]]
#Determina reducciones cinemáticas y sus derivadas temporales de los movimientos {01}, {20} y {21}. Puedes hacerlo en cualquier punto.
[[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]]
#En el instante <math>t=1/\Omega</math>, encuentra la posición de los C.I.R. de los tres movimientos.
[[Categoría:Física I (G.I.E.R.M.)]]

Revisión actual - 14:39 31 oct 2023

Tiro parabólico con plano inclinado

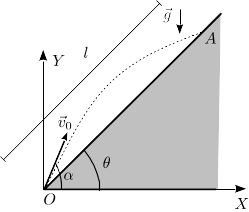
Se tiene el plano inclinado de la figura que forma un ángulo con la horizontal. Se dispara una partícula desde el punto más bajo, con una velocidad inicial , de módulo y con un ángulo con la horizontal. Los ángulos son tales que


  1. Calcula la distancia entre el punto de partida y el de impacto sobre el plano inclinado, así como la velocidad (vector) con la que impacta.
  2. Calcula el trabajo realizado por la fuerza gravitatoria sobre la partícula entre los puntos y .
  3. Calcula la potencia que la gravedad transmite a la partícula en cada. Discute el significado físico del signo de esta potencia.
  4. Calcula las componentes intrínsecas de la aceleración en el punto de impacto.

Barra rotando con disco

Una varilla recta y rígida (sólido "0") se mueve siempre contenida en el plano fijo (sólido "1"), girando, con velocidad angular constante y en el sentido indicado en la figura, alrededor de su extremo articulado el punto fijo . El centro de un disco de radio (sólido "2"), recorre la varilla alejándose con aceleración constante . En el instante inicial , el punto coincidía con el y su velocidad era nula. A su vez, el disco gira alrededor de su centro en el sentido indicado, con velocidad angular constante (respecto a la varilla) y permaneciendo siempre paralelo al plano fijo . En el instante inicial la varilla recta coincidía con el eje ,

  1. Determina reducciones cinemáticas y sus derivadas temporales de los movimientos {01}, {20} y {21}. Puedes hacerlo en cualquier punto.
  2. En el instante , encuentra la posición de los C.I.R. de los tres movimientos.
Obtenido de «http://laplace.us.es/wiki/index.php?title=Polea_con_masa,_Enero_2019_(G.I.E.R.M.)&oldid=1248»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Polea_con_masa,_Enero_2019_(G.I.E.R.M.)&oldid=1248»