Polea con masa, Enero 2019 (G.I.E.R.M.)

Enunciado

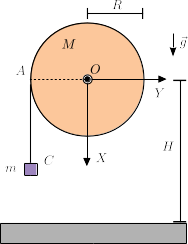
Una cuerda ideal sin masa está completamente enrollada en una polea de masa $M=2m$ y radio $R$. Al extremo de la cuerda está atada una masa $m$. El centro de la polea, que es un punto fijo, se encuentra a una altura $H$ del suelo. En el instante inicial la masa estaba a la altura del centro de la polea (punto $A$ de la figura) y la polea estaba en reposo. Entonces, se deja girar libremente a la polea. La gravedad actúa como se indica en la figura. Supondremos que la cuerda está siempre tensa y que la masa se mueve verticalmente. El momento de inercia de un disco de masa $M$ y radio $R$ respecto a un eje perpendicular a él que pasa por su centro es $I=MR^{2}/2$.

1. Usando la conservación de Energía Mecánica, calcula la rapidez con la que la masa impacta en el suelo.
2. Dibuja el diagrama de fuerzas que actúan sobre la masa y la polea.
3. Aplicando la Segunda Ley de Newton. el T.C.M. y el T.M.C, calcula la aceleración de la masa, la tensión de la cuerda y las fuerzas sobre la polea durante el movimiento.

Solución

Impacto con el suelo

La única fuerza que hace trabajo es la gravedad. Al ser conservativa, se conserva la energía mecánica. Pero hay que tener en cuenta la energía cinética de la polea, pues tiene masa.

Tomando como referencia de energía potencial el suelo, en el instante inicial la energía mecánica es puramente potencial gravitatoria

$E=mgH+MgH=3mgH.$

Cuando la masa $m$ impacta con el suelo la energía mecánica consta de la energía cinética y la energía pontencial gravitatoria de la polea

$E=T+MgH.$

La energía cinética es la suma de las energías cinéticas de la masa, $T_{m}$ y de la polea, $T_{M}$

${\begin{array}{l}T_{m}={\dfrac {1}{2}}mv_{m}^{2},\\\\T_{M}={\dfrac {1}{2}}I\omega ^{2}={\dfrac {1}{2}}{\dfrac {2mR^{2}}{2}}{\dfrac {v_{m}^{2}}{R^{2}}}={\dfrac {1}{2}}mv_{m}^{2}.\end{array}}$

Hemos usado que $\omega =v_{m}/R$, pues la velocidad de la masa es en todo instante igual a la del punto $A$ de la polea. Entonces, la energía mecánica del sistema cuando la masa impacta con el suelo es

$E=T_{m}+T_{M}+MgH=mv_{m}^{2}+2mgH.$

Igualando con el valor inicial de la energía mecánica tenemos

$3mgH=mv_{m}^{2}+2mg\Longrightarrow v_{m}={\sqrt {gH}}.$

Diagrama de fuerzas

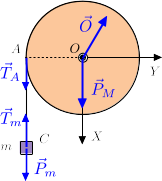
El diagrama de la derecha muestra las fuerzas que actúan sobre la masa y la polea. Sobre la masa actúan el peso y la tensión de la cuerda. Sobre la polea son su peso, la tensión de la cuerda en $A$ y la fuerza vincular en $O$ que garantiza que este punto nose mueve.

La expresión de estas fuerzas en el sistema de ejes de la figura es, para la masa $m$

${\begin{array}{l}{\vec {P}}_{m}=mg\,{\vec {\imath }},\\{\vec {T}}_{m}=-T\,{\vec {\imath }}.\end{array}}$

Para la polea tenemos

${\begin{array}{l}{\vec {P}}_{M}=Mg\,{\vec {\imath }},\\{\vec {T}}_{A}=T\,{\vec {\imath }},\\{\vec {O}}=O_{x}\,{\vec {\imath }}+O_{y}\,{\vec {\jmath }}.\end{array}}$

Como la cuerda no tiene masa tenemos ${\vec {T}}_{A}=-{\vec {T}}_{m}$. La fuerza ${\vec {O}}$ tiene dos componentes a priori no nulas pues el punto $O$ tiene dos movimientos prohibidos, en las direcciones de los ejes.

Aplicación de los Teoremas Fundamentales

Hemos de aplicar la Segunda Ley de Newton a la masa y el T.C.M. y el T.M.C. a la polea. Para la masa tenemos

$m{\vec {a}}_{m}={\vec {P}}_{m}+{\vec {T}}_{m}\Longrightarrow ma=mg-T.\qquad (1)$

Aplicando el T.C.M. a la polea tenemos

$m{\vec {a}}_{O}={\vec {P}}_{M}+{\vec {T}}_{A}+{\vec {O}}.$

El centro de masas de la polea no se mueve, ${\vec {a}}_{O}={\vec {0}}$. Obtenemos así dos ecuaciones

${\begin{array}{lr}Mg+T+O_{x}=0,&(2)\\O_{y}=0.&(3)\end{array}}$

Aplicamos el T.M.C. en el centro de la polea. La única fuerza que crea momento en este caso es ${\vec {T}}_{A}$

${\dot {\vec {L}}}_{O}={\overrightarrow {OA}}\times {\vec {T}}_{A}.$

El momento cinético es

${\vec {L}}_{O}=I{\vec {\omega }}.$

Su derivada temporal es

${\dot {\vec {L}}}_{O}=I{\vec {\alpha }}=I\alpha \,{\vec {k}}.$

La aceleración tangencial del punto $A$ de la polea coincide con la aceleración del punto $A$ de la cuerda y, por tanto, con la aceleración de la masa

$\alpha =a/R\Longrightarrow {\dot {\vec {L}}}_{O}=I{\dfrac {a}{R}}\,{\vec {k}}=mRa\,{\vec {k}}.$

El momento creado por la fuerza es

${\overrightarrow {OA}}\times {\vec {T}}_{A}=(-R\,{\vec {\jmath }})\times (T\,{\vec {\imath }})=RT\,{\vec {k}}.$

El T.M.C. nos da entonces la ecuación

$ma=T.\qquad (4)$

Tenemos cuatro incógnitas: $\{a,T,O_{x},O_{y}\}$ con cuatro ecuaciones. Resolviendo llegamos a

$a={\dfrac {1}{2}}g,\qquad T={\dfrac {1}{2}}mg,\qquad O_{x}=-{\dfrac {5}{2}}mg,\qquad O_{y}=0.$

La aceleración de la masa y las fuerzas sobre la polea son

${\vec {a}}_{m}={\dfrac {1}{2}}g\,{\vec {\imath }},\qquad {\vec {T}}_{A}={\dfrac {1}{2}}mg\,{\vec {\imath }},\qquad {\vec {O}}=-{\dfrac {5}{2}}mg\,{\vec {\imath }},\qquad {\vec {P}}_{M}=2mg\,{\vec {\imath }}.$

Errores comunes detectados durante la corrección

1. Al aplicar la conservación de Energía Mecánica hay que tener en cuenta la energía cinética de rotación de la polea.
2. No hay que confundir la aceleración de la masa con la del centro de la polea. Ésta última es nula.
3. El T.C.M. y el T.M.C. se aplican sólo a la polea. No hay que incluir el momento angular de la masa ni el momento de fuerza creado por su peso.