Segunda Convocatoria 2023/24 (G.I.C.)

Juego con bola y caja

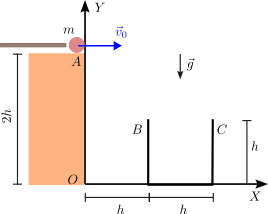
La figura ilustra un juego muy simple. Se trata de golpear una bola de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} con un taco en reposo en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t=0} , de modo que, justo después del impacto, se mueve con velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0} horizontal, como se muestra en la figura. Después del impacto, la bola se mueve en caída libre, con rozamiento del aire despreciable. Se gana en el juego si se consigue que la bola entre en la caja Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle BC} de la figura. En lo que sigue, modelaremos la bola como una partícula puntual de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} .

1. Escribe las expresiones de los vectores Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}(t)} y ${\vec {r}}(t)$ que describen la posición de la bola en cada instante de tiempo.
2. Encuentra el instante de tiempo, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t_h} , para el cual la distancia de la bola al suelo (el eje OX) es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle h} .
3. Encuentra que condiciones debe cumplir Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle |\vec{v}_0|} para ganar el juego.
4. Si la velocidad de salida de la partícula es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v_0 = 1.0\,\mathrm{m/s}} , y su masa es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m=1.00\,\mathrm{kg}} , ¿cuál es el impulso mecánico impartido por el taco a la partícula?

Masas en plano inclinado con cuerda tirando

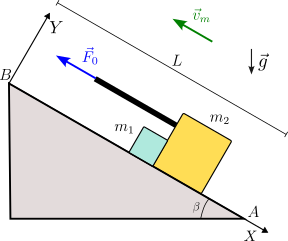
Dos masas, $m_{1}$ y $m_{2}$, deslizan sobre un plano inclinado un ángulo $\beta$ con la horizontal. El contacto entre las masas y el plano inclinado es liso. Una cuerda tensa ejerce una fuerza ${\vec {F}}_{0}=-F_{0}\,{\vec {\imath }}$ ($F_{0}>0$) sobre la masa 2, como se indica en la figura. Las masas se desplazan siempre juntas hacia arriba, con velocidad constante ${\vec {v}}_{m}=-5v_{0}\,{\vec {\imath }}$ ($v_{0}>0$). Las masas son $m_{1}=5m_{0}$, $m_{2}=10m_{0}$. Las dos masas se tratan como partículas puntuales. La longitud de la rampa del plano inclinado es $L=5L_{0}$. El ángulo $\beta$ verifica

$\mathrm {sen} \,\beta =4/5,\qquad \cos \beta =3/5.$

1. Dibuja el diagrama de fuerzas para la masas. Hazlo por separado para cada una de ellas.
2. Calcula el valor de $F_{0}$ y de la fuerza entre las masas.
3. Si en el instante inicial las dos masas estaban en el punto $A$, ¿cuál es la variación de su energía mecánica cuando llegan al punto $B$?
4. Si $L_{0}=1.00\,\mathrm {m}$, $F_{0}=100\,\mathrm {N}$, y $v_{0}=5.00\,\mathrm {m/s}$, ¿cuanto vale la potencia que ${\vec {F}}_{0}$ transmite a las masas? ¿Y el trabajo realizado por ${\vec {F}}_{0}$ entre los puntos $A$ y $B$?

Barra articulada apoyada sobre una pared

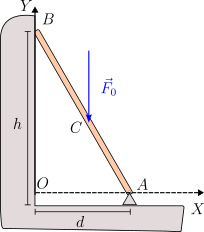
Una barra de masa despreciable está articulada en un soporte fijo en el punto $A$. Su otro extremo $B$ se apoya en una pared vertical lisa. Una fuerza conocida ${\vec {F}}_{0}=-F_{0}\,{\vec {\jmath }}$ ($F_{0}>0$) se aplica en el punto central de la barra.

1. Dibuja del diagrama de cuerpo libre de la barra.
2. Encuentra la expresión de todas las fuerzas que actúan sobre la barra cuando está en equilibrio estático.
3. Ahora se aplica sobre la barra un momento de fuerza conocido ${\vec {\tau }}=-\tau _{0}\,{\vec {k}}$ ($\tau _{0}>0$). ¿Cuál es el valor mínimo de $\tau _{0}$ para que la barra se separe de la pared en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} ?
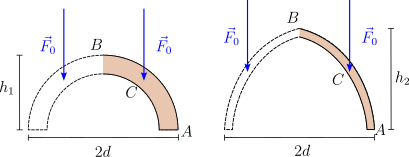
4. Este sistema se puede usar como modelo muy simple de las fuerzas sobre un arco románico y gótico. A partir del resultado del apartado 2, ¿como explicarías que la invención del arco gótico (el de la derecha) ayudó a construir edificios mas altos y con paredes mas delgadas?

Colapso de una estrella

Cuando una estrella agota el combustible que mantiene su proceso interno de fusión nuclear, es incapaz de vencer el efecto de la gravedad e implosiona, disminuyendo su radio. En el caso de una estrella como nuestro Sol al final del proceso queda una enana blanca. Supondremos que durante este proceso la estrella es un sistema aislado, de modo que no hay ninguna fuerza ni momento de fuerza externo actuando sobre ella. Supondremos también que la masa de la estrella no cambia en el proceso, y que su forma es siempre esférica.

1. Calcula el cambio de la velocidad angular de rotación de la estrella en el proceso, y por qué cambia.
2. Supongamos que tenemos una estrella similar a nuestro Sol, de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m_S = 2.00\times10^{30}\,\mathrm{kg}} y radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R_S = 7.00\times10^8\,\mathrm{m}} . Su período de rotación es de 30 días. Si el radio de la enana blanca final es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R_b=7000\, \mathrm{km}} , ¿cuál es su velocidad angular de rotación final? ¿Y el período de rotación?

Dato: El momento de inercia de una esfera maciza de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R} y masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle M} alrededor de un eje que pase por su centro es $I=2MR^{2}/5$.