Barra articulada apoyada sobre una pared, Junio 2024 (G.I.C.)

Enunciado

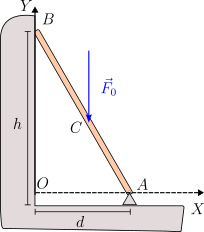
Una barra de masa despreciable está articulada en un soporte fijo en el punto $A$. Su otro extremo $B$ se apoya en una pared vertical lisa. Una fuerza conocida ${\vec {F}}_{0}=-F_{0}\,{\vec {\jmath }}$ ($F_{0}>0$) se aplica en el punto central de la barra. La altura del soporte del punto $A$ es despreciable.

1. Dibuja del diagrama de cuerpo libre de la barra.
2. Encuentra la expresión de todas las fuerzas que actúan sobre la barra cuando está en equilibrio estático.
3. Ahora se aplica sobre la barra un momento de fuerza conocido ${\vec {\tau }}=-\tau _{0}\,{\vec {k}}$ ($\tau _{0}>0$). ¿Cuál es el valor mínimo de $\tau _{0}$ para que la barra se separe de la pared en el punto $B$?
4. Este sistema se puede usar como modelo muy simple de las fuerzas sobre un arco románico y gótico. A partir del resultado del apartado 2, ¿como explicarías que la invención del arco gótico (el de la derecha) ayudó a construir edificios mas altos y con paredes mas delgadas?

Diagrama de cuerpo libre

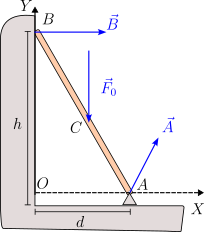
En ese problema, la posición de la barra está fijada, no es una incógnita. Las incógnitas son las fuerzas de reacción que actúan sobre la barra.

La figura de la izquierda muestra las fuerzas que actúan sobre la barra. Tratamos el problema como un sistema plano. Dado que su masa es despreciable, su peso no se tiene en cuenta. Como el contacto en el punto $B$ es liso, la fuerza de reacción en él es perpendicular a la superficie. La barra está articulada en el punto $A$, es decir, los dos movimientos posibles del extremo de la barra están prohibidos. Por tanto, la fuerza vincular tiene dos componentes. Aquí no hay fuerza normal. Como es un sólido plano sometido a tres fuerzas, podemos aplicar el teorema de las tres fuerzas. Esto se refleja en el hecho de que, para que haya equilibrio, es condición necesaria (aunque no suficiente) que las rectas soportes de las tres fuerzas se crucen en un punto. Las direcciones de la normal en B y la fuerza ${\vec {F}}_{0}$ son conocidas. Por tanto, la dirección de la fuerza ${\vec {A}}$ tiene que ser la indicada en la figura. Y el sentido debe ser el que muestra el dibujo, para que la suma vectorial de fuerzas sea cero.

Las expresiones de las fuerzas son

${\begin{array}{l}{\vec {F}}_{0}=-F_{0}\,{\vec {\jmath }},\\{\vec {B}}=B\,{\vec {\imath }},\\{\vec {A}}=A_{x}\,{\vec {\imath }}+A_{y}\,{\vec {\jmath }}.\end{array}}$

Fuerzas sobre la barra

Tenemos tres incógnitas, a saber, $\{B,A_{x},A_{y}\}$. Obtenemos las ecuaciones necesarias aplicando las condiciones de equilibrio estático: sumatorio de fuerzas y momentos nulos.

Imponiendo que la suma de fuerzas es nula tenemos

${\vec {F}}_{0}+{\vec {B}}+{\vec {A}}={\vec {0}}\Longrightarrow \left\{{\begin{array}{lclr}X)&\to &A_{x}+B=0,&(1)\\Y)&\to &A_{y}-F_{0}=0,&(2)\end{array}}\right.$

Calculamos los momentos respecto del punto $A$.

${\vec {M}}_{A}={\overrightarrow {OB}}\times {\vec {B}}+{\overrightarrow {OC}}\times {\vec {F}}_{0}={\vec {0}}.\qquad (3)$

Los vectores geométricos son

${\begin{array}{l}{\overrightarrow {OB}}=-d\,{\vec {\imath }}+h\,{\vec {\jmath }},\\\\{\overrightarrow {OC}}={\dfrac {1}{2}}{\overrightarrow {OB}}=-{\dfrac {1}{2}}d\,{\vec {\imath }}+{\dfrac {1}{2}}h\,{\vec {\jmath }}.\end{array}}$

Los productos vectoriales son

${\begin{array}{l}{\overrightarrow {OB}}\times {\vec {B}}=-Bh\,{\vec {k}},\\\\{\overrightarrow {OC}}\times {\vec {F}}_{0}={\dfrac {1}{2}}F_{0}d\,{\vec {k}}.\end{array}}$

Con lo que la ecuación (3) nos da

$-Bh+{\dfrac {1}{2}}F_{0}d=0.\qquad (4)$

Resolviendo las ecuaciones (1), (2) y (4) obtenemos

${\begin{array}{l}{\vec {A}}=-{\dfrac {F_{0}d}{2h}}\,{\vec {\imath }}+F_{0}\,{\vec {\jmath }},\\{\vec {B}}={\dfrac {F_{0}d}{2h}}\,{\vec {\imath }}.\end{array}}$

Aplicación de un momento de fuerzas externo

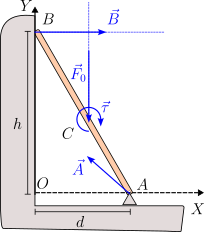
La figura de la derecha muestra el diagrama de fuerzas y momentos sobre la barra. Nótese que ahora no se cumple teorema de las tres fuerzas, debido a la presencia del momento externo. La expresión de las fuerzas en A y en B es la misma del apartado anterior. Al añadir un momento de fuerzas ${\vec {\tau }}=-\tau _{0}\,{\vec {k}}$, sólo hay que añadir este momento a la condición (3) de suma de momentos cero.

${\vec {M}}_{A}={\overrightarrow {OB}}\times {\vec {B}}+{\overrightarrow {OC}}\times {\vec {F}}_{0}+{\vec {\tau }}={\vec {0}}.\qquad (5)$

Esto modifica la ecuación (4), que queda

$-Bh+{\dfrac {1}{2}}F_{0}d-\tau _{0}=0.\qquad (6)$

Resolviendo las ecuaciones (1), (2) y (6) obtenemos

${\begin{array}{l}{\vec {A}}=-{\dfrac {F_{0}d-2\tau _{0}}{2h}}\,{\vec {\imath }}+F_{0}\,{\vec {\jmath }},\\{\vec {B}}={\dfrac {F_{0}d-2\tau _{0}}{2h}}\,{\vec {\imath }}.\end{array}}$

La condición para que la barra se separe en $B$ es que la normal sea nula o negativa (que no es físicamente posible). Es decir

${\vec {\tau }}_{0}\geq {\dfrac {1}{2}}F_{0}d.$

Aplicación a arcos románicos y góticos

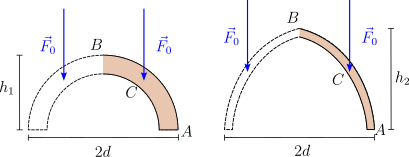
La figura debajo muestra un modelo muy simple de las fuerzas que actúan sobre la mitad de un arco románico, a la izquierda, y un arco gótico, a la derecha. La diferencia entre los dos es que el arco gótico es mas alto, para la misma abertura $d$. Como se ve en el cálculo previo, la fuerza de reacción $A_{x}$ es inversamente proporcional a la altura del arco. Entonces tenemos

$A_{1x}={\dfrac {F_{0}d}{2h_{1}}},\qquad A_{1x}={\dfrac {F_{0}d}{2h_{2}}}\Longrightarrow A_{2x}<A_{1x}.$

Entonces, la fuerza lateral que ejerce el arco en el apoyo $A$ es menor para el caso del gótico. Esta es la fuerza que debe soportar el muro en la que se apoya el arco. Por tanto, los muros de las iglesias góticas pueden ser mas delgados y, entonces, mas altos. Y ademas admiten ventanas mas grandes.