Segunda Prueba de Control 2017/18 (G.I.E.R.M.)

Aro con barra articulada

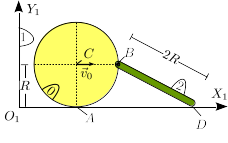
El disco de la figura (sólido "0"), de radio $R$, rueda sin deslizar sobre el eje $O_{1}X_{1}$. El centro del disco se mueve con rapidez constante $v_{0}$, como se indica en la figura. Una barra (sólido "2") de longitud $2R$ está articulada en el punto $B$ de la circunferencia exterior del disco. El otro extremo de la barra desliza sobre el eje $O_{1}X_{1}$.

1. Localiza gráficamente los C.I.R. de los movimientos {01}, {20} y {21} en el instante indicado en la figura. Explica el procedimiento seguido.
2. Encuentra reducciones cinemáticas de los tres movimientos relativos indicados.
3. Calcula ${\vec {\alpha }}_{21}$ y ${\vec {a}}_{21}^{\,D}$.

Partícula engarzada en un hilo circular con un muelle

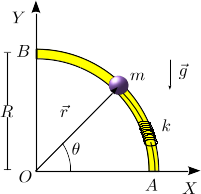
Una partícula de masa $m$ está engarzada en un aro de radio $R$. El contacto entre la partícula y el aro es liso. La partícula está conectada a un muelle de constante elástica $k$ y longitud natural nula. El otro extremo del muelle está anclado en el punto $A$. En el instante inicial la partícula se encuentra en el punto $A$ y se le comunica una velocidad vertical de módulo $v_{0}$.

1. Encuentra la expresión de la energía mecánica del muelle en todo instante.
2. Calcula el momento cinético de la partícula cuando $\theta =\pi /4$.
3. ¿Cuál es el valor mínimo de $v_{0}$ para que la partícula llegue hasta el punto $B$?

Nota: La energía potencial elástica del muelle tiene la expresión $U_{k}=kl^{2}/2$, siendo $l$ su longitud.

Onda estacionaria en una cuerda tensa

Una onda estacionaria en una cuerda horizontal de longitud 1.64 m oscila de modo que tiene dos nodos (sin contar los puntos extremos) cuando la frecuencia es de 120 Hz. En los antinodos la distancia entre el punto más alto y el más bajo que alcanza la cuerda es de 8.00 cm.

1. Escribe una función matemática que describa la onda estacionaria.
2. Escribe funciones matemáticas que describan las ondas de igual amplitud que viajan en sentidos contrarios y producen la onda estacionaria.
3. Si la densidad volumétrica de masa de la cuerda es $1.00\times 10^{-3}\,\mathrm {kg/m}$, calcula la tensión a la que está sometida la cuerda.