Primera Prueba de Control 2018/19 (G.I.C.)

Barra con traslación y rotación

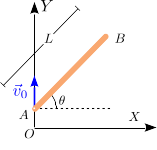
Una barra de longitud $L$ se mueve de modo que su extremo $A$ se desplaza sobre el eje $OY$ con velocidad uniforme $v_{0}$ y el ángulo que forma la barra con el eje $OX$ es $\theta =\omega _{0}t$. En el instante inicial el punto $A$ estaba en el origen y la barra estaba horizontal, es decir $\theta (0)=0$.

1. Escribe la expresión que da el vector de posición del punto $B$.
2. Encuentra la aceleración del punto $B$.
3. Si se cumple $L\omega _{0}={\sqrt {3}}v_{0}$, ¿cuánto vale la aceleración tangencial del punto $B$ en el instante $t=\pi /2\omega _{0}$?
4. En ese mismo instante, y con el mismo valor de $L\omega _{0}$, cuánto vale la curvatura de la trayectoria del punto $B$?

Masa colgando de cuerda y muelle

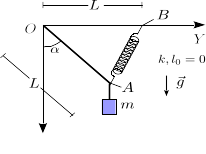
Una partícula de masa $m$ cuelga de una cuerda de longitud $L$ y un muelle de constante elástica $k$ y longitud natural nula, como se indica en la figura. El punto $B$ de anclaje del muelle está a una distancia $L$ del origen. Supondremos que la cuerda está tensa en todo momento.

1. Dibuja el diagrama de fuerzas que actúan sobre la masa $m$ y el punto $A$. Muestra correctamente la dirección y sentido de todas las fuerzas.
2. Escribe la expresión del vector ${\overrightarrow {BA}}$
3. Suponiendo que $mg=kL$, ¿cuál es el valor de $\alpha$ para el que hay equilibrio mecánico?
4. Para la situación de la pregunta anterior, ¿cuánto vale la tensión en la cuerda que une los puntos $O$ y $A$?

Masa en plano inclinado con muelle

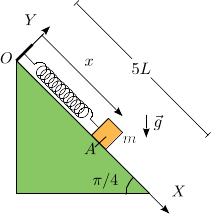
Una masa m está conectada a un muelle de constante elástica k y longitud natural nula. La masa puede deslizarse por un plano inclinado como se indica en la figura. El muelle se mantiene siem- pre paralelo a la superficie del plano inclinado. La gravedad actúa como se indica en el dibujo.

1. Si el contacto entre la masa y el plano es liso, ¿para que valor de x la masa está en equilibrio?
2. Teniendo en cuenta ahora el rozamiento y suponiendo que $mg={\sqrt {2}}kL$, ¿cuál es el rango de posiciones de equilibrio?