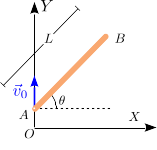
Enunciado Una barra de longitud
L
{\displaystyle L}
A
{\displaystyle A}
O
Y
{\displaystyle OY}
v
0
{\displaystyle v_{0}}
O
X
{\displaystyle OX}
θ
=
ω
0
t
{\displaystyle \theta =\omega _{0}t}
A
{\displaystyle A}
θ
(
0
)
=
0
{\displaystyle \theta (0)=0}
Escribe la expresión que da el vector de posición del punto
B
{\displaystyle B}
Encuentra la aceleración del punto
B
{\displaystyle B}
Si se cumple
L
ω
0
=
3
v
0
{\displaystyle L\omega _{0}={\sqrt {3}}v_{0}}
B
{\displaystyle B}
t
=
π
/
2
ω
0
{\displaystyle t=\pi /2\omega _{0}}
En ese mismo instante, y con el mismo valor de
L
ω
0
{\displaystyle L\omega _{0}}
B
{\displaystyle B}
Solución Vector de posición del punto
B
{\displaystyle B}
El vector de posición del punto
B
{\displaystyle B}
O
B
→
=
O
A
→
+
A
B
→
.
{\displaystyle {\overrightarrow {OB}}={\overrightarrow {OA}}+{\overrightarrow {AB}}.}
El punto
A
{\displaystyle A}
O
Y
{\displaystyle OY}
O
A
→
=
v
0
t
ȷ
→
.
{\displaystyle {\overrightarrow {OA}}=v_{0}t\,{\vec {\jmath }}.}
El otro vector es
A
B
→
=
L
cos
θ
ı
→
+
L
s
e
n
θ
ȷ
→
,
{\displaystyle {\overrightarrow {AB}}=L\cos \theta \,{\vec {\imath }}+L\,\mathrm {sen} \,\theta \,{\vec {\jmath }},}
donde, según el enunciado, tenemos
θ
=
ω
0
t
{\displaystyle \theta =\omega _{0}t}
O
B
→
=
L
cos
θ
ı
→
+
(
v
0
t
+
L
s
e
n
θ
)
ȷ
→
.
{\displaystyle {\overrightarrow {OB}}=L\cos \theta \,{\vec {\imath }}+(v_{0}t+L\,\mathrm {sen} \,\theta )\,{\vec {\jmath }}.}
Aceleración del punto
B
{\displaystyle B}
La velocidad del punto
B
{\displaystyle B}
v
→
B
=
d
O
B
→
d
t
=
−
L
θ
˙
s
e
n
θ
ı
→
+
(
v
0
+
L
θ
˙
cos
θ
)
ȷ
→
=
−
L
ω
0
s
e
n
θ
ı
→
+
(
v
0
+
L
ω
0
cos
θ
)
ȷ
→
.
{\displaystyle {\vec {v}}_{B}={\dfrac {\mathrm {d} {\overrightarrow {OB}}}{\mathrm {d} t}}=-L{\dot {\theta }}\,\mathrm {sen} \,\theta \,{\vec {\imath }}+(v_{0}+L{\dot {\theta }}\cos \theta )\,{\vec {\jmath }}=-L\omega _{0}\,\mathrm {sen} \,\theta \,{\vec {\imath }}+(v_{0}+L\omega _{0}\cos \theta )\,{\vec {\jmath }}.}
Hemos usado
θ
˙
=
ω
0
{\displaystyle {\dot {\theta }}=\omega _{0}}
a
→
B
=
d
v
→
B
d
t
=
−
L
ω
0
θ
˙
cos
θ
ı
→
−
L
ω
0
θ
˙
s
e
n
θ
ȷ
→
=
−
L
ω
0
2
cos
θ
ı
→
−
L
ω
0
2
s
e
n
θ
ȷ
→
{\displaystyle {\vec {a}}_{B}={\dfrac {\mathrm {d} {\vec {v}}_{B}}{\mathrm {d} t}}=-L\omega _{0}{\dot {\theta }}\cos \theta \,{\vec {\imath }}-L\omega _{0}{\dot {\theta }}\,\mathrm {sen} \,\theta \,{\vec {\jmath }}=-L\omega _{0}^{2}\cos \theta \,{\vec {\imath }}-L\omega _{0}^{2}\,\mathrm {sen} \,\theta \,{\vec {\jmath }}}
Aceleración tangencial y curvatura En el instante indicado,
t
=
π
/
2
ω
0
{\displaystyle t=\pi /2\omega _{0}}
θ
(
π
/
2
ω
0
)
=
π
/
2.
{\displaystyle \theta (\pi /2\omega _{0})=\pi /2.}
La velocidad y la aceleración en ese instante son
v
→
B
=
−
L
ω
0
ı
→
+
v
0
ȷ
→
,
a
→
B
=
−
L
ω
0
2
ȷ
→
.
{\displaystyle {\begin{array}{l}{\vec {v}}_{B}=-L\omega _{0}\,{\vec {\imath }}+v_{0}\,{\vec {\jmath }},\\{\vec {a}}_{B}=-L\omega _{0}^{2}\,{\vec {\jmath }}.\end{array}}}
El enunciado dice que consideremos la situación en que se cumple
L
ω
0
=
3
v
0
{\displaystyle L\omega _{0}={\sqrt {3}}v_{0}}
v
→
B
=
−
3
v
0
ı
→
+
v
0
ȷ
→
,
a
→
B
=
−
3
v
0
ω
0
ȷ
→
.
{\displaystyle {\begin{array}{l}{\vec {v}}_{B}=-{\sqrt {3}}v_{0}\,{\vec {\imath }}+v_{0}\,{\vec {\jmath }},\\{\vec {a}}_{B}=-{\sqrt {3}}v_{0}\omega _{0}\,{\vec {\jmath }}.\end{array}}}
El módulo de la velocidad es
|
v
→
B
|
=
3
v
0
2
+
v
0
2
=
2
v
0
.
{\displaystyle |{\vec {v}}_{B}|={\sqrt {3v_{0}^{2}+v_{0}^{2}}}=2v_{0}.}
La aceleración tangencial es
a
T
=
a
→
B
⋅
v
→
B
|
v
→
B
|
=
−
3
v
0
2
ω
0
2
v
0
=
−
3
v
0
ω
0
2
.
{\displaystyle a_{T}={\dfrac {{\vec {a}}_{B}\cdot {\vec {v}}_{B}}{|{\vec {v}}_{B}|}}={\dfrac {-{\sqrt {3}}v_{0}^{2}\omega _{0}}{2v_{0}}}=-{\dfrac {{\sqrt {3}}v_{0}\omega _{0}}{2}}.}
La aceleración normal en ese instante es
a
N
=
|
a
→
B
|
2
−
a
T
2
=
3
2
v
0
ω
0
.
{\displaystyle a_{N}={\sqrt {|{\vec {a}}_{B}|^{2}-a_{T}^{2}}}={\dfrac {3}{2}}v_{0}\omega _{0}.}
Por lo que la curvatura es
κ
=
a
N
|
v
→
B
|
2
=
3
ω
0
8
v
0
.
{\displaystyle \kappa ={\dfrac {a_{N}}{|{\vec {v}}_{B}|^{2}}}={\dfrac {3\omega _{0}}{8v_{0}}}.}