Primera Convocatoria 2016/17 (G.I.C.)

Dos bloques superpuestos conectados a un muelle

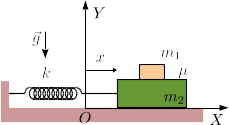
Un bloque de masa $m_{2}$ desliza sin rozamiento sobre una superficie horizontal. El bloque está conectado a un muelle de constante elástica $k$. El muelle se encuentra relajado cuando la coordenada $x$ de la figura es cero. Encima de este bloque se pone otro de masa $m_{1}$. El contacto entre los dos bloques es rugoso, caracterizado por un coeficiente de rozamiento estático $\mu$. Los bloques están sometidos a la acción de la gravedad.

1. Dibuja el diagrama de fuerzas de cada bloque. Exprésalas en el sistema de ejes de la figura.
2. Suponiendo que los dos bloques se mueven a la vez, encuentra la ecuación diferencial para $x(t)$, así como los valores de todas las fuerzas. (Pueden quedar en función de $x(t)$)
3. Si las condiciones iniciales son $x(0)=0$ y ${\dot {x}}(0)=v_{0}$, con $v_{0}$ una constante positiva, encuentra la posición y velocidad de los bloques en función del tiempo.
4. ¿Cuál es el valor máximo de $v_{0}$ para que el bloque de arriba no deslice respecto al de abajo?

Barra con muelle vertical y masa colgando

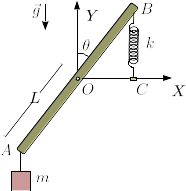
Una barra homogénea, de masa $m$ y longitud $2L$, está articulada en el origen de coordenadas en su punto medio, de modo que ese punto permanece fijo. De su extremo izquierda cuelga una masa $m$, conectada a la barra por un hilo inextensible y sin masa. El hilo se mantiene siempre vertical. El extremo derecho está conectado a un muelle ideal de constante elástica $k$ y longitud natural nula. El otro extremo del muelle se ancla en un pasador $C$, de modo que el muelle siempre permanece vertical. La gravedad actúa hacia abajo, como se indica en la figura.

1. Dibuja el diagrama de fuerzas que actúan sobre la barra.
2. Determina las posiciones de equilibrio de la barra, así como la expresión de la fuerza vincular que actúa sobre ella en cada una de las posiciones.
3. Supongamos que sustitiumos la masa en el extremo $A$ por una tuerca apretada en $O$, que ejerce un momento de fuerzas sobre la barra ${\vec {\tau }}=\tau _{0}\,{\vec {k}}$. ¿Cuánto vale $\theta$ en este caso en situación de equilibrio?
4. Partiendo de la situación descrita en 3, con la barra en reposo y con $\theta =\pi /4$, aflojamos completa y rápidamente la tuerca. ¿Cuánto vale la energía cinética de la barra y la rapidez del punto $B$ cuándo este está sobre el eje $OX$? (Dato: $I_{O}=mL^{2}/3$)

Partícula en aro con movimiento uniforme

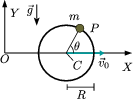
Una partícula se mueve sobre un aro de modo que su velocidad angular respecto al aro es ${\dot {\theta }}=\omega _{0}=\mathrm {cte}$. A su vez, el aro tiene un movimiento de traslación, de modo que su centro se mueve sobre el eje $OX$ con rapidez constante $v_{0}$. La gravedad actúa como se indica en la figura. En el instante inicial el centro del aro coincidía con el punto $O$ y la partícula estaba sobre el eje $OY$. Se cumple la condición $v_{0}>R\omega _{0}$.

1. Encuentra la expresión de los vectores posición y velocidad de la partícula en cualquier instante de tiempo.
2. Encuentra la fuerza que el aro ejerce sobre la partícula durante el movimiento, así como la potencia que aporta. ¿El contacto es liso? Razona la respuesta.
3. Calcula las componentes intrínsecas de la aceleración, así como el radio de curvatura de la trayectoria de la partícula, en el instante en que la partícula ha dado una vuelta completa al aro, empezando a contar desde $t=0$.