Barra con muelle vertical y masa colgando, Enero 2017 (G.I.C.)

Enunciado

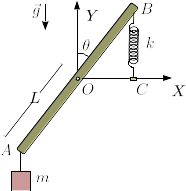
Una barra homogénea, de masa $m$ y longitud $2L$, está articulada en el origen de coordenadas en su punto medio, de modo que ese punto permanece fijo. De su extremo izquierda cuelga una masa $m$, conectada a la barra por un hilo inextensible y sin masa. El hilo se mantiene siempre vertical. El extremo derecho está conectado a un muelle ideal de constante elástica $k$ y longitud natural nula. El otro extremo del muelle se ancla en un pasador $C$, de modo que el muelle siempre permanece vertical. La gravedad actúa hacia abajo, como se indica en la figura.

1. Dibuja el diagrama de fuerzas que actúan sobre la barra.
2. Determina las posiciones de equilibrio de la barra, así como la expresión de la fuerza vincular que actúa sobre ella en cada una de las posiciones.
3. Supongamos que sustitiumos la masa en el extremo $A$ por una tuerca apretada en $O$, que ejerce un momento de fuerzas sobre la barra ${\vec {\tau }}=\tau _{0}\,{\vec {k}}$. ¿Cuánto vale $\theta$ en este caso en situación de equilibrio?
4. Partiendo de la situación descrita en 3, con la barra en reposo y con $\theta =\pi /4$, aflojamos completa y rápidamente la tuerca. ¿Cuánto vale la energía cinética de la barra y la rapidez del punto $B$ cuándo este está sobre el eje $OX$? (Dato: $I_{O}=mL^{2}/3$)

Solución

Diagrama de fuerzas

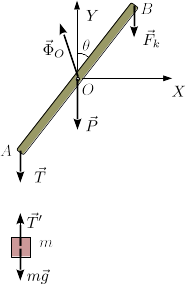
Las fuerzas que actúan sobre la barra son su peso, la del muelle, la que ejerce la cuerda en $A$ y la fuerza vincular en $O$

${\begin{array}{l}{\vec {P}}=-mg\,{\vec {\jmath }},\\{\vec {F}}_{k}=-kL\cos \theta \,{\vec {\jmath }},\\{\vec {\Phi }}^{O}=O_{x}\,{\vec {\imath }}+O_{y}\,{\vec {\jmath }},\\{\vec {T}}=-T\,{\vec {\jmath }}\end{array}}$

La fuerza vincular en $O$ tiene dos componentes porque los dos posibles movimientos del punto (vertical y horizontal) están prohibidos. Esta fuerza no tiene por qué ser perpendicular a la barra.

El valor de la tensión de la cuerda se obtiene de analizar el equilibrio de la masa colgando. Para esta, dado que es una partícula, la condición de equilibrio es que la suma de fuerzas sea nula

${\vec {T}}'+m{\vec {g}}={\vec {0}}\Longrightarrow {\vec {T}}'=-m{\vec {g}}.$

Dado que la cuerda es ideal tenemos

${\vec {T}}=-{\vec {T}}'=m{\vec {g}}=-mg\,{\vec {\jmath }}.$

Posiciones de equilibrio de la barra

La barra es un sólido rígido. Entonces la condición de equilibrio mecánico es que la fuerza externa neta sea nula y que el momento externo respecto de cualquier punto sea nulo.

De la fuerza neta nula obtenemos

${\vec {P}}+{\vec {\Phi }}^{O}+{\vec {F}}_{k}+{\vec {T}}={\vec {0}}\Longrightarrow \left\{{\begin{array}{lclr}(X)&\to &O_{x}=0,&(1)\\(Y)&\to &-mg+O_{y}-kL\cos \theta -mg=0.&(2)\end{array}}\right.$

Calculamos el momento respecto a $O$. Sólo ejercen momento la cuerda y el muelle. Tenemos

${\begin{array}{l}{\overrightarrow {OA}}\times {\vec {T}}=mgL\,\mathrm {sen} \,\theta \,{\vec {k}},\\{\overrightarrow {OB}}\times {\vec {F}}_{k}=-kL^{2}\,\mathrm {sen} \,\theta \cos \theta \,{\vec {k}}.\end{array}}$

La condición de momento neto nulo nos da

$mgL\,\mathrm {sen} \,\theta -kL^{2}\,\mathrm {sen} \,\theta \cos \theta =0.\qquad (3)$

La ecuación (3) nos da las posiciones de equilibrio. Tenemos tres situaciones posibles

${\begin{array}{l}\mathrm {sen} \,\theta =0\Longrightarrow \theta =0,\pi \\\cos \theta ={\dfrac {mg}{kL}}.\end{array}}$

Para cada una de las posiciones las ecuaciones (1) y (2) nos dan el valor de la fuerza vincular en $O$

${\begin{array}{lcl}\theta =0&\to &{\vec {\Phi }}^{O}=(2mg+kL)\,{\vec {\jmath }},\\\theta =\pi &\to &{\vec {\Phi }}^{O}=(2mg-kL)\,{\vec {\jmath }},\\\cos \theta ={\dfrac {mg}{kL}}&\to &{\vec {\Phi }}^{O}=3mg\,{\vec {\jmath }}\\\end{array}}$

Situación con una tuerca

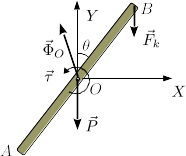
La imagen de la derecha muestra el diagrama de cuerpo libre en esta situación. Ya no está la cuerda, y la tuerca ejerce un momento ${\vec {\tau }}=\tau _{0}\,{\vec {k}}$, que es un dato. Las condiciones de equilibrio son las mismas, pero ahora las fuerzas y momentos ejercidos sobre la barra son

${\begin{array}{l}{\vec {P}}=-mg\,{\vec {\jmath }},\\{\vec {F}}_{k}=-kL\cos \theta \,{\vec {\jmath }},\\{\vec {\Phi }}^{O}=O_{x}\,{\vec {\imath }}+O_{y}\,{\vec {\jmath }},\\{\vec {\tau }}=\tau _{0}\,{\vec {k}}\end{array}}$

De la fuerza neta nula obtenemos

${\vec {P}}+{\vec {\Phi }}^{O}+{\vec {F}}_{k}={\vec {0}}\Longrightarrow \left\{{\begin{array}{lclr}(X)&\to &O_{x}=0,&(4)\\(Y)&\to &-mg+O_{y}-kL\cos \theta =0.&(5)\end{array}}\right.$

La condición de momento neto nulo nos da

${\vec {\tau }}+{\overrightarrow {OB}}\times {\vec {F}}_{k}={\vec {0}}\Longrightarrow \tau _{0}-kL^{2}\,\mathrm {sen} \,\theta \cos \theta =0.\qquad (6)$

Usando la relación

$\mathrm {sen} \,(2\theta )=2\,\mathrm {sen} \,\theta \cos \theta$

obtenemos para el ángulo de equilibrio

$\theta _{eq}={\dfrac {1}{2}}\,\mathrm {arcsen} \,\left({\dfrac {2\tau _{0}}{kL^{2}}}\right).$

Las ecuaciones (4) y (5) nos dan la fuerza vincular en situación de equilibrio.

Movimiento de la barra

Al soltar la tuerca, las única fuerza que hace trabajo, la del muelle, es conservativa. Entonces se conserva la energía mecánica. La energía potencial gravitatoria no cambia porque el centro de masas de la barra no cambia su altura. Justo al soltar la tuerca la energía potencial de la barra es

$U_{0}={\dfrac {1}{2}}k(L\cos \theta )^{2}\left.\right|_{\theta =\pi /4}={\dfrac {1}{4}}kL^{2}.$

y, dado que la barra parte del reposo, la energía mecánica inicial es

$E_{0}=U_{0}={\dfrac {1}{4}}kL^{2}.$

Cuando el punto $B$ está sobre el eje $OX$ el muelle está completamente contraído, por lo que la energía potencial elástica es nula. La energía mecánica es completamente cinética. Tenemos

$E_{1}=T_{1}={\dfrac {1}{2}}I_{O}\omega _{1}^{2}=E_{0}={\dfrac {1}{4}}kL^{2}.$

De aquí despejamos la velocidad de rotación en ese instante

$\omega _{1}={\sqrt {\dfrac {kL^{2}}{2I_{O}}}}={\sqrt {\dfrac {3k}{2m}}}.$

El punto $B$ realiza un movimiento circular de radio $L$, por lo que su rapidez en ese instante es

$v_{1}^{B}=\omega _{1}L=L{\sqrt {\dfrac {3k}{2m}}}.$

Errores comunes detectados en la corrección

1. Cada sólido o partícula sólo se ve afectado por las fuerzas que actúan directamente sobre él. Sobre la barra sólo actúan las fuerzas y pares que aparecen en los diagramas de cuerpo libre mostrados. La fuerza que ejerce el muelle sobre el eje $OX$ no es relevante. No se puede mezclar la fuerza que actúa la masa con las que actúan sobre la barra.
2. La fuerza de reacción vincular en $O$ no tiene por que ser perpendicular a la barra. Es una articulación, no un apoyo. Las dos componentes de esa fuerza son independientes entre sí. Toman el valor necesario para que el punto no se mueva sobre ninguno de los dos ejes.