Diferencia entre las páginas «Archivo:Particula plano dos muelles PPC 2015 enunciado.png» y «Semiaro con barra tangente, Noviembre 2015 (G.I.C.)»
Sin resumen de edición |
(Página creada con «== Enunciado == right El semiaro de la figura, de radio <math>R</math>, está articulado en <math>O</math>, de modo que rota alrededor de él. En el extremo <math>A</math> del seimaro se encuentra conectada una barra <math>AP</math>, de longitud <math>L</math>, que es siempre tangente al semiaro en <math>A</math>. El ángulo que forma la línea <math>OA</math> con el eje <math>OX</math> es <math>\theta(t)</math>…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | |||
[[Imagen:Semiaro_barra_tangente_enunciado_PPC_2015.png|right]] | |||
El semiaro de la figura, de radio <math>R</math>, está articulado en <math>O</math>, de modo que rota alrededor de él. En el extremo <math>A</math> del seimaro se encuentra conectada una barra <math>AP</math>, de longitud <math>L</math>, que es siempre tangente al semiaro en <math>A</math>. El ángulo que forma la línea <math>OA</math> con el eje <math>OX</math> es <math>\theta(t)</math>. | |||
#Escribe el vector de posición del punto <math>A</math> | |||
#Escribe el vector de posición del punto <math>P</math> | |||
#¿Cuál es el valor de <math>L</math> para que los puntos <math>O</math>, <math>B</math> y <math>P</math> estén alineados en todo instante? | |||
#La celeridad del punto <math>P</math> es <math>|\vec{v_P}|=v_0</math>, constante en el tiempo. Si en el instante inicial <math>\theta(0)=0</math>, ¿cómo es la ley horaria <math>\theta(t)</math>? | |||
#Supongamos ahora que la ley horaria es de la forma <math>\theta(t)=\omega_0t</math>, con <math>\omega_0</math> constante. Escribe el vector tangente en el instante inicial. | |||
#¿Cómo es el radio de curvatura de la trayectoria del punto <math>P</math> en todo instante? | |||
== Solución == | |||
=== Vectores de posición de los puntos <math>A </math> y <math>P </math>=== | |||
[[Imagen:Semiaro_barra_tangente_vectores_PPC_2015.png|right]] | |||
En la figura se indica donde aparece el ángulo <math>\theta </math>. El vector de posición del punto <math>A </math> es | |||
<center> | |||
<math> | |||
\overrightarrow{OA} = 2R\,\cos\theta\,\vec{\imath} + 2R\,\mathrm{sen}\,\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Construimos el vector <math>\overrightarrow{OP} </math> como la suma | |||
<center> | |||
<math> | |||
\overrightarrow{OP} = \overrightarrow{OA} + \overrightarrow{AP} | |||
</math> | |||
</center> | |||
Del dibujo vemos que | |||
<center> | |||
<math> | |||
\overrightarrow{AP} = L\,\mathrm{sen}\,\theta\,\vec{\imath} - L\cos\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Por tanto el vector pedido es | |||
<center> | |||
<math> | |||
\overrightarrow{OP} = (2R\cos\theta + L\,\mathrm{sen}\,\theta)\,\vec{\imath} + (2R\mathrm{sen}\,\theta - L\cos\theta)\,\vec{\jmath} | |||
</math> | |||
</center> | |||
=== Condición para que <math>O </math>, <math>B </math> y <math>P </math> estén siempre alineados === | |||
Para que esto ocurra debe cumplirse | |||
<center> | |||
<math> | |||
\overrightarrow{OB}\parallel \overrightarrow{OP} | |||
</math> | |||
</center> | |||
El vector de posición del punto <math>B </math> es <math>\overrightarrow{OB} = \overrightarrow{OC} + \overrightarrow{CB} </math>. Tenemos | |||
<center> | |||
<math> | |||
\overrightarrow{OC} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
y | |||
<center> | |||
<math> | |||
\overrightarrow{CB} = R\,\mathrm{sen}\,\theta\,\vec{\imath} - R\cos\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | |||
<math> | |||
\overrightarrow{OB} = (R\cos\theta + R\,\mathrm{sen}\,\theta)\,\vec{\imath} + (R\,\mathrm{sen}\theta - R\cos\theta)\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Para que los vectores <math>\overrightarrow{OP} </math> y <math>\overrightarrow{OB} </math> sean paralelos el ratio de sus componentes deben ser el mismo: | |||
<center> | |||
<math> | |||
\dfrac{2R\cos\theta + L\,\mathrm{sen}\,\theta}{R\cos\theta + R\,\mathrm{sen}\,\theta} | |||
= | |||
\dfrac{2R\mathrm{sen}\,\theta - L\cos\theta}{R\,\mathrm{sen}\theta - R\cos\theta} | |||
</math> | |||
</center> | |||
Esta condición también se puede obtener imponiendo la condición <math>\overrightarrow{OB}\times\overrightarrow{OP}=\vec{0} </math>. | |||
Aquí ya se puede ver que si <math>L=2R </math>, los numeradores son el doble de los denominadores, con lo que se cumple la condición. Si esto se nos pasa, proseguimos | |||
multiplicando en aspa | |||
<center> | |||
<math> | |||
2R^2\,\mathrm{sen}\,\theta\cos\theta - 2R^2\cos^2\theta + LR\,\mathrm{sen}^2\theta - LR\,\mathrm{sen}\,\theta\cos\theta = 2R^2\,\mathrm{sen}\,\theta\cos\theta - LR\cos^2\theta + 2R^2\,\mathrm{sen}^2\theta - LR\,\mathrm{sen}\,\theta\cos\theta | |||
</math> | |||
</center> | |||
Los términos con productos de senos y cosenos se van. Agrupando los otros y usando que <math>\cos^2\theta +\,\mathrm{sen}^2\theta=1</math> obtenemos | |||
<center> | |||
<math> | |||
LR = 2R^2 \Longrightarrow L = 2R. | |||
</math> | |||
</center> | |||
=== Ley horaria <math>\theta(t) </math>=== | |||
Ahora consideramos que el ángulo <math>\theta </math> es una función del tiempo <math>\theta(t) </math>. Derivamos el vector de posición <math>\overrightarrow{OP} </math> respecto del tiempo utilizando la regla de la cadena | |||
<center> | |||
<math> | |||
\vec{v}_P(t) = \dot{\overrightarrow{OP}} | |||
= | |||
\dfrac{\mathrm{d}\overrightarrow{OP}}{\mathrm{d}\theta}\dfrac{\mathrm{d}\theta}{\mathrm{d}t} | |||
= | |||
\dot{\theta}\,[(-2R\,\mathrm{sen}\,\theta+L\cos\theta)\,\vec{\imath} + (2R\cos\theta + L\,\mathrm{sen}\,\theta)\,\vec{\jmath}\,] | |||
</math> | |||
</center> | |||
Calculamos el módulo de este vector | |||
<center> | |||
<math> | |||
|\vec{v}_P| = \dot{\theta} \sqrt{4R^2\,\mathrm{sen}^2\theta + L^2\cos^2\theta - 2LR\cos\theta\,\mathrm{sen}\,\theta + 4R^2\cos^2\theta + L^2\,\mathrm{sen}^2\theta + 2LR\cos\theta\,\mathrm{sen}\,\theta} | |||
= | |||
\dot{\theta}\sqrt{4R^2+L^2} | |||
</math> | |||
</center> | |||
Igualamos este módulo a <math>v_0 </math>, con lo que obtenemos una ecuación diferencial para <math>\theta(t) </math> | |||
<center> | |||
<math> | |||
v_0 = \dot{\theta}\sqrt{4R^2+L^2} | |||
\Longrightarrow | |||
\dfrac{\mathrm{d}\theta}{\mathrm{d}t} = \dfrac{v_0}{\sqrt{4R^2+L^2}} | |||
</math> | |||
</center> | |||
Pasamos <math>\mathrm{d}t </math> a la derecha e integramos, imponiendo las condiciones iniciales en los límites de la integral | |||
<center> | |||
<math> | |||
\int\limits_0^{\theta(t)}\mathrm{d}\theta = \int\limits_0^t\dfrac{v_0}{\sqrt{4R^2+L^2}} | |||
\,\mathrm{d}t | |||
</math> | |||
</center> | |||
y obtenemos | |||
<center> | |||
<math> | |||
\theta(t) = \dfrac{v_0}{\sqrt{4R^2+L^2}}\,t | |||
</math> | |||
</center> | |||
=== Vector tangente en el instante inicial === | |||
El vector tangente puede calcularse a partir del vector velocidad | |||
<center> | |||
<math> | |||
\vec{T}(t) = \dfrac{\vec{v}_P(t)}{|\vec{v}_P|} | |||
</math> | |||
</center> | |||
Como nos lo piden en el instante inicial, usamos la condición inicial <math>\theta(0)=0 </math> para simplificar el vector velocidad | |||
<center> | |||
<math> | |||
\vec{v}_P(0) = \dot{\theta}(0)\,( L\,\vec{\imath} + 2R\,\vec{\jmath}) | |||
</math> | |||
</center> | |||
El módulo de este vector es | |||
<center> | |||
<math> | |||
|\vec{v}_P(0)| = \dot{\theta}(0)\sqrt{L^2+4R^2} | |||
</math> | |||
</center> | |||
Por tanto el vector tangente en <math>t=0 </math> es | |||
<center> | |||
<math> | |||
\vec{T}(0) = \dfrac{1}{\sqrt{L^2+4R^2}}\,\left(L\,\vec{\imath} + 2R\,\vec{\jmath}\right) | |||
</math> | |||
</center> | |||
=== Radio de curvatura === | |||
La distancia del punto <math>P </math> al punto <math>O </math> es siempre la misma, el módulo del vector <math>\overrightarrow{OP} </math>. Como además es una curva plana, pues está siempre en el plano <math>OXY </math>, la trayectoria es una circunferencia. El radio de curvatura es siempre el mismo e igual al radio de la circunferencia: | |||
<center> | |||
<math> | |||
R_{\kappa} = |\overrightarrow{OP}| = \sqrt{L^2 + 4R^2} | |||
</math> | |||
</center> | |||
[[Categoría:Cinemática del punto material|1]] | |||
[[Categoría:Problemas de examen]] | |||
Revisión actual - 10:29 3 nov 2023
Enunciado

El semiaro de la figura, de radio , está articulado en , de modo que rota alrededor de él. En el extremo del seimaro se encuentra conectada una barra , de longitud , que es siempre tangente al semiaro en . El ángulo que forma la línea con el eje es .
- Escribe el vector de posición del punto
- Escribe el vector de posición del punto
- ¿Cuál es el valor de para que los puntos , y estén alineados en todo instante?
- La celeridad del punto es , constante en el tiempo. Si en el instante inicial , ¿cómo es la ley horaria ?
- Supongamos ahora que la ley horaria es de la forma , con constante. Escribe el vector tangente en el instante inicial.
- ¿Cómo es el radio de curvatura de la trayectoria del punto en todo instante?
Solución
Vectores de posición de los puntos y
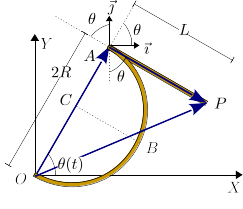
En la figura se indica donde aparece el ángulo . El vector de posición del punto es
Construimos el vector como la suma
Del dibujo vemos que
Por tanto el vector pedido es
Condición para que , y estén siempre alineados
Para que esto ocurra debe cumplirse
El vector de posición del punto es . Tenemos
y
Por tanto
Para que los vectores y sean paralelos el ratio de sus componentes deben ser el mismo:
Esta condición también se puede obtener imponiendo la condición . Aquí ya se puede ver que si , los numeradores son el doble de los denominadores, con lo que se cumple la condición. Si esto se nos pasa, proseguimos multiplicando en aspa
Los términos con productos de senos y cosenos se van. Agrupando los otros y usando que obtenemos
Ley horaria
Ahora consideramos que el ángulo es una función del tiempo . Derivamos el vector de posición respecto del tiempo utilizando la regla de la cadena
Calculamos el módulo de este vector
Igualamos este módulo a , con lo que obtenemos una ecuación diferencial para
Pasamos a la derecha e integramos, imponiendo las condiciones iniciales en los límites de la integral
y obtenemos
Vector tangente en el instante inicial
El vector tangente puede calcularse a partir del vector velocidad
Como nos lo piden en el instante inicial, usamos la condición inicial para simplificar el vector velocidad
El módulo de este vector es
Por tanto el vector tangente en es
Radio de curvatura
La distancia del punto al punto es siempre la misma, el módulo del vector . Como además es una curva plana, pues está siempre en el plano , la trayectoria es una circunferencia. El radio de curvatura es siempre el mismo e igual al radio de la circunferencia:
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 10:29 3 nov 2023 |  | 235 × 218 (21 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:
































![{\displaystyle {\vec {v}}_{P}(t)={\dot {\overrightarrow {OP}}}={\dfrac {\mathrm {d} {\overrightarrow {OP}}}{\mathrm {d} \theta }}{\dfrac {\mathrm {d} \theta }{\mathrm {d} t}}={\dot {\theta }}\,[(-2R\,\mathrm {sen} \,\theta +L\cos \theta )\,{\vec {\imath }}+(2R\cos \theta +L\,\mathrm {sen} \,\theta )\,{\vec {\jmath }}\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60a349824ed8dfbd533eb1ae21b0749cab8bbee8)












