Primera Prueba de Control 2015/16 (G.I.C.)

Partícula con movimiento rectilíneo y aceleración dependiente de x

Una partícula describe un movimiento rectilíneo, de modo que en todo instante su aceleración es $a=-k^{2}\,x$, siendo $k$ una constante. En el instante inicial se tiene $x(0)=0$, y $v(0)=v_{0}$, con $v_{0}>0$. El movimiento transcurre en el intervalo de tiempo $t\in [0,\pi /k]$.

1. Encuentra la velocidad de la partícula en función de su posición
2. ¿Cual es el valor de la celeridad al final del intervalo temporal?

Semiaro con barra tangente

El semiaro de la figura, de radio $R$, está articulado en $O$, de modo que rota alrededor de él. En el extremo $A$ del seimaro se encuentra conectada una barra $AP$, de longitud $L$, que es siempre tangente al semiaro en $A$. El ángulo que forma la línea $OA$ con el eje $OX$ es $\theta (t)$.

1. Escribe el vector de posición del punto $A$
2. Escribe el vector de posición del punto $P$
3. ¿Cuál es el valor de $L$ para que los puntos $O$, $B$ y $P$ estén alineados en todo instante?
4. La celeridad del punto $P$ es $|{\vec {v_{P}}}|=v_{0}$, constante en el tiempo. Si en el instante inicial $\theta (0)=0$, ¿cómo es la ley horaria $\theta (t)$?
5. Supongamos ahora que la ley horaria es de la forma $\theta (t)=\omega _{0}t$, con $\omega _{0}$ constante. Escribe el vector tangente en el instante inicial.
6. ¿Cómo es el radio de curvatura de la trayectoria del punto $P$ en todo instante?

Partícula sobre plano inclinado con dos muelles

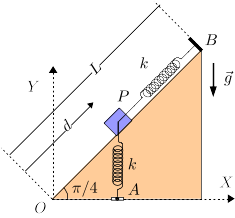
Una masa $m$ está obligada a permanecer sobre un plano horizontal que forma un ángulo $\pi /4$ con la horizontal. La masa está conectada a dos muelles con longitud natural nula y constante elástica $k$, anclados en los puntos $A$ y $B$ de la figura. El punto $A$ desliza sobre el eje $OX$ de modo que el muelle anclado en él permanece vertical en todo instante. El sistema está diseñado de modo que $mg=kL/{\sqrt {2}}$.

1. Encuentra la expresión vectorial de las fuerzas que ejercen los muelles, expresadas en los ejes de la figura
2. Suponiendo que todos los contactos son lisos, calcula la posición de equilibrio $d_{0}$
3. Añadimos ahora rozamiento entre la partícula y el plano. Dada una posición $d_{m}$, ¿cuánto vale el módulo de la fuerza de rozamiento?
4. Si el coeficiente de rozamiento estático es $\mu$, ¿cuál es el rango de posiciones posibles de equilibrio de la partícula?