Diferencia entre las páginas «Archivo:F1GIC-masa-plano-muelle-enunciado.png» y «Barra con traslación y rotación (Nov. 2018 G.I.C.)»
Sin resumen de edición |
(Página creada con «= Enunciado = right|250px Una barra de longitud <math>L</math> se mueve de modo que su extremo <math>A</math> se desplaza sobre el eje <math>OY</math> con velocidad uniforme <math>v_0</math> y el ángulo que forma la barra con el eje <math>OX</math> es <math>\theta=\omega_0 t</math>. En el instante inicial el punto <math>A</math> estaba en el origen y la barra estaba horizontal, es decir <math>\theta(0)=0</math>. # Escri…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Archivo:F1GIC-barra-rotando-enunciado.png|right|250px]] | |||
Una barra de longitud <math>L</math> se mueve de modo que su extremo <math>A</math> se desplaza sobre el eje <math>OY</math> con velocidad uniforme <math>v_0</math> y el ángulo que forma la barra con | |||
el eje <math>OX</math> es <math>\theta=\omega_0 t</math>. En el instante inicial el punto <math>A</math> estaba en el origen y la barra estaba horizontal, es decir <math>\theta(0)=0</math>. | |||
# Escribe la expresión que da el vector de posición del punto <math>B</math>. | |||
# Encuentra la aceleración del punto <math>B</math>. | |||
#Si se cumple <math>L\omega_0=\sqrt{3}v_0</math>, ¿cuánto vale la aceleración tangencial del punto <math>B</math> en el instante <math>t=\pi/2\omega_0</math>? | |||
#En ese mismo instante, y con el mismo valor de <math>L\omega_0</math>, cuánto vale la curvatura de la trayectoria del punto <math>B</math>? | |||
= Solución = | |||
== Vector de posición del punto <math>B</math> == | |||
El vector de posición del punto <math>B</math> puede escribirse como | |||
<center> | |||
<math> | |||
\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}. | |||
</math> | |||
</center> | |||
El punto <math>A</math> se mueve sobre el eje <math>OY</math> con velocidad uniforme. Si en el instante inicial estaba en el origen tenemos | |||
<center> | |||
<math> | |||
\overrightarrow{OA} = v_0t\,\vec{\jmath}. | |||
</math> | |||
</center> | |||
El otro vector es | |||
<center> | |||
<math> | |||
\overrightarrow{AB} = L\cos\theta\,\vec{\imath} + L\,\mathrm{sen}\,\theta\,\vec{\jmath}, | |||
</math> | |||
</center> | |||
donde, según el enunciado, tenemos <math>\theta=\omega_0 t</math>. Por tanto, el vector pedido es | |||
<center> | |||
<math> | |||
\overrightarrow{OB} = L\cos\theta\,\vec{\imath} + (v_0t + L\,\mathrm{sen}\,\theta)\,\vec{\jmath}. | |||
</math> | |||
</center> | |||
== Aceleración del punto <math>B</math> == | |||
La velocidad del punto <math>B</math> es | |||
<center> | |||
<math> | |||
\vec{v}_B = \dfrac{\mathrm{d}\overrightarrow{OB}}{\mathrm{d}t} = | |||
-L\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} + (v_0 + L\dot{\theta}\cos\theta)\,\vec{\jmath} | |||
= | |||
-L\omega_0\,\mathrm{sen}\,\theta\,\vec{\imath} + (v_0 + L\omega_0\cos\theta)\,\vec{\jmath}. | |||
</math> | |||
</center> | |||
Hemos usado <math>\dot{\theta}=\omega_0</math>. Derivamos otra vez respecto al tiempo para obtener la | |||
aceleración | |||
<center> | |||
<math> | |||
\vec{a}_B = \dfrac{\mathrm{d}\vec{v}_B}{\mathrm{d}t} = | |||
-L\omega_0\dot{\theta}\cos\theta\,\vec{\imath} - L\omega_0\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\jmath} | |||
= | |||
-L\omega_0^2\cos\theta\,\vec{\imath} - L\omega_0^2\,\mathrm{sen}\,\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
== Aceleración tangencial y curvatura == | |||
En el instante indicado, <math>t=\pi/2\omega_0</math>, tenemos | |||
<center> | |||
<math> | |||
\theta(\pi/2\omega_0) = \pi/2. | |||
</math> | |||
</center> | |||
La velocidad y la aceleración en ese instante son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{v}_B = -L\omega_0\,\vec{\imath} + v_0\,\vec{\jmath},\\ | |||
\vec{a}_B = -L\omega_0^2\,\vec{\jmath}. | |||
\end{array} | |||
</math> | |||
</center> | |||
El enunciado dice que consideremos la situación en que se cumple <math>L\omega_0=\sqrt{3}v_0</math>. Entonces | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{v}_B = -\sqrt{3}v_0\,\vec{\imath} + v_0\,\vec{\jmath},\\ | |||
\vec{a}_B = -\sqrt{3}v_0\omega_0\,\vec{\jmath}. | |||
\end{array} | |||
</math> | |||
</center> | |||
El módulo de la velocidad es | |||
<center> | |||
<math> | |||
|\vec{v}_B| = \sqrt{3v_0^2 + v_0^2} = 2v_0. | |||
</math> | |||
</center> | |||
La aceleración tangencial es | |||
<center> | |||
<math> | |||
a_T = \dfrac{\vec{a}_B\cdot\vec{v}_B}{|\vec{v}_B|} = \dfrac{-\sqrt{3}v_0^2\omega_0}{2v_0} = | |||
-\dfrac{\sqrt{3}v_0\omega_0}{2}. | |||
</math> | |||
</center> | |||
La aceleración normal en ese instante es | |||
<center> | |||
<math> | |||
a_N = \sqrt{|\vec{a}_B|^2-a_T^2} = \dfrac{3}{2}v_0\omega_0. | |||
</math> | |||
</center> | |||
Por lo que la curvatura es | |||
<center> | |||
<math> | |||
\kappa = \dfrac{a_N}{|\vec{v}_B|^2} = \dfrac{3\omega_0}{8v_0}. | |||
</math> | |||
</center> | |||
[[Categoría:Cinemática del punto material|1]] | |||
[[Categoría:Problemas de examen]] | |||
[[Categoría:Problemas de examen de F1 GIC]] | |||
Revisión actual - 10:52 3 nov 2023
Enunciado
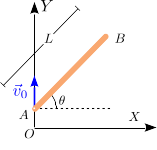
Una barra de longitud se mueve de modo que su extremo se desplaza sobre el eje con velocidad uniforme y el ángulo que forma la barra con el eje es . En el instante inicial el punto estaba en el origen y la barra estaba horizontal, es decir .
- Escribe la expresión que da el vector de posición del punto .
- Encuentra la aceleración del punto .
- Si se cumple , ¿cuánto vale la aceleración tangencial del punto en el instante ?
- En ese mismo instante, y con el mismo valor de , cuánto vale la curvatura de la trayectoria del punto ?
Solución
Vector de posición del punto
El vector de posición del punto puede escribirse como
El punto se mueve sobre el eje con velocidad uniforme. Si en el instante inicial estaba en el origen tenemos
El otro vector es
donde, según el enunciado, tenemos . Por tanto, el vector pedido es
Aceleración del punto
La velocidad del punto es
Hemos usado . Derivamos otra vez respecto al tiempo para obtener la aceleración
Aceleración tangencial y curvatura
En el instante indicado, , tenemos
La velocidad y la aceleración en ese instante son
El enunciado dice que consideremos la situación en que se cumple . Entonces
El módulo de la velocidad es
La aceleración tangencial es
La aceleración normal en ese instante es
Por lo que la curvatura es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 10:52 3 nov 2023 |  | 211 × 214 (14 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:
























