(Página creada con «= Enunciado = right En el sistema mostrado en la figura la masa <math>m_1</math> desliza sobre una superficie horizontal lisa. La masa <math>m_2</math> se mueve siempre sobre una línea vertical. Se cumple <math>m_1=m_2=m</math>. Ambas masas son tan pequeñas que pueden considerarse puntuales. El muelle tiene constante elástica <math>k=mg/L</math> y longitud natural nula. La longitud de la cuerda que une las masas…»)
 
(Página creada con «== Intercambio de posiciones en una barca == Una barca de longitud <math>2L</math> y masa <math>m_b=3m_0</math> está en reposo sobre el agua. En el extremo izquierdo de la barca se encuentra una persona de masa <math>m_1=2m_0</math>. En el extremo derecho hay otra persona de masa <math>m_2=m_0</math>. Las dos personas intercambian sus posiciones caminando sobre la barca hacia el extremo opuesto. Si se…»)
 
Línea 1: Línea 1:
= Enunciado =
==[[ Intercambio de posiciones en una barca (Ene. 2020 G.I.C.)| Intercambio de posiciones en una barca ]]==
[[File:F1-GIERM-Masas_muelle-energia-enunciado.png|right]]
En el sistema mostrado en la figura la masa <math>m_1</math> desliza sobre una superficie
horizontal lisa. La masa <math>m_2</math> se mueve siempre sobre una línea vertical. Se
cumple <math>m_1=m_2=m</math>. Ambas masas son tan pequeñas que pueden considerarse
puntuales. El muelle tiene constante elástica <math>k=mg/L</math> y longitud natural nula. La
longitud de la cuerda que une las masas es <math>2L</math>. En el instante inicial se
tiene <math>x_1=0</math>, de modo que la masa <math>m_2</math> está a la misma altura que la masa
<math>m_1</math>. En ese instante las masas están en reposo. En un primer
momento consideramos que la polea no tiene masa.
#Calcula la rapidez de la masa <math>m_2</math> cuando golpea el suelo.
#Ahora consideramos que el contacto entre la masa <math>m_1</math> y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico <math>\mu</math>. En esta situación, calcula la rapidez con que la masa <math>m_2</math> golpea el suelo. ¿Qué condición debe cumplir <math>\mu</math> para que la masa no llegue a impactar con el suelo?
#Supongamos ahora que la polea es un aro de masa <math>m</math> y radio <math>R</math>. El momento de inercia respecto un eje que pase por su centro  es <math>I=mR^2</math>. Consideramos de nuevo la situación sin rozamiento. Calcula en este caso, la rapidez de la masa <math>m_2</math> cuando golpea el suelo.


= Solución =
Una barca de longitud <math>2L</math> y masa <math>m_b=3m_0</math> está en reposo sobre el agua. En el
extremo izquierdo de la barca se encuentra una persona de masa <math>m_1=2m_0</math>. En
el extremo derecho hay otra persona de masa <math>m_2=m_0</math>. Las dos personas intercambian sus
posiciones caminando sobre la barca hacia el extremo opuesto. Si se desprecian las
fuerzas que ejerce el agua sobre la barca, ¿cuanto se ha desplazado la barca y hacia donde?


== Análisis con polea sin masa y sin rozamiento  ==
==[[ Partícula en semiaro circular con muelle (Ene. 2020 G.I.C.)| Partícula en semiaro circular con muelle]]==
Debido a que no hay rozamiento entre la masa <math>m_1</math> y la superficie plana la energía mecánica del sistema se conserva. La energía cinética es
[[File:F1GIERM-particula-aro-muelle-enunciado.png|right]]
<center>
Una partícula de masa <math>m</math> está engarzada en un semiaro de radio <math>R</math>. Un muelle de  
<math>
constante elástica <math>k=mg/R</math> y longitud natural nula conecta la partícula y el punto <math>A</math>
T = T_1 + T_2 = \dfrac{1}{2}mv_1^2 + \dfrac{1}{2}mv_2^2 = mv^2.
del semiaro. La gravedad actúa como se indica en la figura.  
</math>
</center>
Hemos usado que la rapidez de las dos masas es la misma. La energía potencial tiene contribución de la gravedad y del muelle. Tomamos como referencia de energía potencial gravitatoria la altura de la masa <math>m_1</math>En el instante inicial la energía mecánica es
<center>
<math>
T_i=U^g_i=U^k_i=0 \Longrightarrow E_i=0.
</math>
</center>
En el instante en que la masa <math>m_2</math> toca el suelo la energía mecánica es
<center>
<math>
\left.
\begin{array}{l}
T_f = mv_f^2\\
U^g_f = -mgL\\
U^k_f = kL^2/2 = mgL/2
\end{array}
\right\}
\Longrightarrow E_f = mv_f^2 - mgL/2.
</math>
</center>
Igualando las dos expresiones tenemos
<center>
<math>
E_i = E_f \Longrightarrow v_f = \sqrt{gL/2}.
</math>
</center>


== Análisis con polea sin masa y con rozamiento  ==
#Escribe los vectores de posición y velocidad de la partícula en la base vectorial cartesiana.
Las expresiones para la energía mecánica inicial y final son las mismas que en el apartado anterior. La
#Escribe la expresión que da la energía mecánica de la partícula para una posición arbitraria sobre el semiaro.
diferencia es que el rozamiento realiza trabajo sobre la masa <math>m_1</math>. Este trabajo es
#En el instante inicial, la partícula se encuentra en el punto <math>A</math>. Se le da un empujón de modo que su rapidez es <math>v_0</math>. Suponiendo que el contacto entre la partícula y el semiaro es liso, ¿cuanto debe valer <math>v_0</math> para que la partícula llegue hasta el punto <math>B</math>?
<center>
#Supongamos que el vínculo es rugoso. El trabajo que realiza el semiaro sobre la partícula es <math>|W_R|=\lambda mgR</math>, siendo <math>\lambda</math> una constante sin dimensiones.  ¿Cuál es el valor mínimo de <math>v_0</math> para repetir el apartado anterior?
<math>
W_r = \vec{F}_R\cdot\vec{d}_1 = -\mu mgL.
</math>
</center>
El balance de energía mecánica es
<center>
<math>
E_f - E_i = W_R
\Longrightarrow
mv_f^2 - mgL/2 = -\mu mgL
\Longrightarrow
v_f = \sqrt{\dfrac{gL}{2}}\,\sqrt{1-2\mu}.
</math>
</center>
La condición para que la masa <math>m_2</math> no llegue al suelo es que el radicando sea negativo
<center>
<math>
\mu>1/2.
</math>
</center>


== Análisis con polea con masa y sin rozamiento  ==
==[[ Partícula en semiaro circular con muelle: momento cinético (Ene. 2020 G.I.C.)| Movimiento de una partícula en semiaro circular con muelle usando el momento cinético]]==
La diferencia con el primer apartado es que hay que tener en cuenta la energía cinética de la polea. La energía mecánica inicial es nula de nuevo. La energía mecánica final es
[[File:F1GIERM-particula-aro-muelle-cinetico-enunciado.png|right]]
<center>
Una partícula de masa <math>m</math> está engarzada en un semiaro de radio <math>R</math>. Un muelle de
<math>
constante elástica <math>k=mg/R</math> y longitud natural nula conecta la partícula y el punto <math>A</math>
\left.
del semiaro. La gravedad no actúa.
\begin{array}{l}
#Dibuja el diagrama de fuerzas de la partícula.
T_f = mv_f^2 + I\omega_f^2/2 = mv_f^2 + mR^2(v_f/R)^2/2 = 3mgv_f^2/2. \\
#Escribe la expresión que da el momento cinético de la partícula respecto al punto <math>O</math>.
U^g_f = -mgL\\
#Aplicando el Teorema del Momento Cinético, encuentra la ecuación de movimiento de la partícula.
U^k_f = kL^2/2 = mgL/2
\end{array}
\right\}
\Longrightarrow E_f = \dfrac{3}{2}mv_f^2 - \dfrac{1}{2}mgL.
</math>
</center>
[[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]]
[[Categoría:Física I (G.I.E.R.M.)]]

Revisión actual - 14:43 31 oct 2023

Intercambio de posiciones en una barca

Una barca de longitud y masa está en reposo sobre el agua. En el extremo izquierdo de la barca se encuentra una persona de masa . En el extremo derecho hay otra persona de masa . Las dos personas intercambian sus posiciones caminando sobre la barca hacia el extremo opuesto. Si se desprecian las fuerzas que ejerce el agua sobre la barca, ¿cuanto se ha desplazado la barca y hacia donde?

Partícula en semiaro circular con muelle

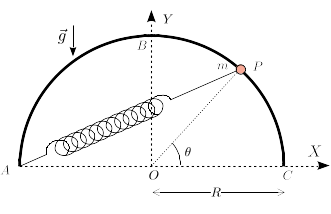
Una partícula de masa está engarzada en un semiaro de radio . Un muelle de constante elástica y longitud natural nula conecta la partícula y el punto del semiaro. La gravedad actúa como se indica en la figura.

  1. Escribe los vectores de posición y velocidad de la partícula en la base vectorial cartesiana.
  2. Escribe la expresión que da la energía mecánica de la partícula para una posición arbitraria sobre el semiaro.
  3. En el instante inicial, la partícula se encuentra en el punto . Se le da un empujón de modo que su rapidez es . Suponiendo que el contacto entre la partícula y el semiaro es liso, ¿cuanto debe valer para que la partícula llegue hasta el punto ?
  4. Supongamos que el vínculo es rugoso. El trabajo que realiza el semiaro sobre la partícula es , siendo una constante sin dimensiones. ¿Cuál es el valor mínimo de para repetir el apartado anterior?

Movimiento de una partícula en semiaro circular con muelle usando el momento cinético

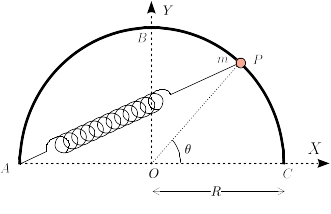
Una partícula de masa está engarzada en un semiaro de radio . Un muelle de constante elástica y longitud natural nula conecta la partícula y el punto del semiaro. La gravedad no actúa.

  1. Dibuja el diagrama de fuerzas de la partícula.
  2. Escribe la expresión que da el momento cinético de la partícula respecto al punto .
  3. Aplicando el Teorema del Momento Cinético, encuentra la ecuación de movimiento de la partícula.
Obtenido de «http://laplace.us.es/wiki/index.php?title=Masas_unidas_por_una_cuerda_con_muelle,_Enero_2020_(G.I.E.R.M.)&oldid=1262»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Masas_unidas_por_una_cuerda_con_muelle,_Enero_2020_(G.I.E.R.M.)&oldid=1262»