Primera Prueba de Control 2016/17 (MR G.I.C.)

Disco con barra articulada

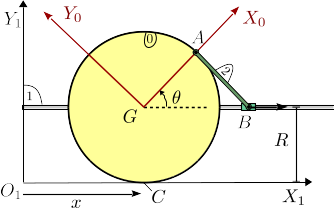
El disco de la figura (sólido "0"), de masa $m$ y radio $R$, rueda sin deslizar sobre el eje $OX_{1}$. Una barra (sólido "2"), de masa $m$ y longitud $R$, se encuentra articulada en el punto $A$ de la circunferencia del disco. El otro extremo, $B$ se conecta a un deslizador que se mueve sobre una barra paralela al eje $OX_{1}$. En el instante inicial los puntos $G$ y $A$ se encontraban sobre el eje $O_{1}Y_{1}$ (con el punto $A$ por encima del $G$).

1. Calcula la velocidad absoluta del punto $A$.
2. Determina la velocidad de rotación ${\vec {\omega }}_{20}$.
3. En esta pregunta y las siguientes suponemos que el punto $B$ se mueve con velocidad ${\vec {v}}=v_{0}\,{\vec {\imath }}_{1}$. Calcula el valor de ${\dot {\theta }}$.
4. Calcula el valor de ${\vec {\alpha }}_{21}$.
5. Determina el valor de ${\vec {v}}_{21}^{\,O_{1}}$ en el instante incial.
6. Calcula el momento cinético del disco respecto al punto de contacto con el suelo en el instante inicial.

Disco deslizando sobre hilo rotante

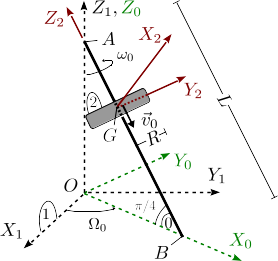
Un hilo rígido (sólido "0") de longitud $L$ rota alrededor del eje $OZ_{1}$ con velocidad angular constante $\Omega _{0}$, de modo que el punto $A$ está fijo y el punto $B$ describe una circunferencia sobre el plano $OX_{1}Y_{1}$. El hilo forma un ángulo $\pi /4$ con el plano $OX_{1}Y_{1}$. Un disco plano de masa $m$ y radio $R$ desliza por el hilo a la vez que rota alrededor de él con velocidad angular constante $\omega _{0}$. En el instante inicial el centro del disco estaba en el punto $A$. Se escoge un sólido "0" de modo que el plano $OX_{0}Z_{0}$ contiene siempre al hilo. El sistema "2", solidario con el disco, se escoge de modo que el eje $GZ_{2}$ coincide con su eje de simetría y el eje $GY_{2}$ es paralelo al eje $OY_{0}$. El punto $G$ del disco se mueve sobre el hilo con rapidez uniforme $v_{0}$, como se indica en la figura.

1. Calcula ${\vec {\omega }}_{21}$ y ${\vec {\alpha }}_{21}$.
2. Calcula la velocidad absoluta del punto $O_{1}$.
3. ¿Qué condición tiene que cumplirse para que el movimiento {21} sea una rotación pura en el instante inicial?
4. Supongamos que $\omega _{0}=0$. En este caso, el momento cinético del disco respecto de su centro de masas y su energía cinética en el instante en el que el punto $G$ está en el punto $B$.