Primera Prueba de Control 2017/18 (G.I.C.)

Partícula con cuerda deslizando sobre punto de una circunferencia

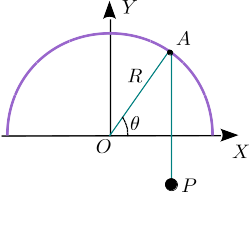
Una partícula de masa $m$ cuelga de una cuerda inextensible sin masa. La cuerda desliza sobre el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} . A su vez, este punto se mueve sobre una circunferencia de radio $R$. La longitud de la cuerda cambia en el tiempo según la ley Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle l(t) = 2R(1-\Omega t)} . En el instante inicial el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} se encontraba sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X} , a la derecha del origen.

1. Escribe vector de posición de la partícula
2. El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} realiza un movimiento circular uniforme con una aceleración que cumple Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle |\vec{a}_A| = 9R\Omega^2} . Encuentra la velocidad de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P} .
3. Calcula el vector normal de la trayectoria de la partícula y su curvatura en el instante $t=0$.

Partícula en hilo vertical con dos muelles

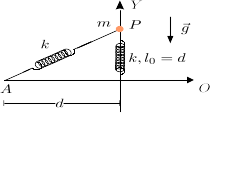
Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} puede moverse a lo largo del eje vertical $Y$. Está conectada a dos muelles como se indica en la figura. El muelle anclado en $A$ tiene constante elástica $k$ y longitud natural nula. El muelle anclado en $O$ tiene constante elástica $k$ y longitud natural $d$. El contacto entre la masa y el eje $Y$ es rugoso con coeficiente de rozamiento estático $\mu$. La partícula puede moverse a lo largo de todo el eje $Y$, por encima y por debajo del punto $O$.

1. Dibuja el esquema de cuerpo libre de la partícula, teniendo en cuenta el rozamiento, indicando de que fuerzas se conoce su sentido a priori y de cuales no.
2. Escribe las expresiones que dan las fuerzas de los muelles.
3. Encuentra la posición de equilibrio sin rozamiento.
4. Volviendo a considerar el rozamiento, y asumiendo que $mg=kd/2$, encuentra el rango de posiciones de equilibrio.
5. Considera de nuevo que no hay rozamiento. Ahora no hay ninguna condición sobre $mg$. ¿Cual es el período de las oscilaciones de la partícula?
6. Supongamos ahora que el sistema se ajusta de modo que $g=10.0\,\mathrm {m/s^{2}}$, $k=10.0\,\mathrm {N/m}$, $m=1.00\,\mathrm {kg}$, $d=1.00\,\mathrm {m}$. En el instante inicial la masa se suelta en reposo desde el punto $y=1.00\,\mathrm {m}$. ¿Cuál es la posición de la partícula en cada instante?

Masa deslizando verticalmente sobre otra masa con un muelle

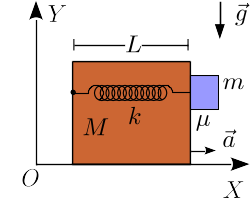
El bloque de masa $M$ y longitud $L$ de la figura se mueve hacia la derecha, con una aceleración constante ${\vec {a}}=a\,{\vec {\imath }}$. Un bloque pequeño de masa $m$ puede deslizar sobre la cara lateral del bloque grande. Un muelle horizontal, con constante elástica $k$ y longitud natural nula, está anclado en el lado izquierdo del bloque grande. El muelle se mantiene siempre horizontal. El contacto entre los dos bloques es rugoso, con un coeficiente de rozamiento estático $\mu =0.5$. ¿Para que valores de $a$ el bloque pequeño no desliza sobre el grande?