Diferencia entre revisiones de «Primera Prueba de Control 2020/21 (MR G.I.C.)»
(Página creada con «== Cilindro rodando sin deslizar == center Un cilindro de radio <math>R</math> (sólido "2") rueda sin deslizar sobre un plano fijo <math>O_1X_1Y_1Z_1</math> (sólido "1"). Los ejes <math>GX_2Y_2Z_2</math> son solidarios con el cilindro. Introducimos unos ejes auxiliares <math>GX_0Y_0Z_0</math> que cumplen las siguientes propiedades: el <math>X_0</math> es…») |
|||
| Línea 27: | Línea 27: | ||
#Calcula el momento de inercia respecto a un eje paralelo al eje <math>OX</math> y que pase por <math>A</math>. | #Calcula el momento de inercia respecto a un eje paralelo al eje <math>OX</math> y que pase por <math>A</math>. | ||
==[[ Movimiento instantáneo de barras | ==[[ Movimiento instantáneo de barras articuladas (Dic. 2020) | Movimiento instantáneo de barras articuladas ]]== | ||
[[Archivo:MRGIC-barrasCir-enunciado.png | right ]] | [[Archivo:MRGIC-barrasCir-enunciado.png | right ]] | ||
Una barra delgada (sólido “0”), de longitud <math>\sqrt{2}d</math>, está articulada en un punto fijo <math>O</math> y rota en el plano fijo <math>OX_1Y_1</math>. Otra barra delgada (sólido “2”) de la misma longitud se articula en su punto <math>B</math> en en el extremo de la barra “0”. El punto <math>A</math> de la barra “2” desliza sobre el eje <math>OY_1</math> con una velocidad <math>v_0</math> . Los cálculos que se piden a continuación corresponden al instante indicado en la figura. En ese instante las dos barras son perpendiculares. | Una barra delgada (sólido “0”), de longitud <math>\sqrt{2}d</math>, está articulada en un punto fijo <math>O</math> y rota en el plano fijo <math>OX_1Y_1</math>. Otra barra delgada (sólido “2”) de la misma longitud se articula en su punto <math>B</math> en en el extremo de la barra “0”. El punto <math>A</math> de la barra “2” desliza sobre el eje <math>OY_1</math> con una velocidad <math>v_0</math> . Los cálculos que se piden a continuación corresponden al instante indicado en la figura. En ese instante las dos barras son perpendiculares. | ||
Revisión actual - 11:18 11 oct 2024
Cilindro rodando sin deslizar
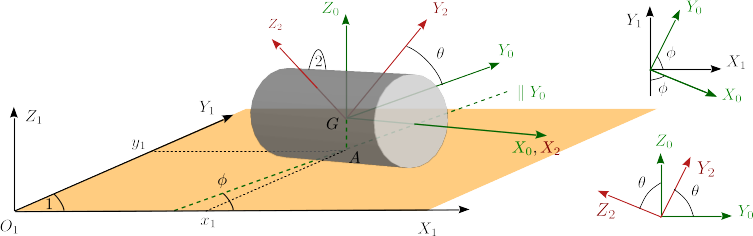
Un cilindro de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} (sólido "2") rueda sin deslizar sobre un plano fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O_1X_1Y_1Z_1} (sólido "1"). Los ejes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle GX_2Y_2Z_2} son solidarios con el cilindro. Introducimos unos ejes auxiliares Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle GX_0Y_0Z_0} que cumplen las siguientes propiedades: el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X_0} es paralelo al eje del cilindro; el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Z_0} es perpendicular al plano fijo "1"; el ángulo que forma el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y_0} con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X_1} es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \phi} . El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} señala el punto geométrico en la vertical de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} donde el cilindro está en contacto con el plano. Las coordenadas de este punto en los ejes "1" son Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_1} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y_1} . Estas son también las coordenadas de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} en el plano fijo. Los diagramas auxiliares indican los ángulos relevantes entre los diferentes sistemas de ejes.
- Encuentra la reducción cinemática en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} de los movimientos {01}, {20}, {21}. Expresa los resultados en la base "0" y usa el menor número de coordenadas posible.
2. Si el tensor de inercia del cilindro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} es de la forma
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overleftrightarrow{I_O} = \left[ \begin{array}{ccc} I_{1} & 0 & 0 \\ 0 & I_{2} & 0 \\ 0 & 0 & I_{2} \end{array} \right] }
con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_1} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_2} conocidos, calcula el momento cinético del cilindro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle G} y su energía cinética.
Tensor de inercia de un hexágono
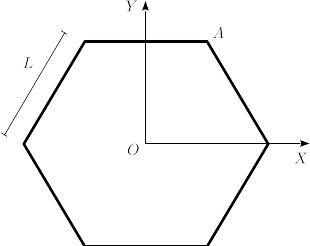
EL sólido rígido de la figura es un hexágono de lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle L} . Cada lado del hexágono tiene una masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m} .
- Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura..
- Calcula el tensor de inercia en el vértice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} , expresado en los mismos ejes.
- Calcula el momento de inercia respecto a un eje paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX} y que pase por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} .
Movimiento instantáneo de barras articuladas

Una barra delgada (sólido “0”), de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt{2}d} , está articulada en un punto fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} y rota en el plano fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1} . Otra barra delgada (sólido “2”) de la misma longitud se articula en su punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} en en el extremo de la barra “0”. El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} de la barra “2” desliza sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY_1} con una velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0} . Los cálculos que se piden a continuación corresponden al instante indicado en la figura. En ese instante las dos barras son perpendiculares.
- Determina gráfica y analíticamente la posición de los C.I.R. de los movimientos {01}, {20} y {21}
- Calcula una reducción cinemática de esos movimientos.
- Si la velocidad absoluta del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} es constante en el tiempo, calcula las derivadas temporales de esas reducciones cinemáticas.